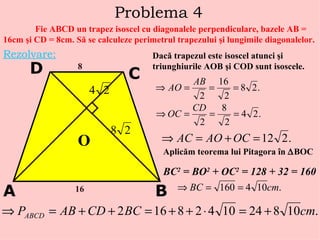
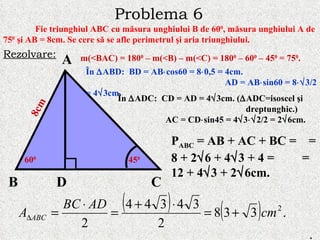
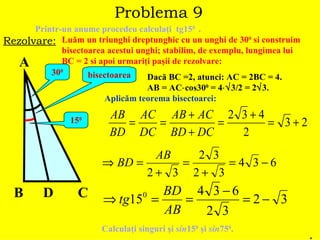
Documentul prezintă rezolvarea unor probleme de geometrie în triunghiuri, trapeze și pătrate, folosind teoreme precum teorema lui Pitagora și teorema cosinusului. Fiecare problemă include calcule detaliate pentru a determina lungimi, arii și perimetre ale figurilor geometrice menționate. Aceasta constituie o resursă educativă pentru elevii de clasa a V-a care studiază relațiile metrice în triunghiurile dreptunghice.

1. RELA ŢII METRICE ÎN TRIUNGHIUL DREPTUNGHIC PROBLEME REZOLVATE C lasa a VII-a .

2. P roblema 1 Fie triunghiul ABC dreptunghic î n A , AB = 10cm ş i AD = 5  3cm, AD  BC. Afla ţ i lungimea lui BD, BC ş i AC. Rezolva r e: A B C D 10cm 5  3cm 1) Aplic ă m teorema lui Pitagora î n  ABD pentru a afla BD: BD 2 = AB 2 – AD 2  BD 2 = 100 – 75 = 25  BD =  25 = 5 c m . 5cm 2) Aplic ă m teorema catetei (pentru cateta AB) pentru a afla BC: AB 2 = BD  BC  100 = 5  BC  BC = 100:5 = 20cm. 20cm 3) Pentru a afla lungimea catetei AC aplic ă m teorema lui Pitagora î n  ABC: AC 2 = BC 2 – AB 2  AC 2 = 400 – 100 = 300  AC =  100 = 10  3cm. 10  3cm Pentru consolidarea tehnicii de rezolvare a unui triunghi dreptunghic, î ncercati s ă rezolva ţ i problema aplic â nd ş i teorema î nal ţ imii. .

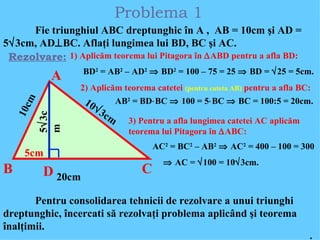
3. Fie ABCD un p ă trat de latur ă AB = 10cm; punctul E se afl ă î n interiorul p ă tratului astfel î ncat  AEB s ă fie echilateral. Afla ţ i lungimea lui [EC]. Rezolvare: Problema 2 A B C D E Construim perpendiculara FG pe AB ce trece prin E. F G Î n  EGB avem: BE=10cm, BG=5cm. 10 5 GE 2 = BE 2 – BG 2  GE 2 = 100-25=75 5  3 FE = GF – GE = 10 - 5  3cm. Î n  CEF: CE 2 = FE 2 + FC 2 .

4. Fie ABCD un paralelogram cu AB = 10cm, AD = 2  5cm ş i DE = 4cm , unde DE  AB . Afla ţ i lungimile celor dou ă diagonale. Rezolvare: Problema 3 A B C D E 2  5 10 4 Î n  ADE afl ă m pe AE: AE 2 = AD 2 – DE 2 = 20 – 16 = 4. AE =  4 = 2cm. 2  BE = AB – AE = 10 – 2 = 8cm. 8 Î n  BDE afl ă m pe BD: BD 2 = BE 2 + AD 2 = 64 + 16 = 80.  BD =  80 = 4  5cm. Cobor â m o perpendicular ă din C pe dreapta AB: F BF = AE = 2cm. 2 CF = DE = 4cm. 4 Î n  ACF avem: AC 2 = AF 2 + CF 2 = 12 2 + 4 2 = 144+16=160. .

5. Problema 4 Fie ABCD un trapez isoscel cu diagonalele perpendiculare, bazele AB = 16cm ş i CD = 8cm. S ă se calculeze perimetrul trapezului ş i lungimile diagonalelor. Rezolvare: A B C D 16 8 O Dac ă trapezul este isoscel atunci ş i triunghiurile AOB ş i COD sunt isoscele. Aplic ă m teorema lui Pitagora î n  BOC BC 2 = BO 2 + OC 2 = 128 + 32 = 160 .

6. Fie un triunghi cu lungimile a doua laturi a si b si m ă sura unghiului cuprins î ntre ele egal ă cu  . S ă se afle lungimea celei de-a treia laturi. Rezolvare: Problema 5 a b  Construim î nal ţ imea pe latura de lungime b . O notam cu h . h Î n triunghiul din st â nga avem: h = a  sin  ş i x = a  cos  x y c Î nseamn ă c ă y = b – x = b - a  cos  Aplic ă m teorema lui Pitagora î n triunghiul din dreapta: c 2 = h 2 + y 2 = (a  sin  ) 2 + (b - a  cos  ) 2 c 2 = a 2 sin 2  + b 2 – 2ab  cos  + a 2 cos 2  c 2 = a 2 (sin 2  + cos 2  )+b 2 – 2ab  cos  Dar sin 2  + cos 2  = 1, a ş adar  ( Teorema lui Pitagora generalizat ă sau teorema cosinusului ) . c 2 = a 2 + b 2 – 2ab  cos 

7. Problema 6 Fie triunghiul ABC cu m ă sura unghiului B de 60 0 , m ă sura unghiului A de 75 0 ş i AB = 8cm. Se cere s ă se afle perimetrul ş i aria triunghiului. Rezolvare: A B C 60 0 45 0 8cm m(<BAC) = 180 0 – m(<B) – m(<C) = 180 0 – 60 0 – 45 0 = 75 0 . D Î n  ABD: BD = AB  cos60 = 8  0,5 = 4cm. AD = AB  sin60 = 8  3/2 = 4  3cm. Î n  ADC: CD = AD = 4  3cm. (  ADC=isoscel ş i dreptunghic.) AC = CD  sin45 = 4  3  2/2 = 2  6cm. P ABC = AB + AC + BC = = 8 + 2  6 + 4  3 + 4 = = 12 + 4  3 + 2  6cm. .

8. Problema 7 Trapezul ABCD cu baza mic ă CD = 3cm are AD = 4cm ş i m ă sura unghiului A de 60 0 , iar m ă sura unghiului B de 30 0 . Se cere s ă se calculeze perimetrul ş i aria trapezului. Rezolvare: A B C D 4cm 3cm 8cm 60 0 30 0 E F AE = AD cos 60 = 4  0,5 = 2cm. DE = CF = AD sin 60 = 4  3/2 = 2  3cm. BC = CF:sin30 = 2  3/0,5 = 4  3cm. BF = BC cos 30=4  3  3/2=6cm. EF = CD = 3cm. .

9. Problema 8 Fie triunghiul ABC cu AB = c = 7cm, BC = a = 9cm ş i AC = b = 8cm. S ă se afle sinA, sinB si sinC. Rezolvare: A B C 7cm 9cm 8cm Folosim urm ă toarea formul ă de calcul a ariei unui triunghi: u nde p = semiperimetrul triunghiului. p = (a+b+c):2 = (7+8+9):2 = 12 Folosim alt ă formul ă de calcul a ariei unui triunghi: Analog vom calcula la fel si sin B sau sin C. Se poate aplica î n continuare si teorema sinusului: .

10. Problema 9 Printr-un anume procedeu calcula ţ i tg15 0 . Rezolvare: Lu ă m un triunghi dreptunghic cu un unghi de 30 0 si construim bisectoarea acestui unghi; stabilim, de exemplu, lungimea lui BC = 2 si apoi urmari ţ i pa ş ii de rezolvare: A B C 30 0 D bisectoarea 15 0 Dac ă BC =2, atunci: AC = 2BC = 4. AB = AC  cos30 0 = 4  3/2 = 2  3. Aplic ă m teorema bisectoarei: . Calcula ţ i singuri ş i sin 15 0 ş i sin 75 0 .

11. Problema 10 Far ă a utiliza tabele trigonometrice, calcula ţ i sin 75 0 . Rezolvare: Construim un triunghi cu unghiurile de 75 0 , 45 0 ş i 60 0 . A B C 7 5 0 45 0 60 0 D Not ă m BD = 1 1 Rezult ă : AB = 2; AD =  3; CD =  3; AC =  6. 2  3  3  6 Aria triunghiului ABC: Dar aria  ABC cu formula sinusului este: A ş adar avem: .