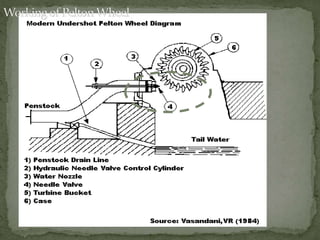
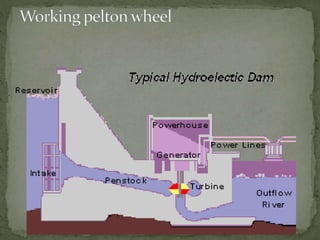
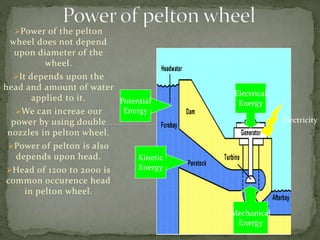
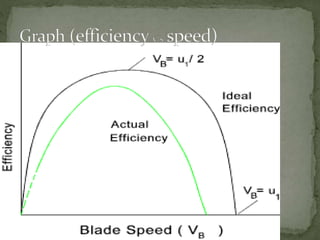
This document discusses the Pelton wheel, an impulse turbine invented in 1878. It is efficient at high heads, often over 90%. It works by having jets of water strike buckets on the rim of the wheel, transferring kinetic energy to rotate the shaft. The power produced depends on head and flow rate of water, not the diameter of the wheel. Double nozzles can increase power output. Maximum efficiency occurs when the water exits the buckets at half the inlet velocity.

2. Name Roll
 Waqas 10-MCT-19
 Shaheryar 10-MCT-57
 Usama 10-MCT-63
 Ishtiaq 10-MCT-64
 M.Ehsan 10-MCT-66

3. Pelton Wheel is the only
impulse turbine, named in
honour of L.A. Pelton (1829-
1908) of California, USA.
It was invented in 1878.
It is an efficient turbine
particularly suited to high
heads with efficiencies often
more than 90%.
Single nozzle impulse
turbines have a flat efficiency
curve and may be operated
down to loads of 20% of rated

4. The water flows along the
tangent to the path of the
runner.
When the water-jet contacts
the bucket, the water exerts
pressure on the bucket and
the water is decelerated as it
does a "u-turn" and flows out
the other side of the bucket at
low velocity.
A very small percentage of
the water's original kinetic
energy will still remain in the
water; however, this allows the
bucket to be emptied at the
same rate it is filled

7. *Work done is a parameter of physical
performance.
Work done by a pelton wheel per second
is determined,using torque(T) revolving
the wheel and the angular
displacement(d) in radian per second and
is given by:
Work=T*d
d is the angle between the whirl flow
direction and the vane.Torque is
calculated by angular velocity measured
by TachoMeter in RPM

9. Power of the pelton
wheel does not depend
upon diameter of the
wheel.
It depends upon the
head and amount of water
applied to it.
We can increae our
power by using double
nozzles in pelton wheel.
Power of pelton is also
depends upon head.
Head of 1200 to 2000 is
common occurence head
in pelton wheel.
Potential
Energy
Kinetic
Energy
Electrical
Energy
Mechanical
Energy
Electricity

10. The power P = Fu = Tω, where ω is
the angular velocity of the wheel.
 Substituting for F, we have P = 2ρQ(Vi − u)u.
 To find the runner speed at maximum
power, take the derivative of P with respect
to u and set it equal to zero, [dP/du = 2ρQ(Vi −
2u)].
 Maximum power occurs
whenu = Vi /2. Pmax = ρQVi
2/2.
Substituting the initial jet power Vi = √(2gh),
this simplifies to Pmax = ρghQ.
This quantity exactly equals the kinetic
power of the jet, so in this ideal case, the
efficiency is 100%, since all the energy in the
jet is converted to shaft output.

11. A wheel power divided by the
initial jet power, is the turbine
efficiency.
 η = 4u(Vi − u)/Vi
2.
It is zero for u = 0 and for u = Vi.
 As the equations indicate, when
a real Pelton wheel is working close
to maximum efficiency, the fluid
flows off the wheel with very little
residual velocity.
 This basic theory
does not suggest that efficiency
will vary with hydraulic head.

15. The work done /s by unit weight of water striking/s is given
by:
Work=1/g[(Vw1+Vw2)u]
Where
g is gravitational acceleration;
Vw1 is velocity of whirl at inlet;
Vw2 is velocity of whirl at outlet and
u is tangential velocity of vane or bucket.