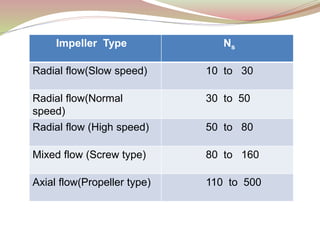
The document discusses unit specific quantities for turbines, including unit speed, power, and discharge under a unit head of 1m. It explains how these quantities can predict turbine performance under varying conditions and emphasizes the significance of specific speed for characterizing turbo machinery and selecting appropriate pumps or turbines. Additionally, it describes how the behavior and performance of geometrically similar turbines can be analyzed using specific speed across different turbine types.

1. UNIT AND
SPECIFIC
QUANTITY

2. In order to predict the behavior of a turbine working under
varying conditions of head, speed, and power, recourse
has been made to the concept and unit
The unit quantities give the speed, discharge and power
for a particular turbine under a head of 1m assuming the
same efficiency. The following are the three unit specific
quantities

3. Unit speed
Unit power
Unit discharge
Unit speed (Nu): The speed of the turbine, working
under unit head (say 1m) is known as
unit speed of the turbine. The tangential velocity is
given by,
u= πDN/60 or N=60u/πD
If H=1; then N=Nu√H
Where, H = head of water, under which the turbine is
working; N= speed of turbine under a head, H; u=
tangential velocity; Nu= speed of the turbine under a
unit head.

4. Unit Power Pu: The power developed by a turbine, working
under a unit head (say 1m)is known as unit power of the turbine.
Power developed by a turbine is given as, P=γQH and V=√2gH
P=γ(a√2gH)H
P=K2H3/2
IF , H=1; then ,P=Pu
Pu =k213/2≈k2
P=PuH3/2
Pu=P/H3/2
Unit discharge (Qu): The discharge of the turbine working
under a unit head (say 1m) is known as unit discharge
Q=a√2gH=k3√H
IF ,H=1 ; Then ,Q=Qu ;
Qu=k3√1=k3
Or , Q=Qu√H

5. Thus ,Qu=Q/√H
If a turbine is working under different heads, the behavior of
the turbine can be easily known from the unit quantities.
Nu=N1/√H1=N2/√H2
Pu=P1/H1
3/2=P2/H2
3/2
Qu=Q1/√H1=Q2/√H2
Where H1, H2 are the heads under which a turbine works;
N1,N2 are the corresponding speeds; Q1,Q2 are the
discharges, and P1,P2 are the power developed by the
turbine
The concept of the specific turbine is useful for comparing the
turbines of different types. The performance of turbines under
unit head gives us the comparison of turbines of the same type.

6. Specific speed Ns, is used to characterize turbo machinery
speed. Common commercial and industrial practices use
dimensioned versions which are of equal utility. Specific speed is
most commonly used in pump applications to define the suction
specific speed ,a quasi non-dimensional number that categorizes
pump impellers as to their type and proportions. In Imperial units it
is defined as the speed in revolutions per minute at which a
geometrically similar impeller would operate if it were of such a
size as to deliver one gallon per minute against one foot of
hydraulic head. In metric units flow may be in l/s or m³/s and head
in m, and care must be taken to state the units used.

7. Specific speed is an index used to predict desired pump or turbine
performance. i.e. it predicts the general shape of a pumps
impeller. It is this impeller's "shape" that predicts its flow and head
characteristics so that the designer can then select a pump or
turbine most appropriate for a particular application. Once the
desired specific speed is known, basic dimensions of the unit's
components can be easily calculated.
Several mathematical definitions of specific speed (all of them
actually ideal-device-specific) have been created for different
devices and applications

8. Specific speed(Ns): The speed geometrically similarly pump
when delivery 1m3/s against a head of 1m
The significance of Ns the performance & dimensional
proportions of pump having the same specific speed will be
the same even through their outside diameters & actual
operating speeds may be different
V=πDN
N1D1=N2D2
Ns=N√H/H3/2
N:- Actual speed of pump in RPM
Q:- Discharge m3/s
H:- Delivery ( or Manometric or gross ) head in m.

9. Let N be the actual speed of the pump therefore linear or
peripheral velocity at inlet will be
u1 =πD1N/60 = u1αD1N ----1
& u1 =√2gH = u1α √H--------2
From eq 1 & 2 , we get D1Nα√H or D1α√H/N----3
Further , Q = a1u1= π/4D1
2u1=π/4D1
2√2gH
Q α D1
2√H-----4
Substituting for D1 in eq 4 from 3 ,we get
Q α (√H/N)2 X √H = Q α H1/2/N2= Nα(√H3/2/Q
N=Ns X(H3/4/√Q)
Ns=N√Q/H3/4

10. Impeller Type Ns
Radial flow(Slow speed) 10 to 30
Radial flow(Normal
speed)
30 to 50
Radial flow (High speed) 50 to 80
Mixed flow (Screw type) 80 to 160
Axial flow(Propeller type) 110 to 500

11. A specific turbine is an imaginary turbine identical (identical in
shape, geometrical proportions, blade angles, gate openings,
etc.,) with actual turbine, but reduced to such a size that it
develops one kW power under unit head
The actual turbine under unit condition and specific turbine
both work under unit head(1m head), whatever the velocity
triangle holds good for the actual turbine, will hold good for
specific turbine also. In other words,
us=uu; Vfs=Vfu ; etc
Similarly , Qu=πDBVfu & Qs=πDsBsVfs
therefore , Qu/Qs=(D/Ds)2
Because, B=nD; Bs=nDS
Pu=γQuX1Xη0 ; Ps=γQsX1Xη0
Asumming overall efficiency to be same ,then ,

12. Pu/Ps=Qu/Qs=(D/Ds)2
The power of geometrically similar turbines working under
the same head vary as the square of the runner diameters.
Since, the specific turbine develops 1kW under a unit
head, Ps=1, therefore,
Pu=(D/Ds)2
Ds=D/√Pu
But Pu=P/H3/2
Therefore ,Ds = D/(√P/H3/2)
Further ,uu=πDNu/60 ,& us= πDsNs/60
Or ,Ns=NuD/Ds=Nu √P

13. But Nu=N/ √H
Thus ,Ns=N √(P)/H5/4
This value of Ns, the speed of the specific turbine is known as
specific speed of the turbine .
Turbine Maximum value of specific speed
Pelton wheel 43 to 60.9
Francis turbine (slow runner)
Francis turbine (fast runner)
45.78
316 approximately
Kaplan turbine 878 approximately

14. THANK
YOU