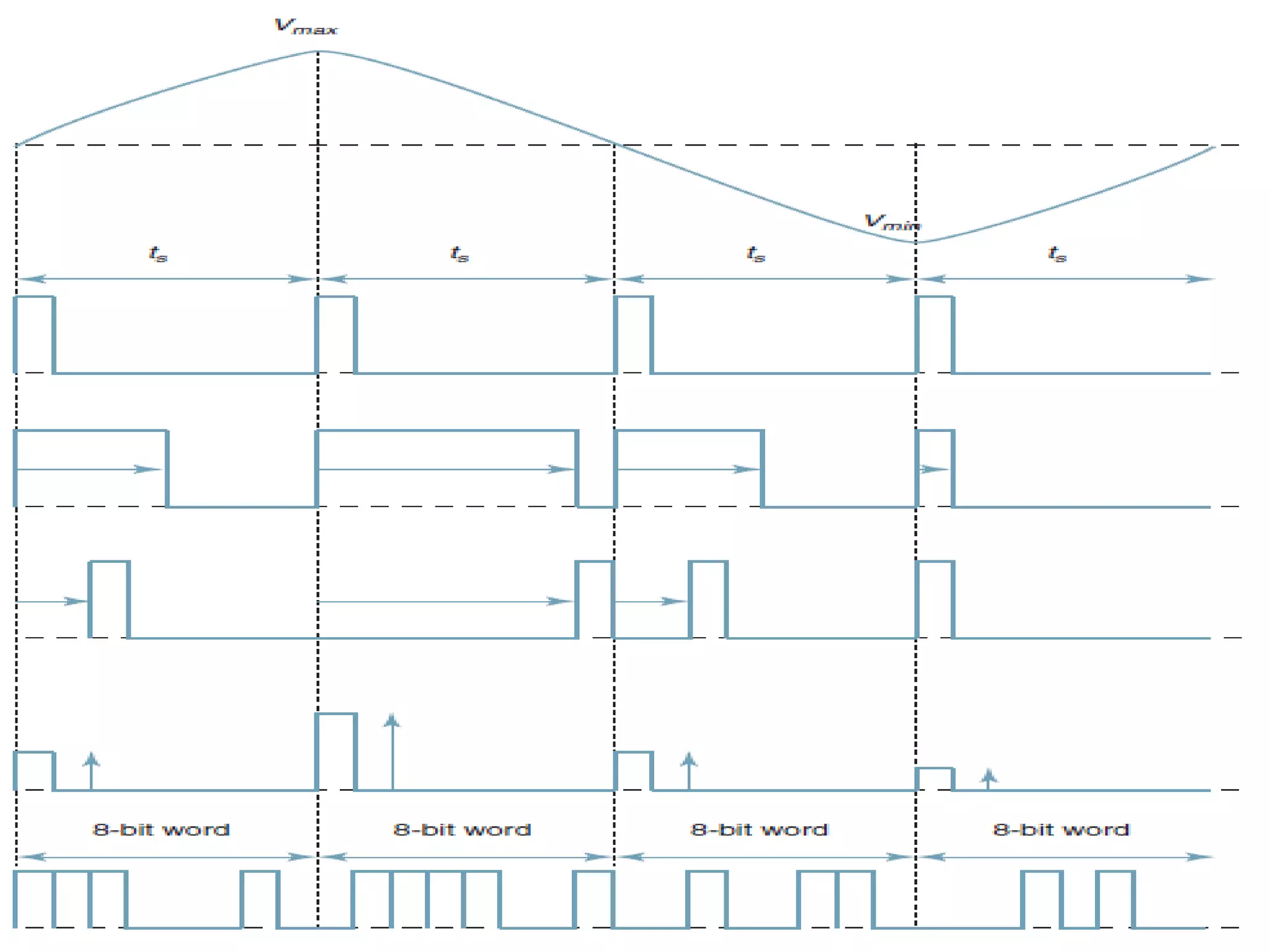
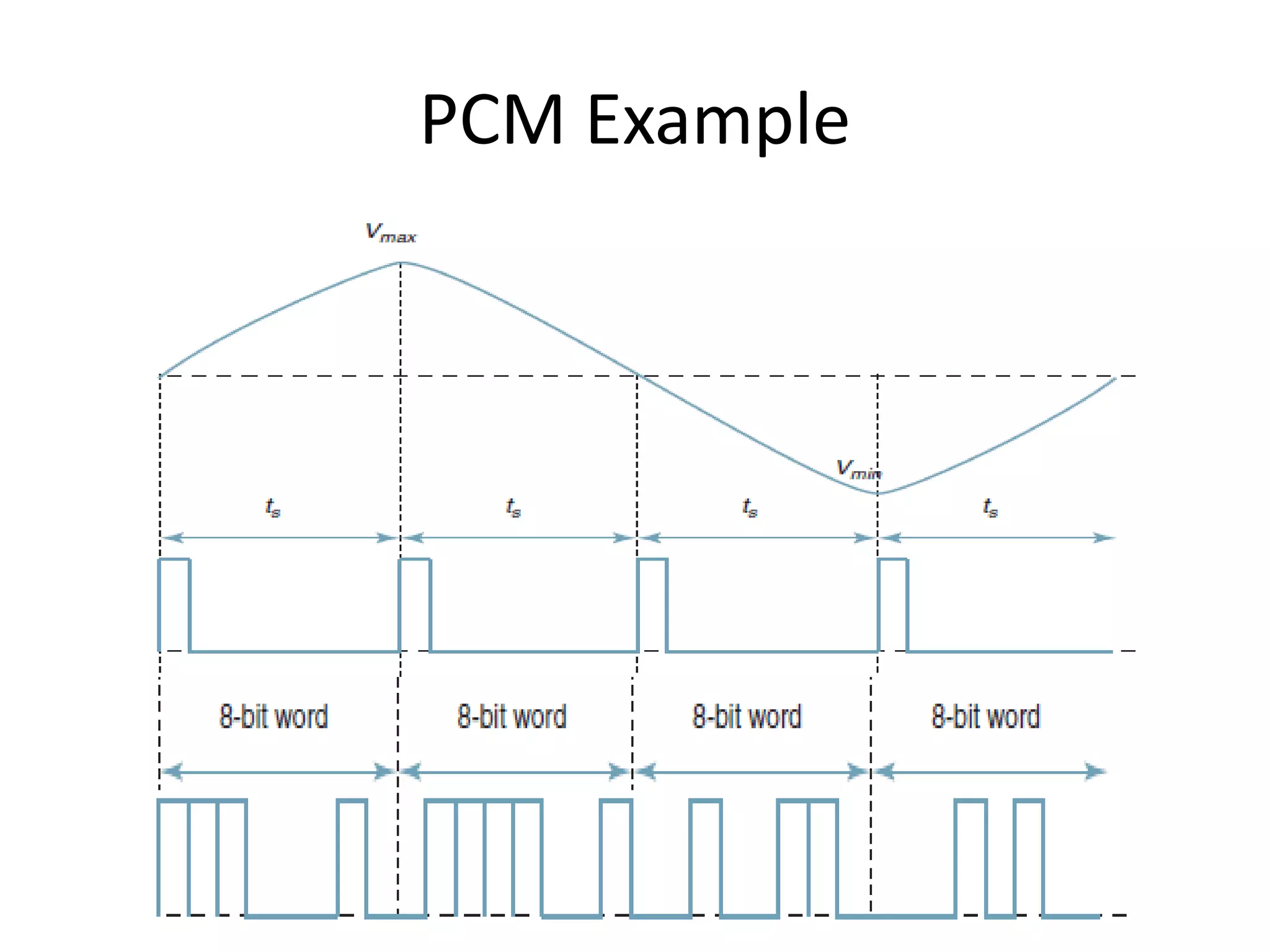
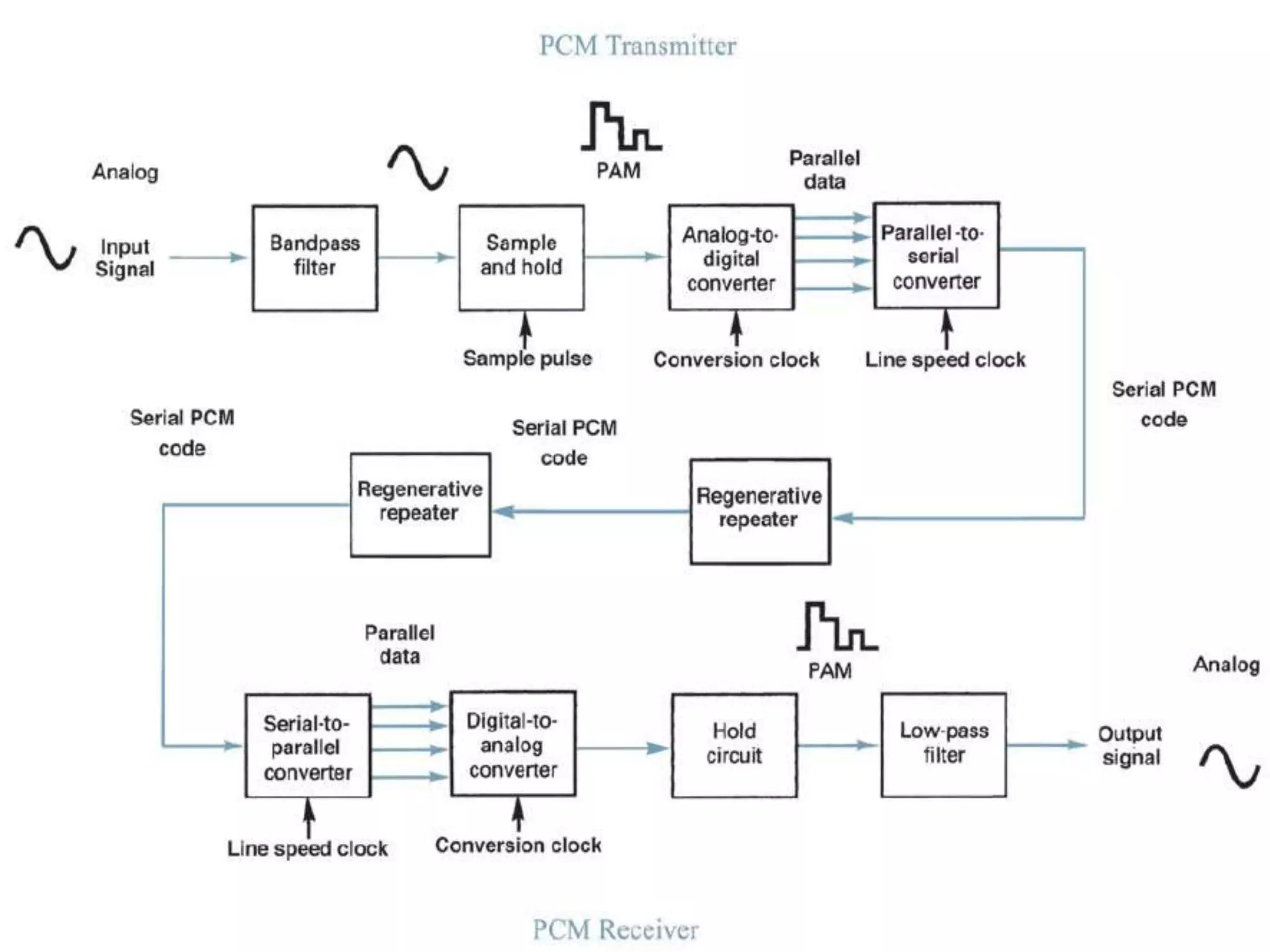
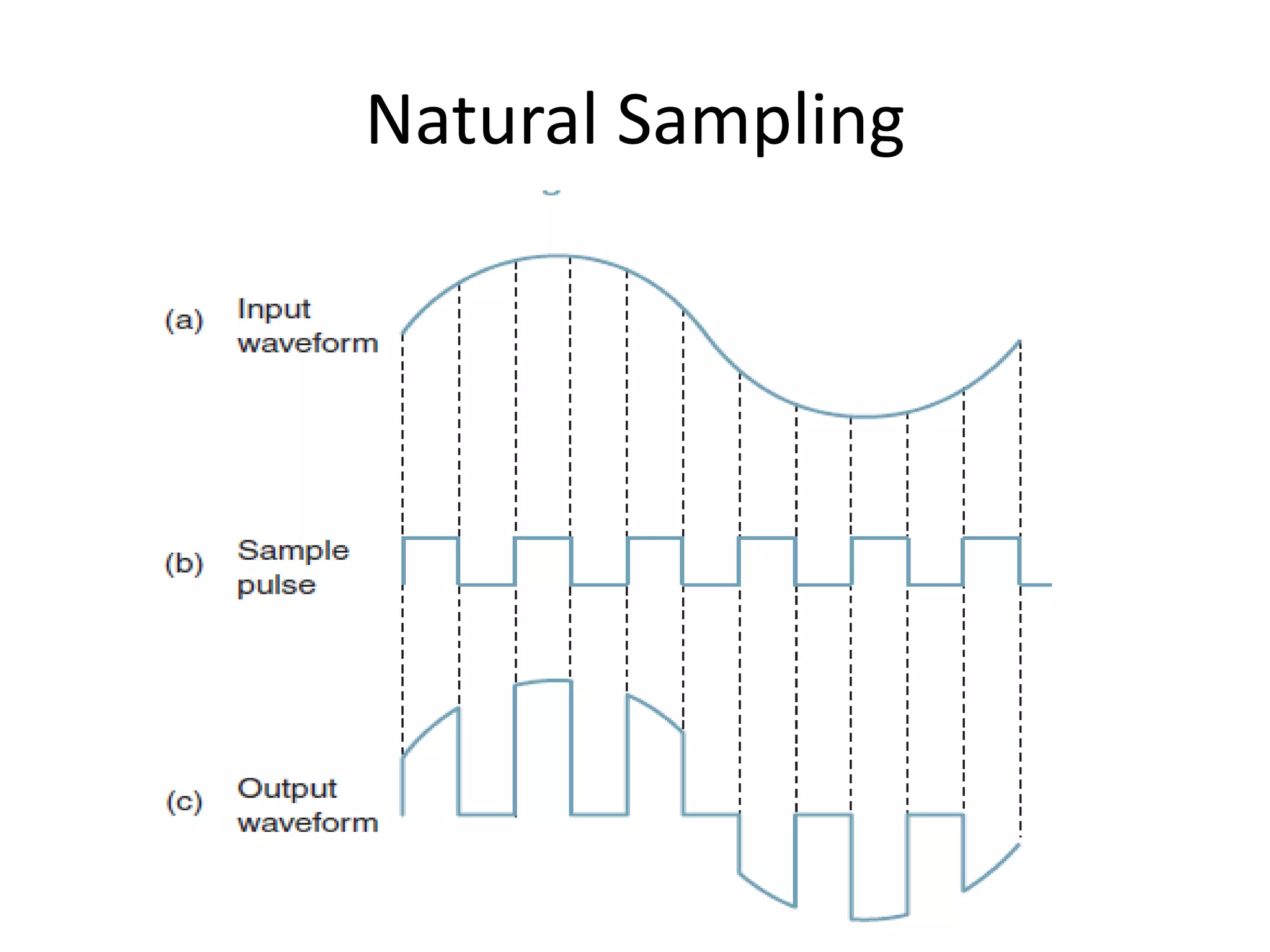
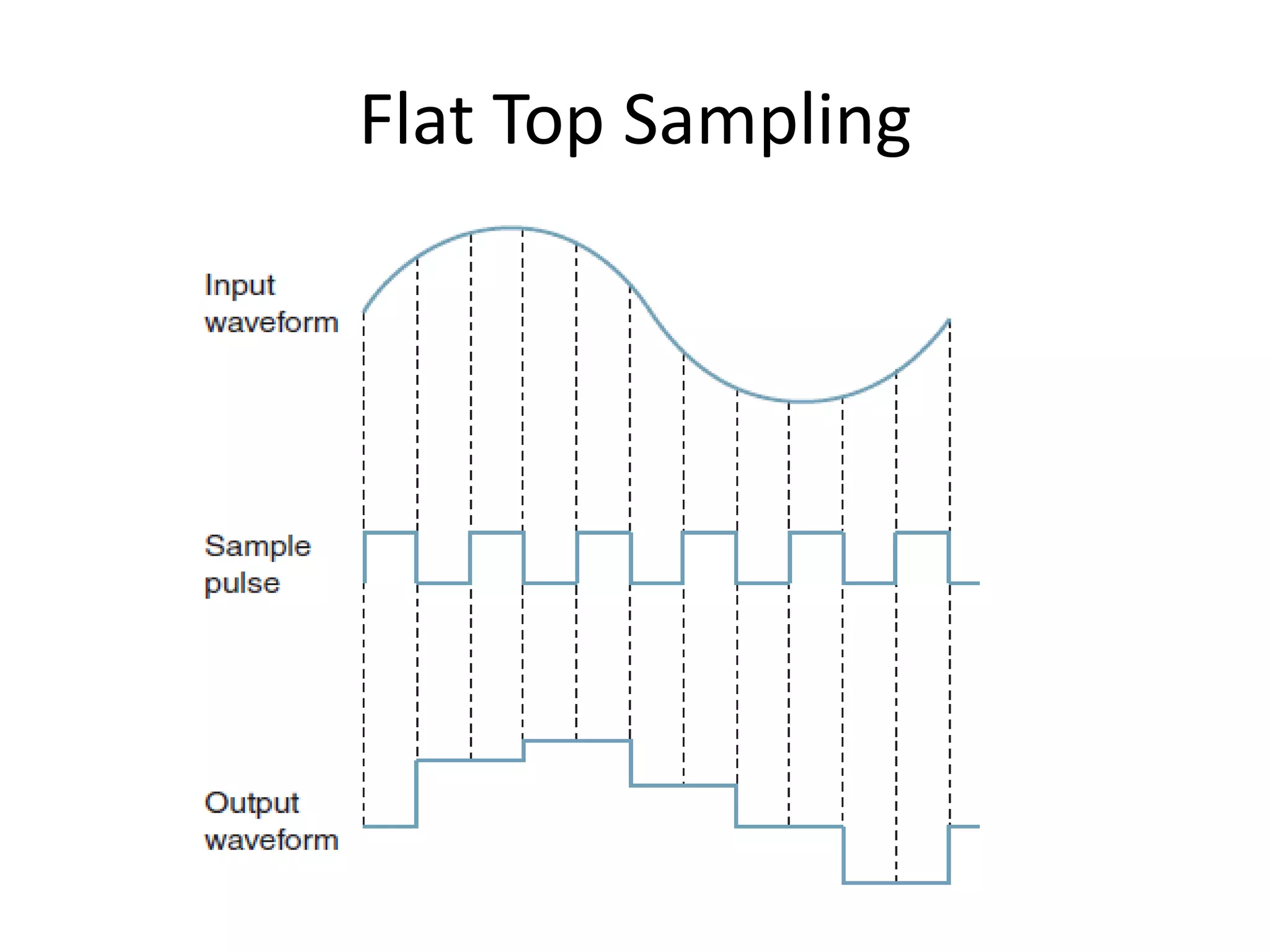
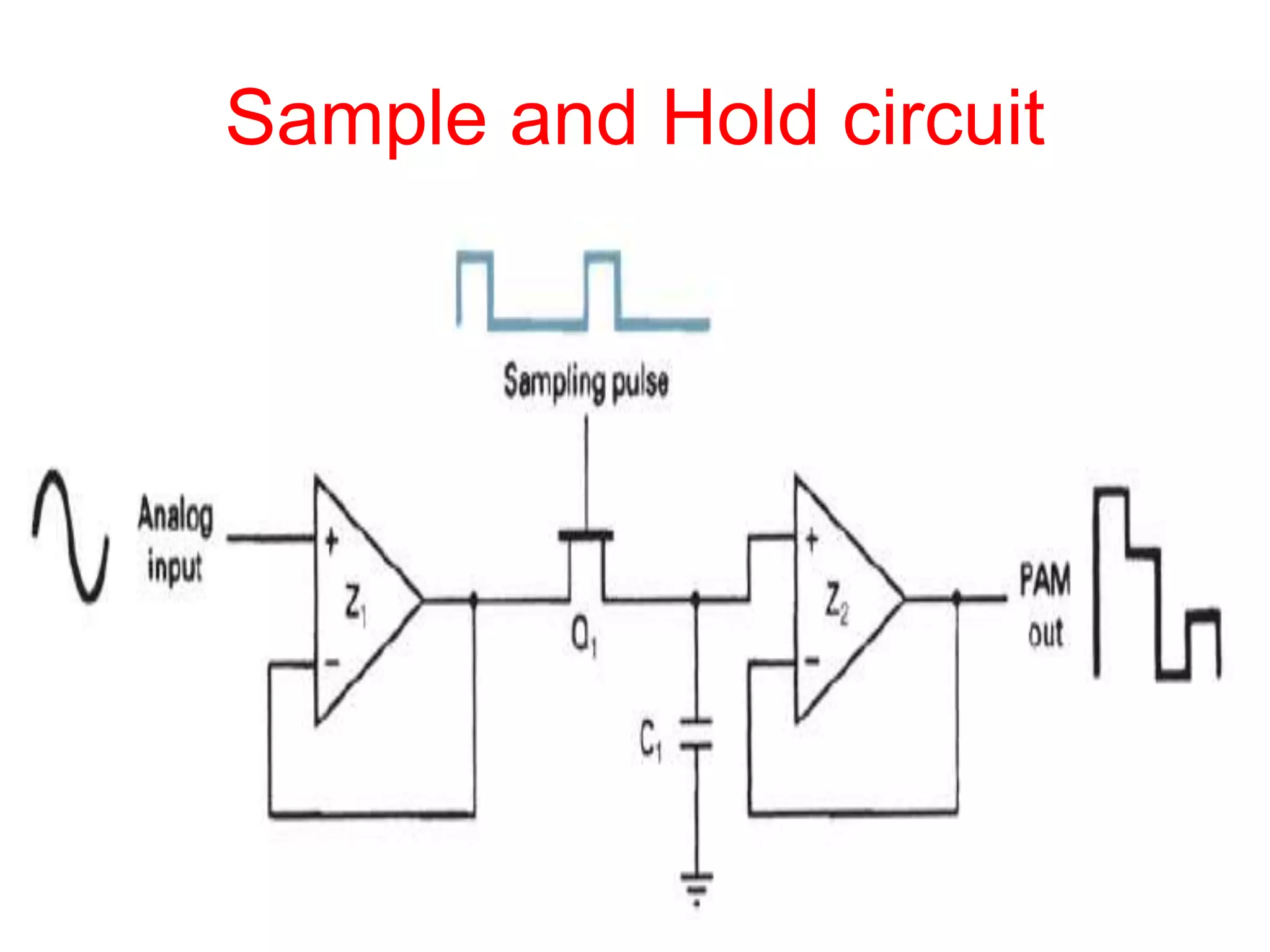
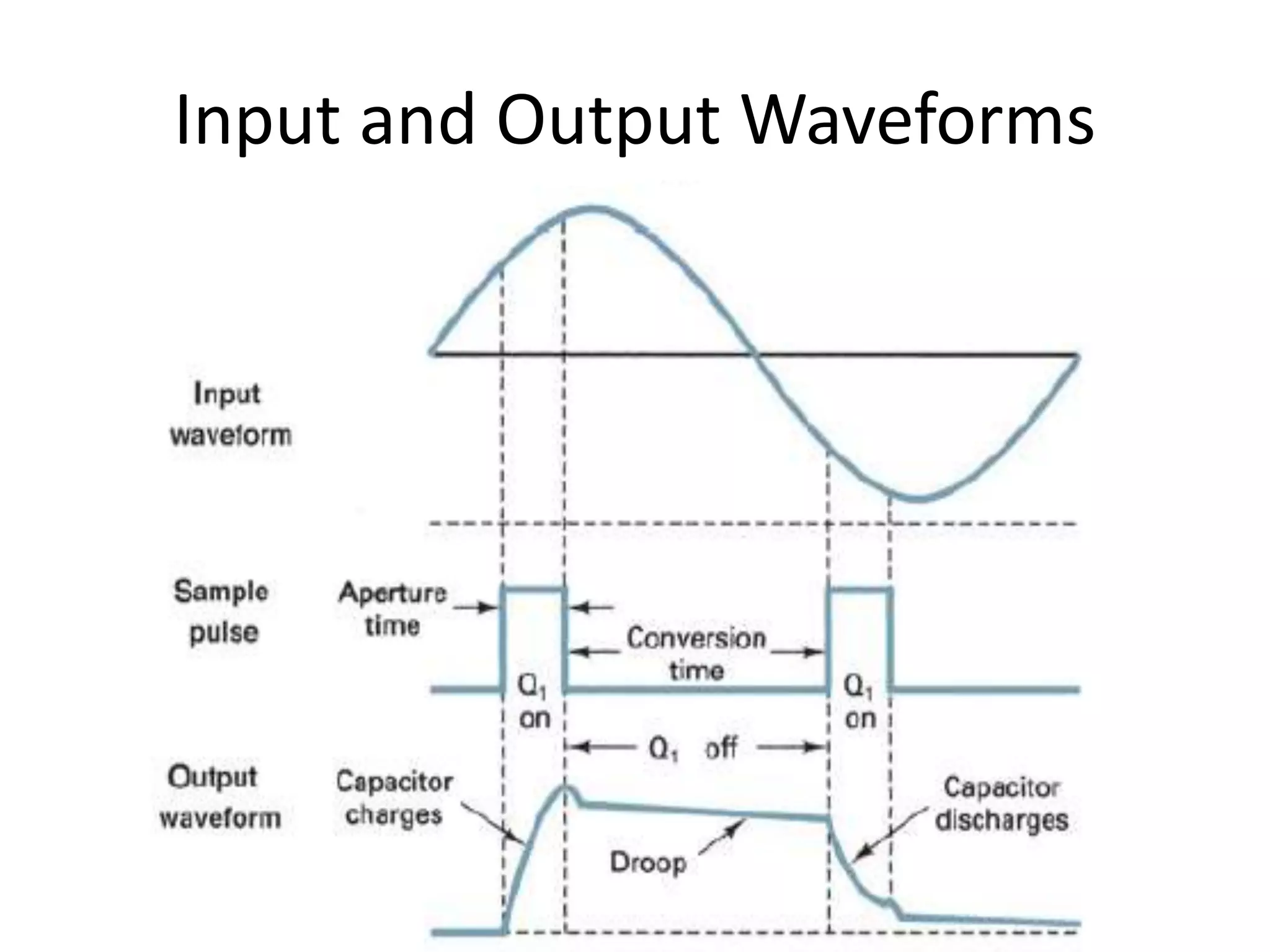
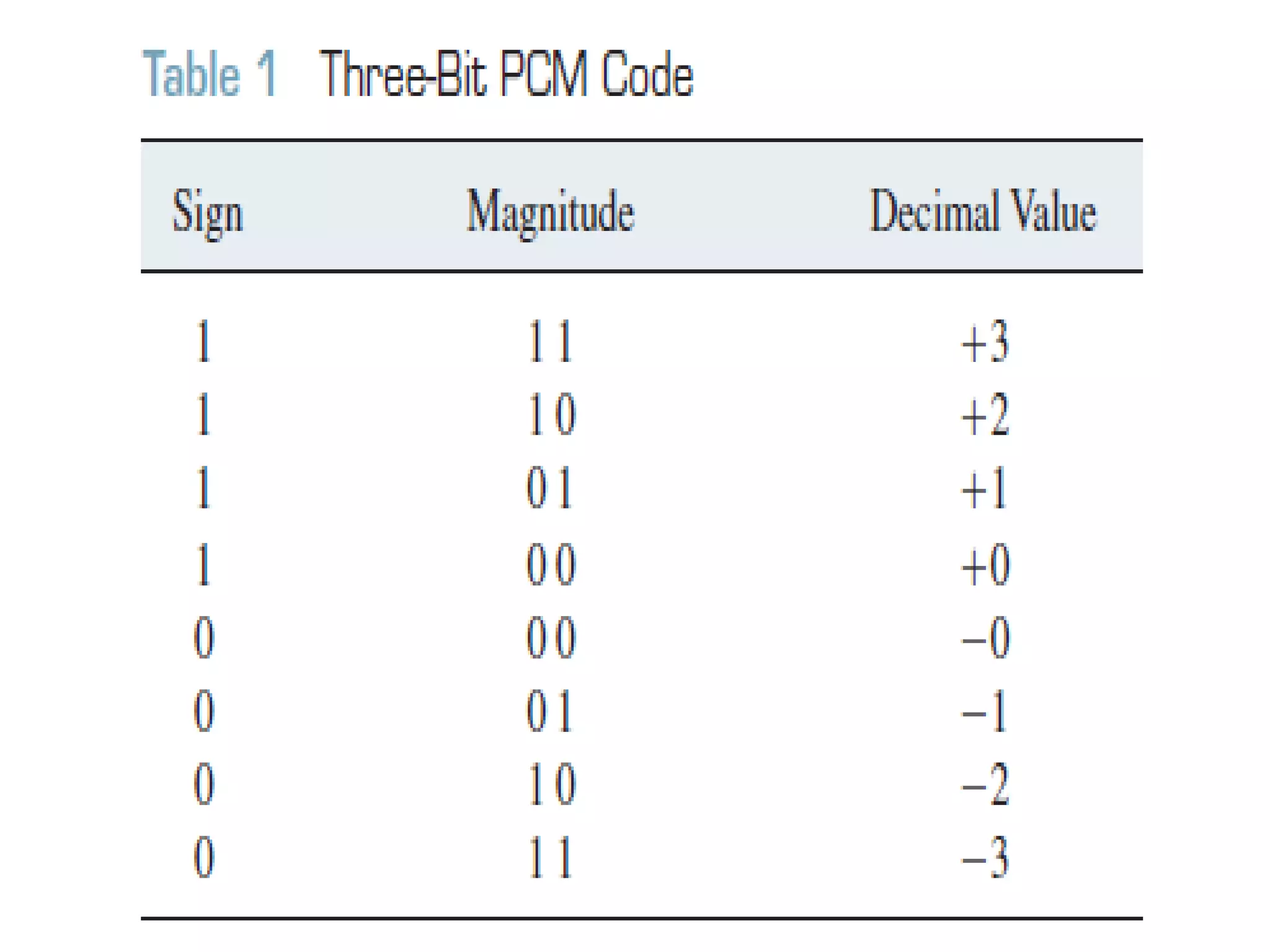
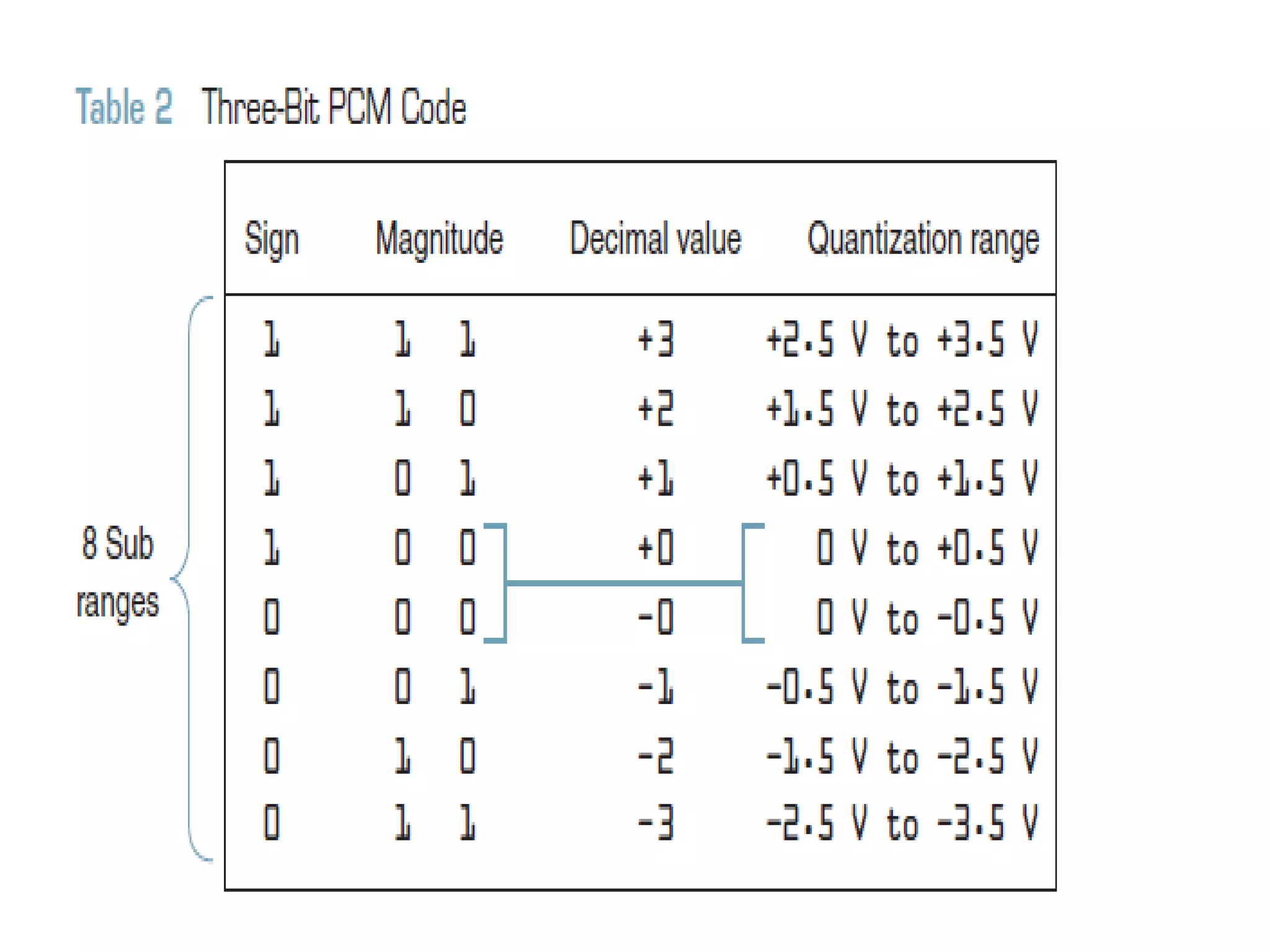
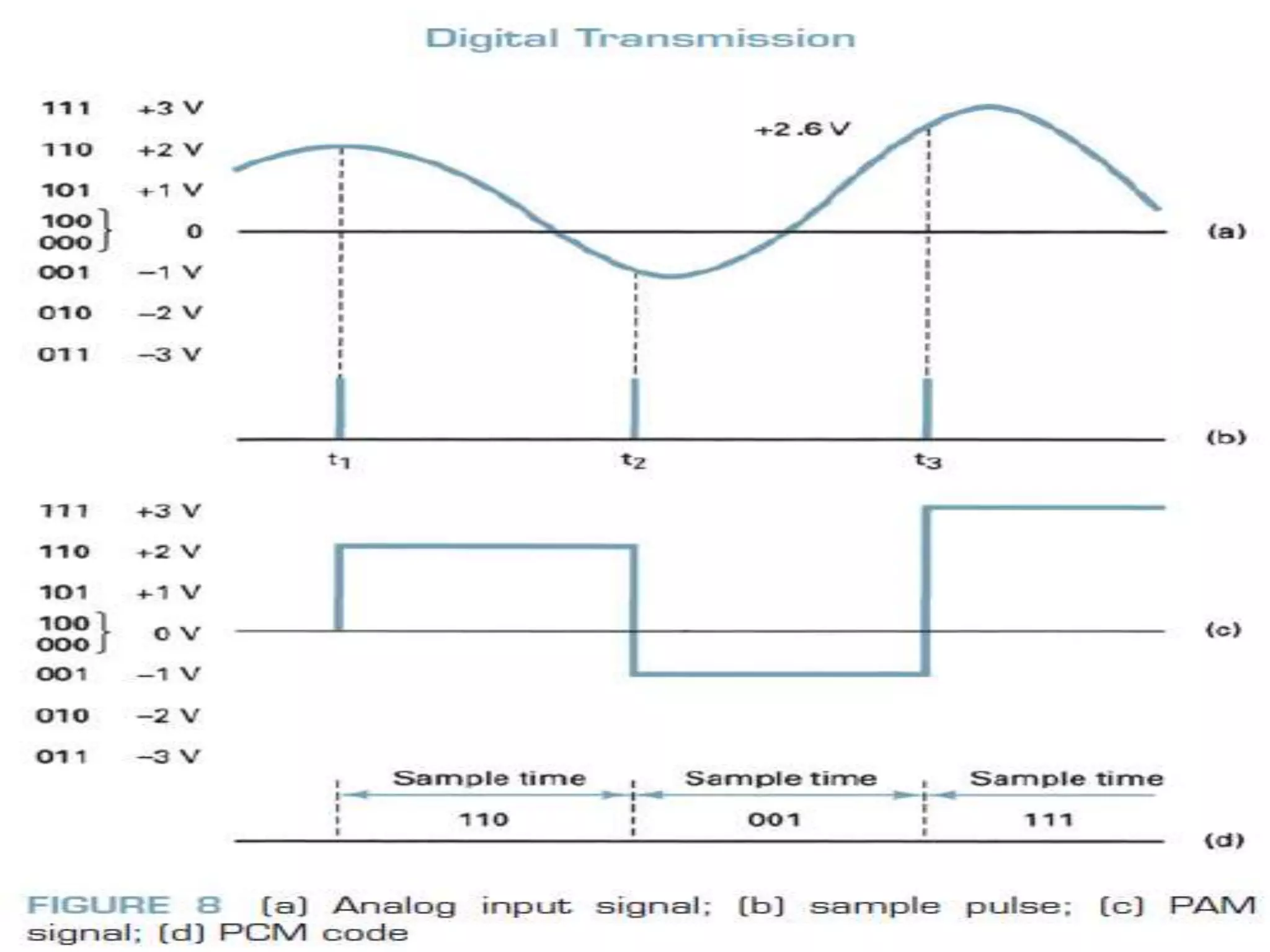
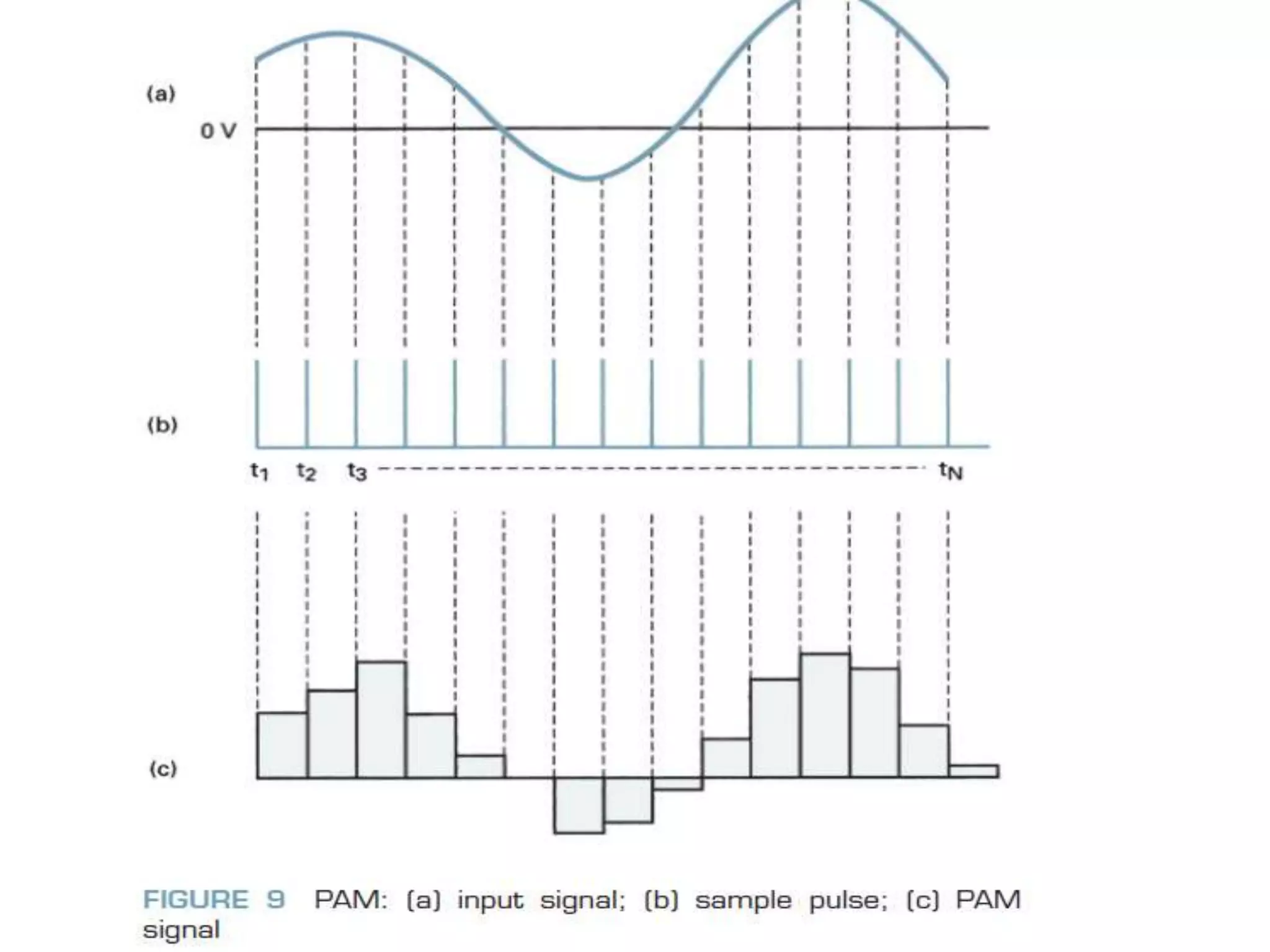
This document provides an overview of digital transmission topics covered in a 10-hour syllabus, with a focus on Pulse Code Modulation (PCM). Key concepts include: PCM involves sampling analog signals and encoding samples into binary codes for transmission; the minimum sampling rate must be at least twice the highest analog frequency to avoid aliasing; and PCM is used widely in telephone networks by encoding voice signals using an analog-to-digital conversion process involving sampling, quantization, coding, transmission and decoding.

1. UNIT II
DIGITAL TRANSMISSION

2. Syllabus (Hours Planned = 10)
• Introduction to Pulse modulation
• Pulse Code Modulation
– PCM sampling
– Sampling Rate
– Quantization and Folded Binary Code
– Dynamic Range
– Signal-to-Quantization Noise Ratio
• Analog companding
• Digital companding
• Delta modulation
• Adaptive Delta Modulation
• Intersymbol interference
• Eye pattens

3. PULSE MODULATION
• Pulse modulation essentially involves
– Sampling analog information signals
– Converting those samples into discrete pulses
• Four predominant methods of pulse modulation
– Pulse Amplitude Modulation (PAM)
– Pulse Width Modulation (PWM)
– Pulse Position Modulation (PPM)
– Pulse Code Modulation (PCM)

5. Pulse Code Modulation (PCM)
• Most prevalent form of pulse modulation
• Used for commercial digital transmission systems.
• In PCM, the analog signal is sampled and then converted to a
serial n-bit binary code for transmission.
• Each code has the same number of bits and requires the
same length of time for transmission.
• The binary codes used for PCM are n-bit codes, where n may
be any positive integer greater than 1.
• In PCM, the pulses are of fixed length and fixed amplitude.

6. Pulse Code Modulation (PCM)
• PCM is the preferred method of communications within the Public
Switched Telephone Network (PSTN)
• PCM is a binary system where a pulse or lack of a pulse within a
prescribed time slot represents either a logic 1 or a logic 0
condition.
• With PCM, it is easy to combine digitized voice and digital data into
a single, high-speed digital signal and propagate it over either
metallic or optical fiber cables.

7. PCM Example

8. Single Channel Simplex PCM
Transmission System

10. Pulse Code Modulation (PCM)
• Bandpass Filter limits the frequency of the analog input signal
to the standard voice-band frequency range of 300 Hz to 3000
Hz.
• Sample-and-hold circuit periodically samples the analog input
signal and converts those samples to a multilevel PAM signal.
• Analog-to-digital Converter (ADC) converts the PAM samples
to parallel PCM codes, which are converted to serial binary
data in the parallel-to-serial converter and then outputted onto
the transmission line as serial digital pulses.
• Transmission line repeaters are placed at prescribed distances
to regenerate the digital pulses.

11. • Serial-to-parallel converter converts serial pulses received
from the transmission line to parallel PCM codes.
• Digital-to-analog Converter (DAC)
– converts the parallel PCM codes to multilevel PAM signals.
• Hold circuit
– basically a lowpass filter that converts the PAM signals back
to its original analog form.
• Codec (coder/decoder)
– An integrated circuit that performs the PCM encoding and
decoding functions is called a codec (coder/decoder)
Pulse Code Modulation (PCM)

12. PCM SAMPLING

13. • The function of a sampling circuit in a PCM transmitter
– To periodically sample the continually changing analog input
voltage
– Then convert those samples to a series of constant amplitude
pulses that can more easily be converted to binary PCM code.
• Impact of ADC Conversion Time
– For the ADC to accurately convert a voltage to a binary code,
the voltage must be relatively constant so that the ADC can
complete the conversion before the voltage level changes.
– If not, the ADC would be continually attempting to follow the
changes and may never stabilize on any PCM code.

14. Basic Techniques of Sampling
• Two basic techniques used to perform the
sampling function
–Natural Sampling
–Flat-top Sampling

15. Natural sampling
• The tops of the sample pulses retain their natural shape
during the sample interval
– It is difficult for an ADC to convert the sample to a PCM code.
• With natural sampling, the frequency spectrum of the sampled
output is different from that of an ideal sample.
• The amplitude of the frequency components produced from
narrow, finite-width sample pulses decreases for the higher
harmonics in a (sin x)/x manner.
• This alters the information frequency spectrum requiring the use of
frequency equalizers (compensation filters) before recovery by a
low-pass filter.

16. Natural Sampling

17. Flat Top Sampling
• Most common method used for sampling voice
signals in PCM systems is flat top sampling,
which is accomplished in a sample-and-hold
circuit.
• With flat-top sampling, the input voltage is
sampled with a narrow pulse and then held
relatively constant until the next sample is taken.

18. Flat Top Sampling

19. • The sampling process alters the frequency spectrum and
introduces an error called aperture error, which is changes in the
amplitude of the sampled signal during the sample pulse time.
• Aperture error prevents the recovery circuit in the PCM receiver
from exactly reproducing the original analog signal voltage.
• The magnitude of error depends on how much the analog signal
voltage changes while the sample is being taken and the width
(duration) of the sample pulse.
• Flat-top sampling introduces less aperture distortion than natural
sampling and can operate with a slower analog-to-digital
converter.

20. Sample and Hold circuit

21. Sample and Hold circuit

22. Input and Output Waveforms

23. • FET acts as a simple analog switch.
• The time that transistor Q1 is on is called the
aperture or acquisition time
• When turned on, Q1 provides a low-impedance path
to deposit the analog sample voltage across
capacitor C1.
• Capacitor C1 is the hold circuit. When Q1 is off, C1
does not have a complete path to discharge through
and, therefore, stores the sampled voltage.

24. • If the input to the ADC is changing while it is performing
the conversion, aperture distortion results.
– By having a short aperture time and keeping the input
to the ADC relatively constant, the sample-and-hold
circuit can reduce aperture distortion.
• Output impedance of voltage follower Z1 and the on
resistance of Q1 must be as small as possible.
• The RC charging time constant of the capacitor is kept
very short, allowing the capacitor to charge or discharge
rapidly during the short acquisition time.

25. • The storage time of the capacitor is called
the A/D conversion time because it is during
this time that the ADC converts the sample
voltage to a PCM code.
• The acquisition time should be very short to
ensure that a minimum change occurs in
the analog signal while it is being deposited
across C1.

26. • Droop: Gradual discharge across the capacitor during
the conversion time.
– caused by the capacitor discharging through its own
leakage resistance and the input impedance of
voltage follower Z2.
• The input impedance of Z2 and the leakage resistance
of C1 be as high as possible.
• Essentially, voltage followers Z1 and Z2 isolate the
sample-and-hold circuit (Q1 and C1) from the input and
output circuitry.

27. Sampling Rate

28. • The Nyquist sampling theorem establishes the
minimum sampling rate (fs) that can be used for a
given PCM system.
• For a sample to be reproduced accurately in a PCM
receiver, each cycle of the analog input signal (fa)
must be sampled atleast twice.
• Consequently, the minimum sampling rate is equal to
twice the highest audio input frequency.
• If fs is less than two times fa, an impairment called
alias or foldover distortion occurs.

29. Nyquist Sampling Theorem
Mathematically, the minimum Nyquist sampling
rate is
fs ≥ 2fa
fs minimum Nyquist sample rate (hertz)
fa maximum analog input frequency
(hertz)

30. • A sample-and-hold circuit is a nonlinear device (mixer) with two inputs: the sampling
pulse and the analog input signal.
– Nonlinear mixing (heterodyning) occurs between these two signals.
– output includes the two original inputs (the audio and the fundamental frequency
of the sampling pulse), their sum and difference frequencies (fs± fa), all the
harmonics of fs and fa (2fs, 2fa, 3fs, 3fa,etc)and their associated cross products
(2fs±fa, 3fs±fa,etc).
• The sampling pulse is a repetitive waveform, it is made up of a series of harmonically
related sine waves.
• Each of these sine waves is amplitude modulated by the analog signal and produces
sum and difference frequencies symmetrical around each of the harmonics of fs.
• Each sum and difference frequency generated is separated from its respective center
frequency by fa.

31. Frequency-domain representation
of the output spectrum

32. • As long as fs is at least twice fa, none of the side frequencies from one
harmonic will spill into the sidebands of another harmonic, and aliasing does
not occur.
• The side frequencies from one harmonic fold over into the sideband of another
harmonic.
• The frequency that folds over is an alias of the input signal (hence the names
“aliasing” or “fold over distortion”).
• If an alias side frequency from the first harmonic folds over into the audio
spectrum, it cannot be removed through filtering or any other technique.
• The input bandpass filter shown in block diagram of PCM is called an
antialiasing or antifoldover filter.
• Its upper cutoff frequency is chosen such that no frequency greater than one-
half the sampling rate is allowed to enter the sample-and-hold circuit, thus
eliminating the possibility of foldover distortion.
Sampling Rate

33. PCM Codes

35. • The codes currently used for PCM are sign-magnitude
codes,
– The most significant bit (MSB) is the sign bit
– Remaining bits are used for magnitude representation.
• The most significant bit is used to represent the sign of
the sample (logic 1 positive and logic 0 negative).
• The two remaining bits represent the magnitude.
– With two magnitude bits, there are four codes possible for positive
numbers and four codes possible for negative numbers.
• Consequently, there is a total of eight possible codes.

36. Quantization and the Folded
Binary Code

37. • Analog signals contain an infinite number of amplitude
possibilities.
• Quantization is the process of converting an infinite
number of possibilities to a finite number of conditions.
• Thus, converting an analog signal to a PCM code with
a limited number of combinations requires
quantization.
• In essence, quantization is the process of rounding off
the amplitudes of flat-top samples to a manageable
number of levels.

38. Quantization Example
• For example, a sine wave with a peak amplitude of
5 V varies between +5 V and -5 V passing through
every possible amplitude in between.
• A PCM code could have only eight bits, which
equates to only 28, or 256 combinations.
• Obviously, to convert samples of a sine wave to
PCM requires some rounding off.

40. • The leftmost bit is the sign bit (1 = + and 0 = -), and the two
rightmost bits represent magnitude.
• This type of code is called a folded binary code because the codes
on the bottom half of the table are a mirror image of the codes on
the top half, except for the sign bit.
• If the negative codes were folded over on top of the positive codes,
they would match perfectly.
• With a folded binary code, each voltage level has one code
assigned to it except zero volts, which has two codes, 100 (0) and
000 (0).
• The magnitude difference between adjacent steps is called the
quantization interval or quantum.

41. • The quantization interval is 1 V.
• For this code, the maximum signal magnitude that can be
encoded is +3 V (111) or -3 V (011), and the minimum signal
magnitude is +1 V (101) or -1 V(001).
• If the magnitude of the sample exceeds the highest
quantization interval, overload distortion (also called peak
limiting) occurs.
• Assigning PCM codes to absolute magnitudes is called
quantizing.

42. Resolution
• Resolution - The magnitude of a quantum
• Resolution is equal to the voltage of the
minimum step size, which is equal to the
voltage of the least significant bit (Vlsb) of the
PCM code.
• The resolution is the minimum voltage other than
0 V that can be decoded by the digital-to-analog
converter in the receiver.
• The smaller the magnitude of a quantum, the
better (smaller) the resolution and the more
accurately the quantized signal will resemble the
original analog sample.

43. • With reference to previous table, each three-bit code has a
range of input voltages that will be converted to that code.
• For example, any voltage between +0.5 and +1.5 will be
converted to the code 101 (+1 V).
• Each code has a quantization range equal to + or - one-half
the magnitude of a quantum except the codes for +0 and -0.
• The 0-V codes each have an input range equal to only one-half
a quantum (0.5 V).

44. Quantization Error
• The likelihood of a sample voltage being equal to one of the eight quantization
levels is remote.
• Each sample voltage is rounded off (quantized) to the closest available
level and then converted to its corresponding PCM code.
• The PAM signal in the transmitter is essentially the same PAM signal produced
in the receiver.
• Any round-off errors in the transmitted signal are reproduced when the code is
converted back to analog in the receiver. This error is called the
QUANTIZATION ERROR (QE).
• The quantization error is equivalent to additive white noise as it alters the
signal amplitude.

46. • Consequently, quantization error is also called quantization noise
(Qn).
• The maximum magnitude for the quantization error is equal to one
half a quantum (0.5 V for the code shown in previous Table).
• The first sample occurs at time t1, when the input voltage is exactly 2
V.
• The PCM code that corresponds to +2 V is 110, and there is no
quantization error.
• Sample 2 occurs at time t2, when the input voltage is -1 V. The
corresponding PCM code is 001, and again there is no quantization
error.
Quantization Error

47. How to determine the PCM code?
• Simply divide the Analog sample voltage by the resolution
• Convert the quotient to an n-bit binary code
• Add the sign bit
• E.g. For sample 3 in previous Figure, the voltage at t3 is
approximately +2.6 V.
• The folded PCM code is
Sample voltage =2.6 / 1 = 2.6
Resolution
• There is no PCM code for 2.6; therefore, the magnitude of the
sample is rounded off to the nearest valid code, which is 111,
or +3 V.

49. • The rounding-off process results in a quantization error of 0.4 V.
• The quantized signal at best only roughly resembles the original
analog input signal.
– Because with a three-bit PCM code, the resolution is rather
poor and also because there are only three samples taken of
the analog signal.
• The quality of the PAM signal can be improved by using a PCM
code with more bits, reducing the magnitude of a quantum and
improving the resolution.
• The quality can also be improved by sampling the analog signal
at a faster rate.