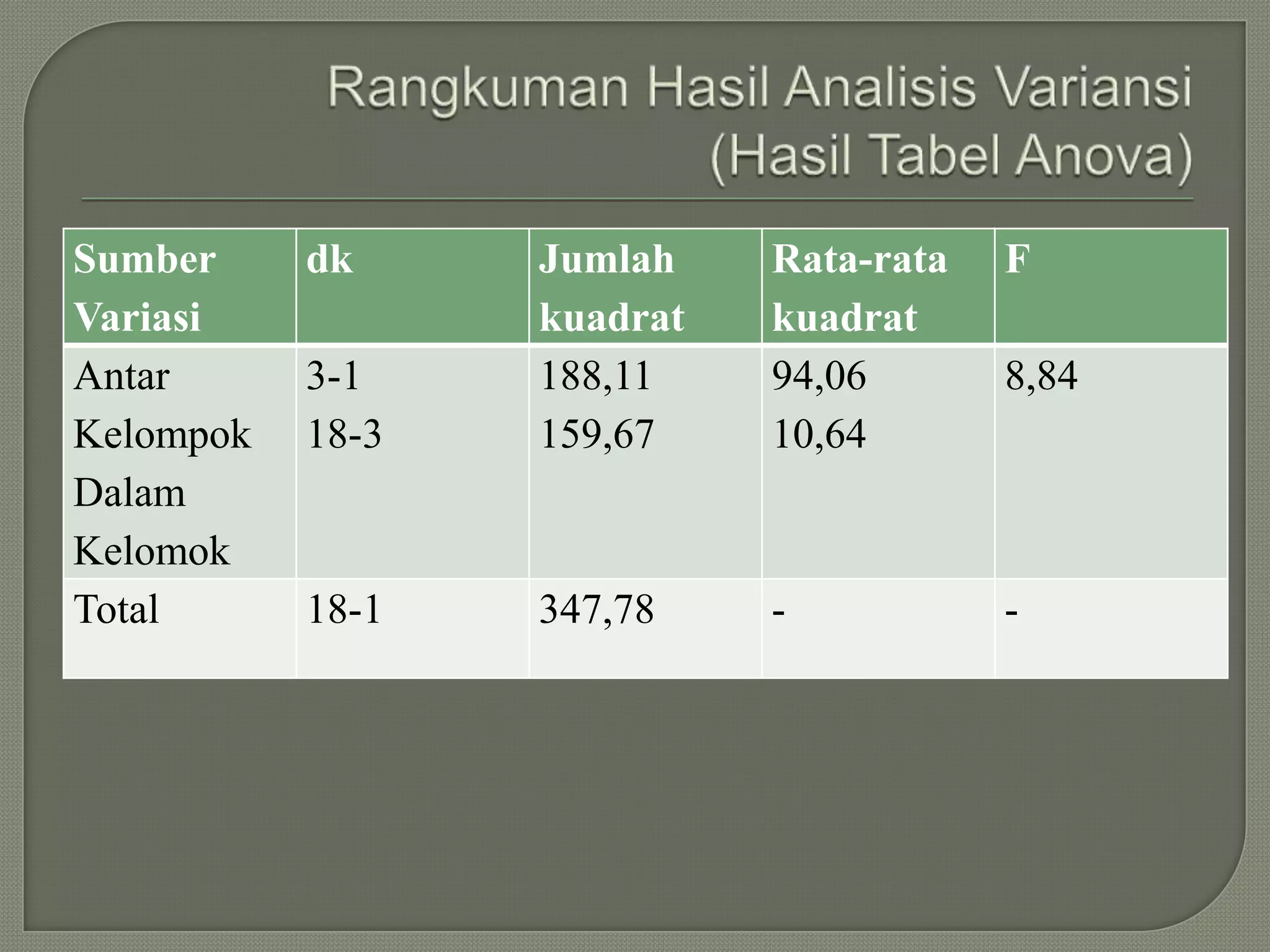
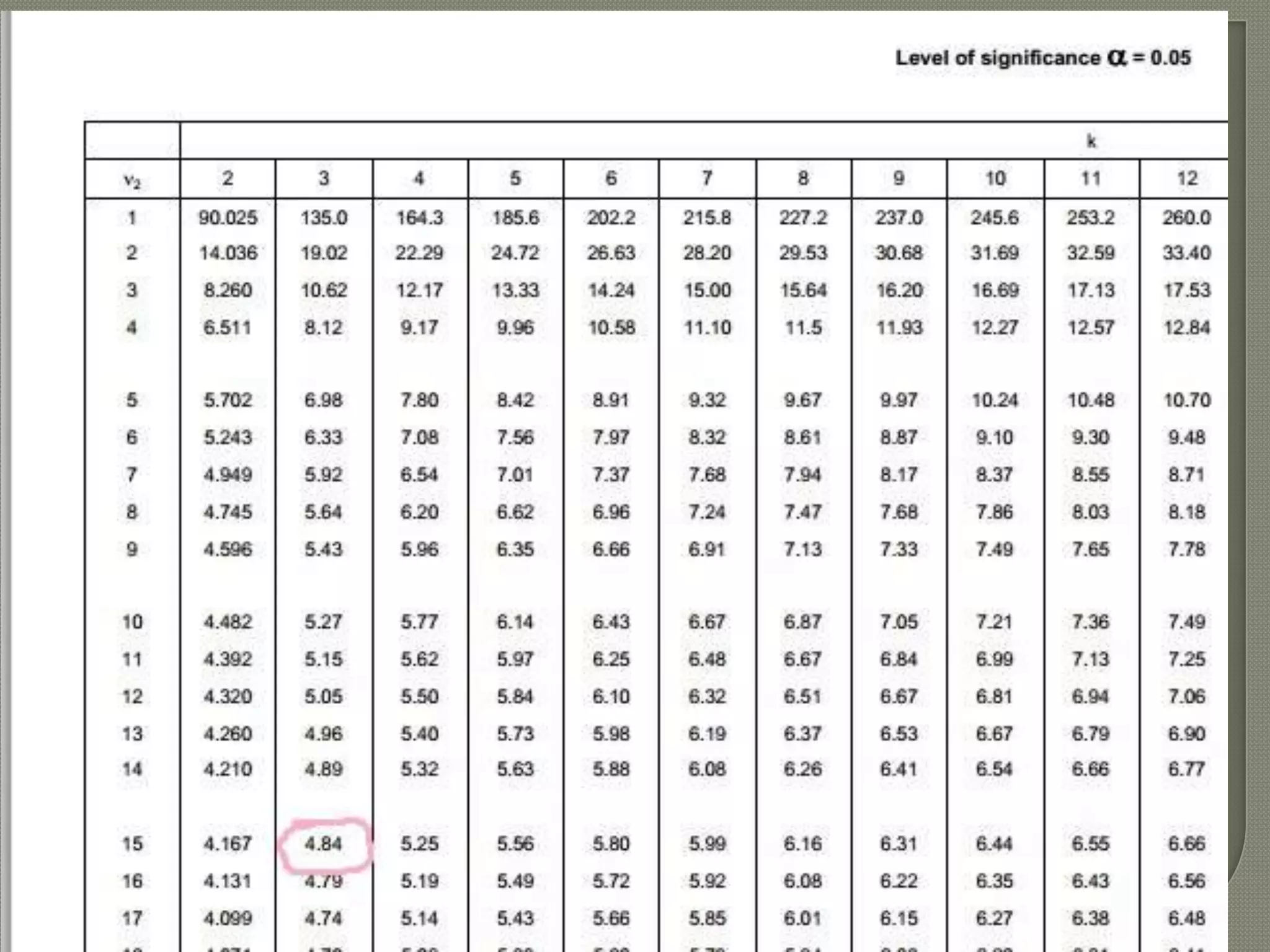
Dokumen ini membahas analisis ANOVA dan metode lanjutan seperti uji Scheffe dan Tukey untuk menentukan perbedaan antara rata-rata populasi. Hasil analisis menunjukkan bahwa hanya kelompok tertentu yang memiliki perbedaan signifikan, sementara uji Tukey menunjukkan dua kontras yang signifikan. Metode ini berguna dalam menguji perbandingan antar kelompok dengan pendekatan yang sederhana dan efektif.

1. Oleh:
Adriana Dwi Ismita 06111008032
Anggun Primadona 06111008005
Dewi Rawani 06111008019
Dwi Kurnia Liztari 06111008034
Nadiah 06111008011
Siti Marfuah 06111008039
Varizka Amelia 06111008033

2.  Penolakan Ho dalam perbandingan sejumlah rata-
rata (dalam anova)= paling sedikit ada dua buah
rata-rata populasi yang berbeda satu sama lain
(simple effect)
 kelompok mana yang berasal dari populasi yang
berbeda tersebut?(kelompok yang memiliki
pengaruh dominan)
 Kemungkinan yang muncul: Kelompok 1 dan 2
; kelompok 1 dan 3 ; kelompok
2 dan 3 ; atau ketiga-tiganya
(khusus anova satu jalur, 3 jenjang), disesuaikan
dengan berapa jalur anova yang digunakan.

3.  Beberapa teknik yang telah dikembangkan
untuk memecahkan dan menjawab
persoalan tersebut : Uji Scheffe dan Tukey
 Halini merupakan analisis yang dilakukan
setelah diketahui anova (Pasca Anova/ uji
lanjut/post hoc test)

4.  Nilai
F atau t hitung dalam anova telah
diketahui

5. Kegunaan:
 menguji perbedaan dua buah rata-rata secara
berpasangan (1 vs 2, 1 vs 3, dan 2 vs 3) dan
perbedaan antara kombinasi rata-rata yang
kompleks (seperti [1+2]/2 vs 3) (Furqon,
2009:213)
 cocokuntuk membuat sembarang
perbandingan yang melibatkan sekelompok
mean. Perhitungan untuk tes scheffe adalah
sangat sederhana dan ukuran sampel tidak
harus sama. (Darmadi, 2011: 292)

6. Langkah pengerjaan dan rumus
 Tentukanhipotesis (disesuaikan dengan
banyak jalur dan jenjang anova)
 Tentukan kriteria pengujian
 Uji
statistik
a. Tentukan kontras antar kelompok ( C )=
perbedaan antara rata-rata yang
dibandingkan
b. Tentukan rumus uji Scheffe
MSw= rata-rata jumlah kuadrat dalam kelompok
n= banyak data
C= kontras antar kelompok

7. c. Tentukan nilai kritis bagi uji Scheffe
k = jumlah kelompok
= nilai pada distribusi
d. Bandingkan antara nilai uji scheffe dan
nilai kritis bagi uji scheffe
 Kesimpulan

8. Model1 Model 2 Model 3
34 35 28
26 30 22
33 37 24
35 28 29
34 31 27
33 30 22
Rata-rata= 32,50 31,83 25,33
Variansi=10,70 11,77 9,47

9. Sumber dk Jumlah Rata-rata F
Variasi kuadrat kuadrat
Antar 3-1 188,11 94,06 8,84
Kelompok 18-3 159,67 10,64
Dalam
Kelomok
Total 18-1 347,78 - -

10.  kontrasuntuk setiap pasangan adalah
Penyelesaiansebagai berikut:
C1 (1 vs 2) = 32,50 – 31,83 = 0,67
C2 (1 vs 3) = 32,50 – 25,33 = 7,17
C3 (2 vs 3) = 31,83 – 25,33 = 6,50
 rumus uji Scheffe masing- masing
kelompok
t1 =0,67/ [2(10,64)/6] = 0,36
t2 = 7,17/[2(10,64)/6] = 3,81
t3 = 6,50/[2(10,64)/6] = 3,45

11.  Jika perbedaan rata-rata setiap pasangan
itu hendak diuji pada tingkat keyakinan
99%( ), maka nilai F kritis
dengan derajat kebebasan 2 (pembilang)
dan 15 (penyebut) adalah 6,36. Atas dasar
itu, kita dapat menentukan nilai kritis ts
sebagai berikut:
ts = (3-1) 6,36
ts = 3,57

12.  Kesimpulan
Dari hasil perhitungan diatas ternyata hanya ada
satu pasangan yang rata-ratanya berbeda signifikan,
yaitu pasangan kelompok 1 dengan kelompok 3. Nilai t
untuk pasangan tersebut adalah 3,81 yang lebih besar
dari nilai kritis uji scheffe (ts = 3,57). Oleh karena itu,
hipotesis nol bahwa rata-rata kedua populasi tersebut
adalah sama harus ditolak. Nilai t untuk kedua pasangan
lainnya ternyata lebih kecil daripada nilai kritisnya,
sehinggga hipotesis nol yang bersangkutan tidak dapat
ditolak. Secara simbolik , kesimpulan tersebut dapat
ditulis sebagai berikut :

13. Kegunaan:
 hanya dapat digunakan untuk menguji
seluruh kemungkinan pasangan
sederhana, tidak bisa untuk kompleks
(Furqon, 2009: 215).
 lebih powerful (cenderung lebih sering
menolak hipotesis nol) karena jumlah
kemungkinan pasangan yang hendak diuji
relative sedikit (Furqon, 2009: 215).

14.  Tentukanhipotesis (disesuaikan dengan
banyak jalur dan jenjang anova)
 Tentukan kriteria pengujian
 Uji
statistik
a. Tentukan kontras antar kelompok ( C
)= perbedaan antara rata-rata yang
dibandingkan

15. b. Tentukan nilai kritis HSD
q= nilai pada distribusi studentized range
statistic
 Bandingkan nilai HSD dengan nilai kontras (
C)
 Kesimpulan

16. Model1 Model 2 Model 3
34 35 28
26 30 22
33 37 24
35 28 29
34 31 27
33 30 22
Rata-rata= 32,50 31,83 25,33
Variansi=10,70 11,77 9,47

17. Sumber dk Jumlah Rata-rata F
Variasi kuadrat kuadrat
Antar 3-1 188,11 94,06 8,84
Kelompok 18-3 159,67 10,64
Dalam
Kelomok
Total 18-1 347,78 - -

18.  Nilai kontras
 Nilai
kritis HSD
q pada dengan derajat kebebasan
15 dan 3 adalah 4,84.
HSD= 4,84 (10,46/6)
HSD= 6,45

20. .
 Kesimpulan
Hasil tersebut menunjukkan ada dua buah
nilai kontras antara rata- rata setiap
pasangan yang lebih besar daripada nilai
kritis HSD. Dengan kata lain, uji Tukey
menghasilkan dua kontras yang signifikan
pada , yaitu kontras dan
kontras . Contoh ini sekaligus
membuktikan ungkapan di atas bahwa uji
Tukey cenderung lebih sering menolak
hipotesis nol daripada uji Scheffe.