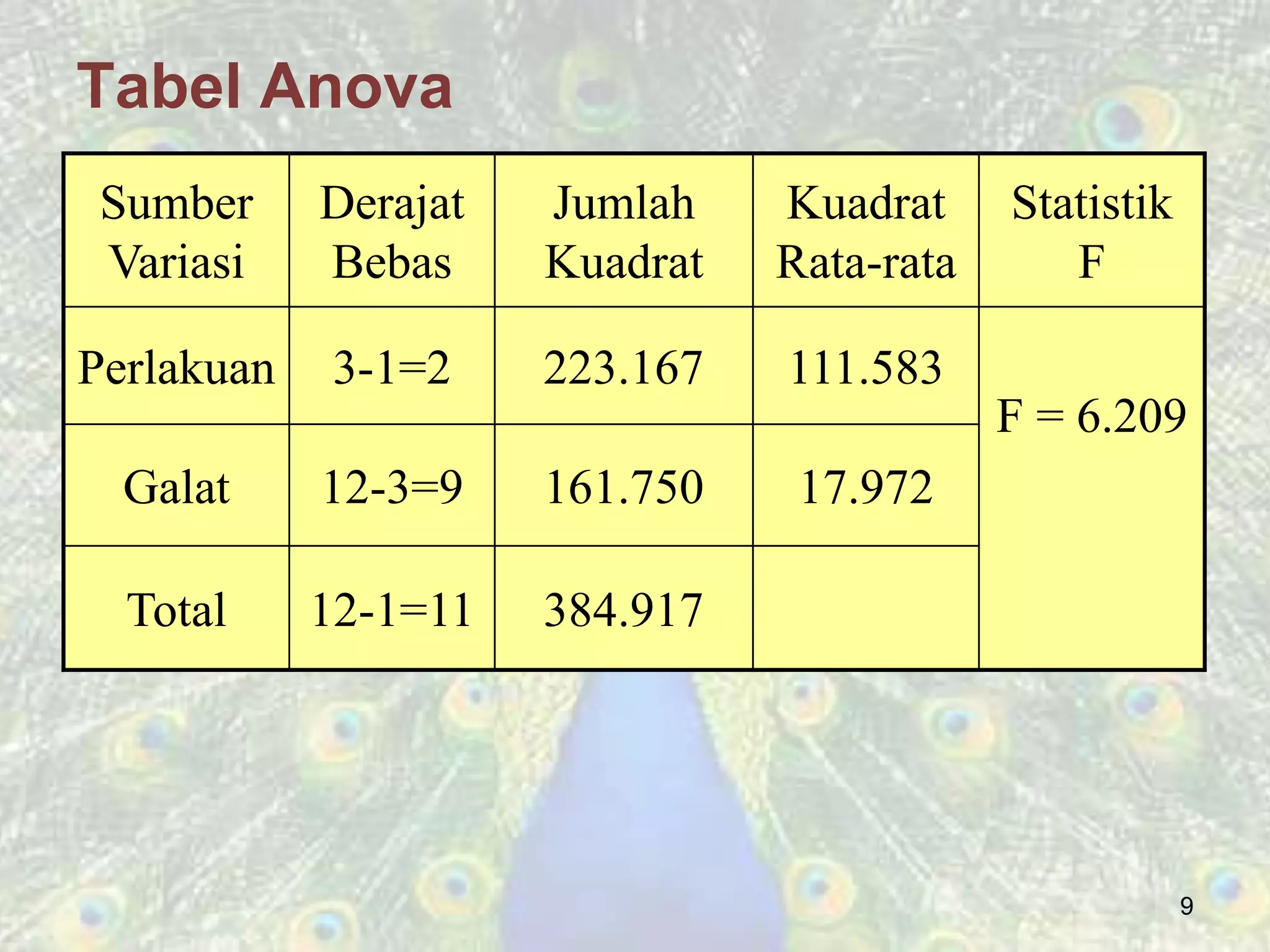
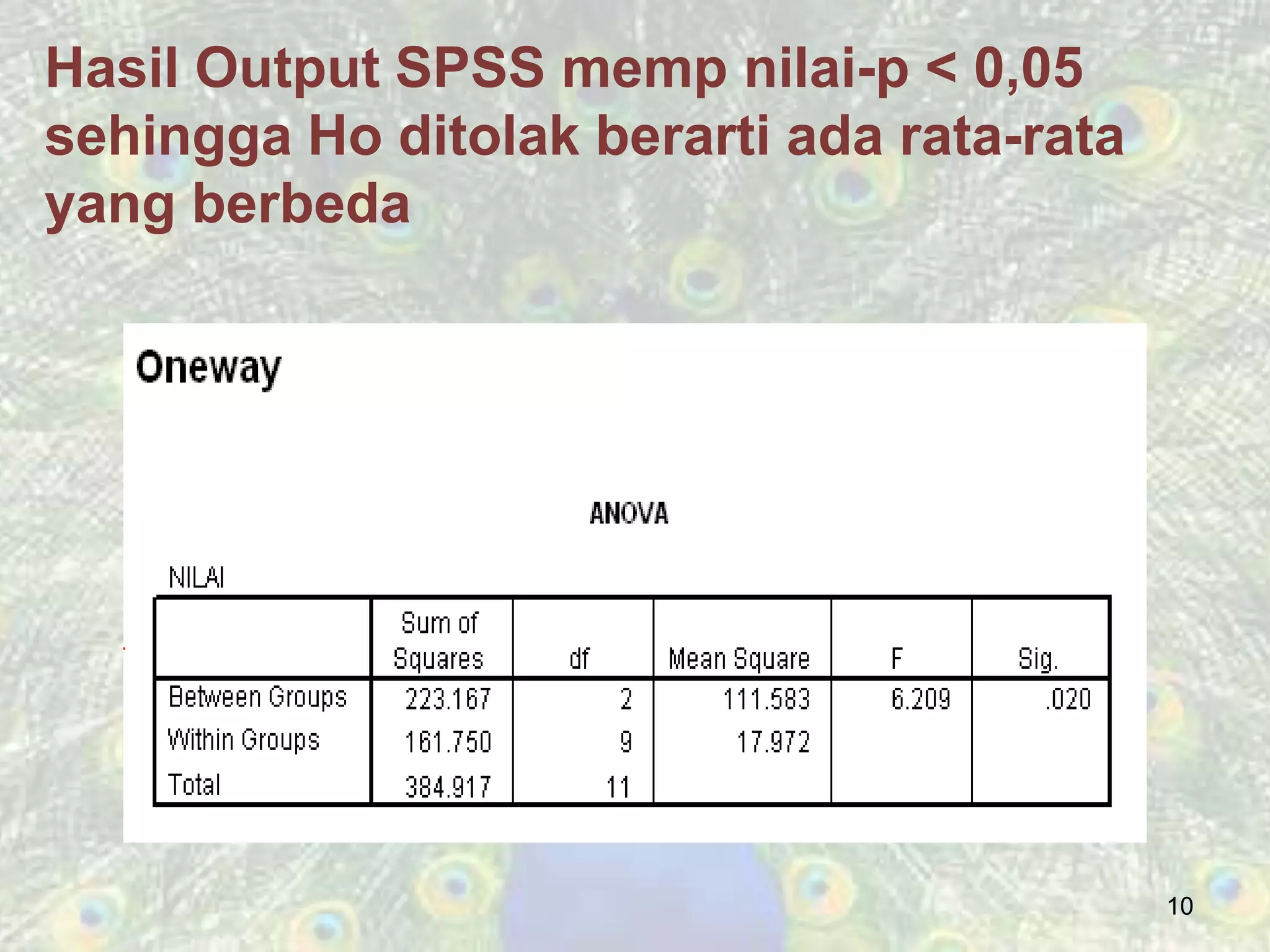
Analisis variansi (ANOVA) digunakan untuk menguji hipotesis kesamaan rata-rata dari tiga populasi atau lebih dengan kondisi bahwa sampel diambil secara acak, berdistribusi normal, dan memiliki variansi yang sama. Dalam contoh, hasil menunjukkan bahwa ada perbedaan signifikan antara metode pengajaran menggunakan nilai p yang lebih kecil dari 0,05. Post hoc tests digunakan untuk mengidentifikasi kelompok mana yang berbeda secara signifikan setelah hipotesis nol ditolak.