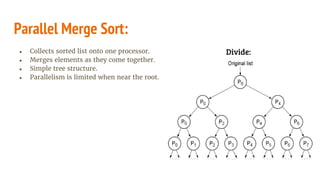
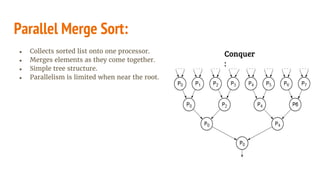
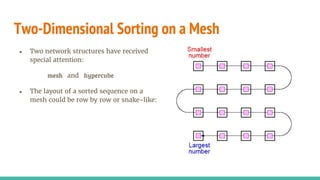
The document discusses various parallel sorting algorithms, including parallel bubble sort, parallel merge sort, bitonic sort, and shear sort, highlighting their goals, complexities, and operational principles. It emphasizes that parallel algorithms can significantly reduce sorting time, with optimal complexities for different algorithms outlined. Additionally, it provides insights into the execution processes, including phase-based operations for algorithms like parallel bubble sort and shear sort, as well as the characteristics and sorting mechanisms of bitonic lists.








![Parallel Bubble Sort:
Algorithm:
1. For k = 0 to n-1
2. If k is even then
3. for i = 0 to (n/2) do in parallel
4. If A[2i] > A[2i+1] then
5. Exchange A[2i] ↔ A[2i+1]
6. Else
7. for i = 0 to (n/2)-1 do in parallel
8. If A[2i+1] > A[2i+2] then
9. Exchange A[2i+1] ↔ A[2i+2]
10. Next k](https://image.slidesharecdn.com/parallelalgosorting-160629122904/85/Parallel-sorting-Algorithms-9-320.jpg)