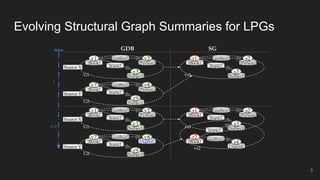
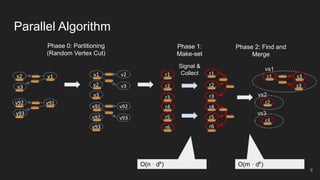
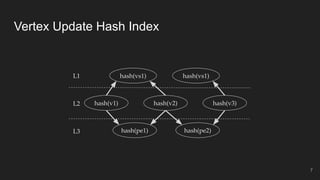
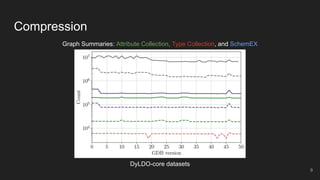
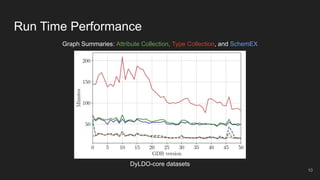
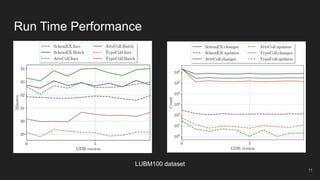
This document presents an incremental and parallel algorithm for computing structural graph summaries of evolving graphs. The algorithm incrementally updates graph summaries when the input graph changes, which is often faster than recomputing from scratch. The algorithm partitions the graph and computes summaries in parallel. Experimental results on real-world and benchmark graphs show the incremental algorithm outperforms batch computation even when 50% of the graph changes. The algorithm runs in linear time with respect to graph changes and degree.

1. Incremental and Parallel Computation of
Structural Graph Summaries
for Evolving Graphs
Till Blume1
, David Richerby2
, and Ansgar Scherp3
CIKM 2020, Virtual Event
1
Kiel University, Germany
2
University of Essex, United Kingdom
3
Ulm University, Germany

2. Structural Graph Summaries
Structural graph summaries are a condensed representation of graphs such that a
set of chosen (structural) features in the graph summary are equivalent to the
original graph.
Structural Features (f1
,..., fx
)
Input Graph
Structural Graph Summary
2

3. G2
G1
G2
G1 vs1
Evolving Structural Graph Summaries for LPGs
SGGDB
{Person}
v2
{Book}
v1
{Subject}
v3
{author}
{topic}Source X
{Person}
v8
{Book}
v7
{Subject}
v9
{author}
{topic}Source Y
{Person}
s2
{Book}
r1
{Subject}
s3
{author}
{topic}
{Person}
v2
{Book}
v1
{Subject}
v3
{author}
{topic}Source X
{Agent}
v8
{Book}
v7
{Subject}
v9
{author}
{topic}
{Person}
s2
{Book}
r1 {author}
{topic}
vs1
time
t
t+1 {Subject}
s3
{Book}
r2
{Agent}
s4
{topic}
{author}
vs2Source Y
3

4. Problem Definition
● there are various different structural features that can be used to summarize
● when the input graph changes, it is often prohibitively expensive to recompute
the structural graph summary from scratch
● existing incremental algorithms are often not designed for evolving graphs or
require an explicit change log
4

5. Contribution
1. generic, parallel algorithm to incrementally compute and update structural
graph summaries and as well as a generic data structure following our formal
language
2. theoretical complexity analysis: all graph summaries defined in the formal
language can be updated in O(∆·dk
), with ∆ changes the input graph, d is the
maximum degree of the input graph, and k is the maximum distance in the
subgraphs considered for the equivalence
3. empirical analyses on benchmark and real-world datasets: our
incremental algorithm outperforms a batch computation even with about 50%
of the graph changed
5

6. Parallel Algorithm
Phase 2: Find and
Merge
Phase 1:
Make-set
v1
v3
Signal &
Collectv2
v91
v93
v92
v1
v3
v2
v3
Phase 0: Partitioning
(Random Vertex Cut)
v2
v91
v93
v92
v93v92
r1
r2
r3
r4
r5
r6
r1
r2
r3
r4
r6
r5
r1 s3
r2
vs1
vs2
r3
vs3
s3
O(n · dk
) O(m · dk
)
6

7. Vertex Update Hash Index
hash(v1)
hash(vs1)
hash(pe1)
hash(v2) hash(v3)
hash(vs1)
hash(pe2)
L1
L2
L3
7

8. Experimental Evaluation
Datasets
● LUBM100 (~2.1 M vertices and ~13 M edges)
● BSBM (up to 1.3 M vertices and 13 M edges)
● DyLDO-core (2.1–3.5 M vertices and 7–13 M edges)
● DyLDO-ext (7–10 M vertices and 84–106 M edges)
Summary Models
● Attribute Collection
● Type Collection
● SchemEX
In total, 312 experiments for incremental and for batch each
8

9. Compression
DyLDO-core datasets
9
Graph Summaries: Attribute Collection, Type Collection, and SchemEX

10. Run Time Performance
Graph Summaries: Attribute Collection, Type Collection, and SchemEX
DyLDO-core datasets
10

11. Run Time Performance
LUBM100 dataset
11

12. Conclusion
1. generic, parallel algorithm to incrementally compute and update structural graph
summaries and as well as a generic data structure following our formal language
2. theoretical complexity analysis: all graph summaries defined in the formal
language can be updated in O(∆·dk
), with ∆ changes the input graph, d is the
maximum degree of the input graph, and k is the maximum distance in the
subgraphs considered for the equivalence
3. empirical analyses on benchmark and real-world datasets: our incremental
algorithm outperforms a batch computation even with about 50% of the graph
changed
Source Code and all resources available on GitHub:
https://github.com/t-blume/fluid-spark 12