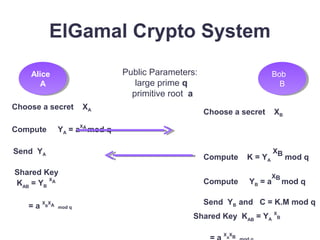
This document discusses several public key cryptosystems based on discrete logarithms, including Diffie-Hellman key exchange, ElGamal encryption, and ElGamal digital signatures. It provides examples of how each system works using mathematical operations like exponentiation modulo a prime number. Diffie-Hellman allows two parties to securely generate a shared secret key over an insecure channel. ElGamal encryption and signatures extend this idea to allow public key encryption and digital signatures based on the difficulty of solving discrete logarithms.

1. Other Public Key Systems

2. Outline
 Primitive Element Theorem
 Diffie Hellman Key Distribution
 ElGamal Encryption
 ElGamal Digital Signatures

3. Discrete Logarithm(s) (DLs)
 Fix a prime p. Let a, b be nonzero integers
(mod p). The problem of finding x such
that ax
≡ b (mod p) is called the discrete
logarithm problem. Suppose that n is the
smallest integer such that an
≡1 (mod p),
i.e., n=ordp(a). By assuming 0≤x<n, we
denote x=La(b), and call it the discrete log
of b w.r.t. a (mod p)
 Ex: p=11, a=2, b=9, then x=L2(9)=6

4. Discrete Logarithms
 In the RSA algorithms, the difficulty of
factoring a large integer yields good
cryptosystems
 In the ElGamal method, the difficulty of
solving the discrete logarithm problem
yields good cryptosystems
 Given p, a, b, solve ax
≡ b (mod p)
 a is suggested to be a primitive root mod p

5. One-Way Function
 A function f(x) is called a one-way function
if f(x) is easy to compute, but, given y, it is
computationally infeasible to find x with
y=f(x).
 La(b) is a one-way function if p is large

6. Primitive Roots mod 13
 The primitive root a is a number whose
powers successively generate all the
elements mod p.

7. Example
 p = 11; a = 2.
 22
= 4, 23
= 8, 24
= 5, 25
= 10, 26
= 9,
27
= 7, 28
= 3, 29
= 6, 210
= 1 (mod 11)
 32
= 9, 33
= 5, 34
= 4, 35
= 1 (mod 11)
 The residue (2 mod 11) can create all
non-zero residues mod 11 via
exponentiation. It is called a generator.
 The residue (3 mod 11) does not have
the same property.

8. 88
Public Key Distribution
 The goal is for two users to securely exchange a key
over an insecure channel. The key is then used in a
normal cryptosystem

9. Diffie-Hellman Key Exchange
 first public-key type scheme proposed
 by Diffie & Hellman in 1976 along with the
exposition of public key concepts

note: now know that Williamson (UK CESG)
secretly proposed the concept in 1970
 is a practical method for public exchange
of a secret key
 used in a number of commercial products

10. Diffie-Hellman Key Exchange
 a public-key distribution scheme

cannot be used to exchange an arbitrary message

rather it can establish a common key

known only to the two participants
 value of key depends on the participants (and
their private and public key information)
 based on exponentiation in a finite (Galois) field
(modulo a prime or a polynomial) - easy
 security relies on the difficulty of computing
discrete logarithms (similar to factoring) – hard

11. Diffie-Hellman Setup
 all users agree on global parameters:

large prime integer or polynomial q

a being a primitive root mod q
 each user (eg. A) generates their key
 chooses a secret key (number): xA < q

compute their public key: yA = a
xA
mod q
 each user makes public that key yA

12. Diffie-Hellman Key Exchange
 shared session key for users A & B is KAB:
KAB = a
xA.xB
mod q
= yA
xB
mod q (which B can compute)
= yB
xA
mod q (which A can compute)
 KAB is used as session key in private-key
encryption scheme between Alice and Bob
 if Alice and Bob subsequently communicate,
they will have the same key as before, unless
they choose new public-keys
 attacker needs an x, must solve discrete log

13. Diffie-Hellman Key Exchange
Bob
B
Bob
B
Alice
A
Alice
A
Public Parameters:
large prime q
primitive root a
Choose a secret XA
Compute YA = a
XA
mod q
Send YA
Choose a secret XB
Compute YB = a
XB
mod q
Send YB
Shared Key
KAB
= YB
XA
= a
X
B
XA mod q
Shared Key
KAB
= YA
X
B
= a
X
A
XB mod q

14. Diffie-Hellman Example
 users Alice & Bob who wish to swap keys:
 agree on prime q=353 and a=3
 select random secret keys:
 A chooses xA=97, B chooses xB=233
 compute respective public keys:

yA=3
97
mod 353 = 40 (Alice)

yB=3
233
mod 353 = 248 (Bob)
 compute shared session key as:

KAB= yB
xA
mod 353 = 248
97
= 160 (Alice)

KAB= yA
xB
mod 353 = 40
233
= 160 (Bob)

15. Key Exchange Protocols
 users could create random private/public
D-H keys each time they communicate
 users could create a known private/public
D-H key and publish in a directory, then
consulted and used to securely
communicate with them
 both of these are vulnerable to a meet-in-
the-Middle Attack
 authentication of the keys is needed

16. Man-in-the-Middle Attack
Man-in-the-Middle Attack
Alice
A
Alice
A
Bob
B
Bob
B
Darth
(Attacker)
Darth
(Attacker)
Man-in-the-middle attacker shared
a key between Alice and Bob.

17. Man-in-the-Middle Attack
1. Darth prepares by creating two private / public keys
2. Alice transmits her public key to Bob
3. Darth intercepts this and transmits his first public key to
Bob. Darth also calculates a shared key with Alice
4. Bob receives the public key and calculates the shared key
(with Darth instead of Alice)
5. Bob transmits his public key to Alice
6. Darth intercepts this and transmits his second public key
to Alice. Darth calculates a shared key with Bob
7. Alice receives the key and calculates the shared key (with
Darth instead of Bob)
 Darth can then intercept, decrypt, re-encrypt, forward all
messages between Alice & Bob

18. ElGamal Cryptography
 public-key cryptosystem related to D-H
 so uses exponentiation in a finite (Galois)
 with security based difficulty of computing
discrete logarithms, as in D-H
 each user (eg. A) generates their key
 chooses a secret key (number): 1 < xA < q-1

compute their public key: yA = a
xA
mod q

19. ElGamal Message Exchange
 Bob encrypt a message to send to A computing

represent message M in range 0 <= M <= q-1
• longer messages must be sent as blocks

chose random integer k with 1 <= k <= q-1
 compute one-time key K = yA
k
mod q
 encrypt M as a pair of integers (C1,C2) where
• C1 = a
k
mod q ; C2 = KM mod q
 A then recovers message by
 recovering key K as K = C1
xA
mod q
 computing M as M = C2 K-1
mod q
 a unique k must be used each time

otherwise result is insecure

20. ElGamal Crypto System
Bob
B
Bob
B
Alice
A
Alice
A
Public Parameters:
large prime q
primitive root a
Choose a secret XA
Compute YA = a
XA
mod q
Send YA
Choose a secret XB
Compute K = YA
XB
mod q
Compute YB = a
XB
mod q
Send YB and C = K.M mod q
Shared Key
KAB
= YB
XA
= a
X
B
XA mod q
Shared Key KAB
= YA
X
B
X
A
XB

21. ElGamal Example
 use field GF(19) q=19 and a=10
 Alice computes her key:

A chooses xA=5 & computes yA=10
5
mod 19 = 3
 Bob send message m=17 as (11,5) by

chosing random k=6
 computing K = yA
k
mod q = 3
6
mod 19 = 7
 computing C1 = a
k
mod q = 10
6
mod 19 = 11;
C2 = KM mod q = 7.17 mod 19 = 5
 Alice recovers original message by computing:

recover K = C1
xA
mod q = 11
5
mod 19 = 7

compute inverse K-1
= 7-1
= 11
 recover M = C2 K-1
mod q = 5.11 mod 19 = 17

22. 2222
ElGamal Digital Signature
 Zp* = <g>, m ∈ Zp message

A signs message m.
 Alice: A = ga
, public key = (p, g,A), secret key = x.
 Alice: k random with gcd(k,p-1)=1

r = gk
(mod p)

s = (m – xr)(1/k) mod p-1 [m = sk + xr (mod p-1)]

Signature = (r,s)

Verify gm
=rs
hr

23. 2323
ElGamal Public Key Cryptosystem
and Digital Signature Scheme
 Example
1. P=23, g=5.
2. x=3, then y=10 (for 53
mod 23=10 ).
3. Sign for the message M=8.
4. Select k=5 between 1 and 22 (P-1).
5. Compute r = gk
mod P = 55
mod 23 = 20.
6. Compute s = k-1
(M-xr) mod (P-1) = 5-1
(8-3×20) mod 22 = 9×14
mod 22 = 16.
7. Verification:
gM
= 58
mod 23 =16
(rs
)(yr
) mod P = 2016
× 1020
mod 23= 13×3 mod 23 = 16.