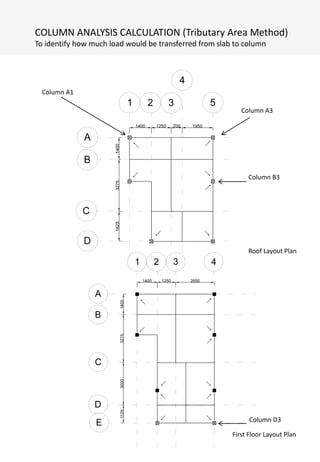
This document describes a student's proposed extension to an existing reinforced concrete structure. The student proposes adding a two-story extension with a garage, gym, library, and wine storage on the ground and first floors. Dead and live loads are quantified for each structural component. Beam analysis is conducted to size structural members, including calculating reactions, shear forces, and bending moments. Load diagrams are provided to illustrate load distribution and transfer from slabs to beams.

1. Building Structures (ARC 2522)
Extension of a R.C Structure
Name: Lee Yiang Siang
Student ID: 0302966
Lecturer: Mr. Mohd Adib Ramli
Chosen Existing R.C Building:
No. 4, Jalan SS1/34, Seksyen 26, Petaling
Jaya, 46300 Sea Park, Selangor.

2. INTRODUCTION
In this project, we are introduced to structural theory, force calculation and basic
structural proposal. We are allowed to understand and gain demonstration of
knowledge of building structure by exposing to the component involved.
After the site visit to the our case study, documentation of measurement drawings
are done to identify the structural elements of the building. The next step is to
propose a renovation works or extension on the existing building . Through
designing extension of this reinforced concrete bungalow, we are able to recognize,
execute and implement basic procedures of building structure design.
In this project, each individual is assigned to design the extension by selecting
appropriate structural members to frame the extension. Load acting on the
structure is identified and quantified after the design is done. The structure is then
analyzed to determine the sizing of structural components.

3. DESIGN BRIEF
An extension is proposed based on the requirement and the area is not to exceed
100m². The extension is extended sideway of two storeys height to enlarge the
compound of the house and provide more activity space to the user.
At the ground floor, a garage is proposed to provide a shelter for the user’s car to
prevent exposure to the violent sunlight and rainwater. A gymnasium next to the
garage is proposed to provide an exercise space for the user. Furthermore on the
first floor, a library is proposed next to the bedroom which provide privacy for user
to enjoy his reading time. Behind the library, there will be a wine storage for user to
keep and collect his wines. In addition, a new balcony is added next to the library
which allows user to relax after reading.

4. PROPOSAL OF EXTENSION
MATERIAL USED AND DENSITY
-Concrete: 24kN/m²
-Brickwall: 19kN/m²
EXTENDED AREA
-Original ground floor area: 190.78m²
-Extended ground floor area: 45.6m²
-Original first floor area: 125.75m²
-Extended first floor area: 45.6m²
-Total floor area: 316.53m²
-Total extended floor area: 91.2m²

5. QUANTIFY DEAD LOADS
ACTING ON STRUCTURE
GROUND FLOOR
Gymnasium:
-Slab thickness= 150mm
-Slab self weight= 0.15 x 24kN/ m3
= 3.6kN/ m3
Garage:
-Slab thickness= 150mm
-Slab self weight= 0.15 x 24kN/ m3
= 3.6kN/ m3
FIRST FLOOR
Wine storage:
-Slab thickness= 150mm
-Slab self weight= 0.15 x 24kN/ m3
= 3.6kN/ m3
Library:
-Slab thickness= 150mm
-Slab self weight= 0.15 x 24kN/ m3
= 3.6kN/ m3
Balcony:
-Slab thickness= 100mm
-Slab self weight= 0.1 x 24kN/ m3
=2.4kN/ m3
BRICK WALL (ground floor) BRICK WALL (first floor)
=wall height x thickness x density =wall height x thickness x density
=3.65m x 0.15 x 19kN/ m3 =3.2m x 0.15 x 19kN/ m3
=10.4kN/ m =9.12kN/ m
BEAM SELF WEIGHT
=beam size x concrete density
=0.15m x 0.45m x 24kN/m3
=1.62kN/m
GROUND FLOOR
Gymnasium:
2.0kN/ m2
Garage:
2.5kN/ m3
FIRST FLOOR
Wine storage:
2.0kN/ m3
Library:
2.5kN/ m3
Balcony:
1.5kN/ m3
QUANTIFY LIVE LOADS
ACTING ON STRUCTURE

6. Ground floor plan
First floor plan
EXTENSION PLAN
A A
A A

7. Roof plan
Proposed
extension
Section A-A

8. EXTENSION STRUCTURAL PLAN
Structural foundation plan Ground floor structural plan
First floor structural plan Rooftop structural plan

9. Balcony
Library
Wine storage
Garage
Gymnasium
FRAME AND SPACE LEGEND

10. IDENTIFY ONE WAY SLAB OR TWO WAY SLAB
Indicating the distribution of load from slab to beam
Ly= Longer side of slab
Lx= Shorter side of slab
When Ly / Lx >2 or =2, it is a one way slab.
When Ly / Lx <2, it is a two way slab.
Gymnasium
=(3900 + 1400)/ 2800
=1.89 (two way slab)
Garage
=3900/ 1500
=2.6 (one way slab)
=4500/ 3900
=1.15 (two way slab)
Wine storage
=2800/ (1400 + 1250)
=1.05 (two way slab)
=2800/ 2650
=1.05 (two way slab)
Library
=(1250 + 2650)/ (2250 + 1500)
=1.04 (two way slab)
Balcony
=(1250 + 2650)/ (2250)
=1.73 (two way slab)
Ground floor structural plan
Garage
Gymnasium
Wine storage
Library
Balcony
First floor structural plan

11. Ground floor structural plan
First floor structural plan
LOAD DISTRIBUTION DIAGRAM

12. BEAM ANALYSIS CALCULATION
Ground Floor Beam, C / 2 - 3
1. Carries self weight – Dead load
2. Slab dead load & Live load
> B – C / 2 – 3 (one way slab)
> C – D / 2 – 3 (two way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 2 - 3 / C in a UDL form.
Dead load from slab B – C / 2 – 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (1.5 / 2)
= 2.7 kN/ m
Dead load on slab C – D / 2 – 3 (garage) (two way slab)
Load is transferred to beam 3 / A – D in a triangular form.
Dead load from slab C – D / 2 – 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (3.9 / 2)
= 7.02 kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Dead load from slab C – D / 2 – 3 = (2/3) (7.02)
= 4.68 kN/m

13. Total Dead Load
Total for 2 – 3 = Beam self weight + Brick wall weight + B - C slab + C – D slab
= 1.62 + 10.4 + 2.7 + 4.68
= 19.4 kN/m
Total Dead Load Diagram

14. Live load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 2 - 3 / C in a UDL form.
Live load from slab B – C / 2 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (1.5 / 2)
= 1.875 kN/ m
Live load on slab C – D / 2 – 3 (garage) (two way slab)
Load is transferred to beam 3 / A – D in a triangular form.
Live load from slab C – D / 2 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (3.9 / 2)
= 4.875 kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Live load from slab C – D / 2 – 3 = (2/3) (4.875)
= 3.25 kN/m
Total Live Load
Total for 1 – 3 = B - C slab + C – D slab
= 1.875 + 3.25
= 5.125

15. Total Live Load Diagram

16. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load 2 – 3 = 19.4 x 1.4
= 27.16 kN/ m
Live load 2 – 3 = 5.125 x 1.6
= 8.2 kN/ m
Ultimate load 2 – 3 = 27.16 kN/ m + 8.2 kN/ m
= 35.36 kN/ m
Ultimate Load Diagram

17. Reactions
Ground floor beam , C / 2 – 3
ΣM2 = 0
= R3Y (3.9) – 35.36 kN/m (3.9) (1.95)
= 3.9R3Y – 268.9 kN
R3Y = 68.9 kN
ΣFY = 0
= R3Y + R2Y – 35.36 kN/m (3.9)
= 68.9 kN + RBY – 137.9 kN
R2Y = 68.9 kN
Load Diagram
Shear force Diagram
Bending Moment Diagram

18. BEAM ANALYSIS CALCULATION
Ground Floor Beam, 2 / B - D
1. Carries self weight – Dead load
2. Slab dead load & Live load
> B – C / 2 – 3 (one way slab)
> C – D / 2 – 3 (two way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 2 - 3 / C in a UDL form.
Dead load from slab B – C / 2 – 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (1.5 / 2)
= 2.7 kN/ m
Dead load on slab C – D / 2 – 3 (garage) (two way slab)
Load is transferred to beam 2 - 3 / C in a trapezoidal form.
Dead load from slab C – D / 2 – 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (3.9 / 2)
= 7.02 kN/ m

19. Total Dead Load
Total for B – C = Beam self weight + Brick wall weight + B – C slab
= 1.62 kN/ m + 10.4kN/m + 2.7 kN/m
= 14.72 kN/ m
Total for C – D = Beam self weight + Brick wall weight + C – D slab
= 1.62 kN/ m + 10.4kN/m + 7.02 kN/m
= 19.04 kN/ m
Total Dead Load Diagram

20. Live load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 2 - 3 / C in a UDL form.
Live load from slab B – C / 2 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (1.5 / 2)
= 1.875 kN/ m
Live load on slab C – D / 2 – 3 (garage) (two way slab)
Load is transferred to beam 2 - 3 / C in a trapezoidal form.
Live load from slab C – D / 2 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (3.9 / 2)
= 4.875 kN/ m
Total Live Load
Total for B – C = 1.875 kN/m
Total for C – D = 4.875 kN/m
Total Live Load Diagram

21. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load B – C = 14.72 x 1.4
= 20.608 kN/m
Dead load C – D = 19.04 x 1.4
= 26.656 kN/m
Live load B – C = 1.875 x 1.6
= 3 kN/m
Live load C – D = 4.875 x 1.6
= 7.8 kN/m
Ultimate load B – C = 20.608 + 3
= 23.608 kN/ m
Ultimate load C – D = 26.656 + 7.8
= 34.456 kN/m
Ultimate Load Diagram

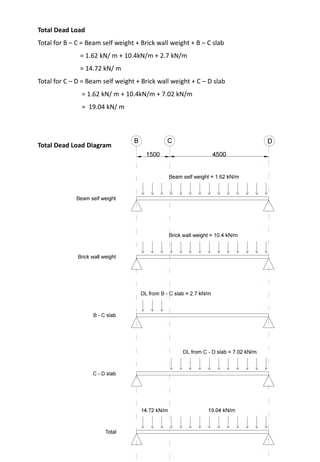
22. Reactions
ΣMB = 0
= RDY (6) – 34.456 (4.5) (3.75) – 23.608 (1.5) (0.75) – [point load (2,C)] (1.5)
= 6RDY – 581.45 – 26.56 – 103.35
RDY = 118.56 kN
ΣFY = 0
= RDY + RBY – 34.456 (4.5) – 23.608 (1.5) – 103.35
= 118.56 + RBY – 293.814
RBY = 175.254 kN
Load Diagram
Shear force Diagram
Bending Moment Diagram

23. BEAM ANALYSIS CALCULATION
Ground Floor Beam, B / 1 - 3
1. Carries self weight – Dead load
2. Slab dead load & Live load
> A – B / 1 – 3 (two way slab)
> B – C / 2 – 3 (one way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab A – B / 1 – 3 (garage) (two way slab)
Load is transferred to beam 1 - 3 / B in a trapezoidal form.
Dead load from slab A – B / 1 – 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (2.8 / 2)
= 5.04 kN/ m
Dead load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 1 - 3 / B in a UDL form.
Dead load from slab B – C / 2 - 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (1.5 / 2)
= 2.7 kN/ m

24. Total Dead Load
Total for 1 – 2 = Beam self weight + Brick wall weight + (1 – 3 slab)
= 1.62 kN/ m + 10.4 kN/m + 5.04 kN/m
= 17.06 kN/ m
Total for 2 – 3 = Beam self weight + Brick wall weight + (1 – 3 slab) + (2 – 3 slab)
= 1.62 kN/ m + 10.4 kN/m + 5.04 kN/m + 2.7 kN/m
= 19.76 kN/ m
Total Dead Load Diagram

25. Live load on slab A – B / 1 – 3 (garage) (two way slab)
Load is transferred to beam 1 - 3 / B in a trapezoidal form.
Live load from slab A – B / 1 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (2.8 / 2)
= 3.5 kN/ m
Live load on slab B – C / 2 – 3 (garage) (one way slab)
Load is transferred to beam 1 - 3 / B in a UDL form.
Live load from slab B – C / 2 – 3 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (1.5 / 2)
= 1.875 kN/ m
Total Live Load
Total for 1 – 2 = (A – B / 1 – 3)
= 3.5 kN/ m
Total for 2 – 3 = (A – B / 1 – 3) + (B – C / 2 – 3)
= 3.5 kN/ m + 1.875 kN/ m
= 5.375 kN/ m

26. Total Live Load Diagram

27. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load 1 - 2 = 17.06 kN/ m x 1.4
= 23.884 kN/ m
Dead load 2 – 3 = 19.76 kN/ m x 1.4
= 27.664 kN/ m
Live load 1 – 2 = 3.5 kN/ m x 1.6
= 5.6 kN/ m
Live load 2 – 3 = 5.375 kN/ m x 1.6
= 8.6 kN/ m
Ultimate load 1 - 2 = 23.884 kN/ m + 5.6 kN/ m
= 29.484 kN/ m
Ultimate load 2 - 3 = 27.664 kN/ m + 8.6 kN/ m
= 36.264 kN/ m
Ultimate Load Diagram

28. Reactions
Ground floor beam : 1 – 3 / B
ΣM1 = 0
= R3Y (5.3) – 36.264 kN/m (3.9) (3.35) – 29.484 kN/m (1.4) (0.7) – 175.254 kN (1.4)
= 5.3R3Y – 473.79 – 28.89 – 245.36
R3Y = 141.14 kN
ΣFY = 0
= R3Y + R1Y – (36.264 kN/m x 3.9m) – ( 29.484 kN/m x 1.4) – 175.254 kN (1.4)
= 129.42 kN + R1Y – 141.43 – 41.28 – 245.36
R1Y = 298.65 kN
Load Diagram
Shear force Diagram
Bending Moment Diagram

29. BEAM ANALYSIS CALCULATION
First Floor Beam, 2 / B - C
1. Carries self weight – Dead load
2. Slab dead load & Live load
> B – C / 2 – 4 (two way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab B – C / 2 – 4 (library) (two way slab)
Load is transferred to beam 2 / B - C in a triangular form.
Dead load from slab B – C / 2 - 4 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (3.75 / 2)
= 6.75 kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Dead load from slab B – C / 2 – 4 = (2/3) (6.75)
= 4.5 kN/m
Total Dead Load
Total for B – C = Beam self weight + Brick wall weight + (B – C slab)
= 1.62 kN/ m + 9.12kN/m + 4.5 kN/m
= 15.24 kN/ m

30. Total Dead Load Diagram

31. Live load on slab B – C / 2 – 4 (library) (two way slab)
Load is transferred to beam 2 / B - C in a triangular form.
Live load from slab B – C / 2 - 4 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (3.75 / 2)
= 4.7kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Live load from slab B – C / 2 – 4 = (2/3) (4.7)
= 3.13 kN/m
Total Live Load
Total for B – C = 3.13 kN/m
Total Live Load Diagram

32. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load B – C = 15.24 kN/ m x 1.4
= 21.336 kN/ m
Live load B – C = 3.13 kN/ m x 1.6
= 5 kN/ m
Ultimate load B - C = 21.336 kN/ m + 5 kN/ m
= 26.336 kN/ m
Ultimate Load Diagram

33. Reactions
Ground floor beam : 2 / B – C
ΣMB = 0
= RCY (3.75) – 26.336 kN/m (3.75) (1.875)
= 3.75RCY – 185.175
RCY = 49.38 kN
ΣFY = 0
= RCY + RBY – (28.128 kN/m x 3.75m)
= 49.38 kN + RBY – 98.76
RBY = 49.38 kN
Load Diagram
Shear force Diagram
Bending Moment Diagram

34. BEAM ANALYSIS CALCULATION
First Floor Beam, 3 / A - B
1. Carries self weight – Dead load
2. Slab dead load & Live load
> A – B / 1 – 3 (two way slab)
> A – B / 3 – 4 (two way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab A – B / 1 – 3 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a trapezoidal form.
Dead load from slab A – B / 1 - 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (2.65 / 2)
= 4.77 kN/ m
Dead load on slab A – B / 3 – 4 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a trapezoidal form.
Dead load from slab A – B / 3 - 4 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (2.65 / 2)
= 4.77 kN/ m

35. Total Dead Load
Total for A – B = Beam self weight + Brick wall weight + (1– 3 slab) + (3 – 4 slab)
= 1.62 kN/ m + 9.12kN/m + 4.77kN/m + 4.77kN/m
= 20.28 kN/ m
Total Dead Load Diagram

36. Live load on slab A – B / 1 – 3 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a trapezoidal form.
Live load from slab A – B / 1 - 3 = Live load on slab x (Lx / 2)
= 2.0 kN/ m2 x (2.65 / 2)
= 2.65kN/ m
Live load on slab A – B / 3 – 4 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a trapezoidal form.
Live load from slab A – B / 3 - 4 = Live load on slab x (Lx / 2)
= 2.0 kN/ m2 x (2.65 / 2)
= 2.65kN/ m
Total Live Load
Total for A - B = (1– 3 slab) + (3 – 4 slab)
= 2.65 + 2.65
= 5.3 kN/m
Total Live Load Diagram

37. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load A – B = 20.28 kN/ m x 1.4
= 28.392 kN/ m
Live load A – B = 5.3 kN/ m x 1.6
= 8.48 kN/ m
Ultimate load A - B = 28.392 kN/ m + 8.48 kN/ m
= 36.87 kN/ m
Ultimate Load Diagram

38. Reactions
Ground floor beam : 3 / A – B
ΣMA = 0
= RBY (2.8) – 36.87 kN/m (2.8) (1.4)
= 2.8RBY – 144.5 kN
RBY = 51.6 kN
ΣFY = 0
= RBY + RAY – (36.87 kN/m x 2.8m)
= 51.6 kN + RAY – 103.24 kN
RAY = 51.636 kN
Load Diagram
Shear force Diagram
Bending Moment Diagram

39. BEAM ANALYSIS CALCULATION
First Floor Beam, B / 1 - 4
1. Carries self weight – Dead load
2. Slab dead load & Live load
> A – B / 1 – 3 (two way slab)
> A – B / 3 – 4 (two way slab)
> B – C / 2 – 4 (two way slab)
3. Brickwall – Dead load
Beam self weight = Beam size x concrete density
= 0.15m x 0.45m x 24kN/ m3
= 1.62kN/ m
Brick wall weight = wall height x thickness x density
(ground floor) = 3.65m x 0.15 x 19kN/ m3 (first floor) = 3.2m x 0.15 x 19kN/ m3
= 10.4kN/ m = 9.12kN/ m
Dead load on slab A – B / 1 – 3 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a triangular form.
Dead load from slab A – B / 1 - 3 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (2.65 / 2)
= 4.77 kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Dead load from slab A – B / 1 – 3 = (2/3) (4.77)
= 3.18 kN/m
Dead load on slab A – B / 3 – 4 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a triangular form.
Dead load from slab A – B / 3 - 4 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (2.65 / 2)
= 4.77 kN/ m

40. Convert triangular load to UDL by applying a factor of 2/3.
Dead load from slab A – B / 3 – 4 = (2/3) (4.77)
= 3.18 kN/m
Dead load on slab B – C / 2 – 4 (library) (two way slab)
Load is transferred to beam 3 / A - B in a trapezoidal form.
Dead load from slab B – C / 2 - 4 = Dead load on slab x (Lx / 2)
= 3.6 kN/ m2 x (3.75 / 2)
= 6.75 kN/ m
Total Dead Load
Total for 1 – 2 = Beam self weight + Brick wall weight + (1– 3 slab)
= 1.62 kN/ m + 9.12kN/m + 3.18 kN/m
= 13.92 kN/ m
Total for 2 – 3 = Beam self weight + Brick wall weight + (1– 3 slab) + (2 – 4 slab)
= 1.62 kN/ m + 9.12kN/m + 3.18 kN/m + 6.75 kN/m
= 20.67 kN/ m
Total for 3 – 4 = Beam self weight + Brick wall weight + (2– 4 slab) + (3 – 4 slab)
= 1.62 kN/ m + 9.12kN/m + 6.75 kN/m + 3.18 kN/m
= 20.67 kN/ m

41. Total Dead Load Diagram

42. Live load on slab A – B / 1 – 3 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a triangular form.
Live load from slab A – B / 1 - 3 = Live load on slab x (Lx / 2)
= 2.0 kN/ m2 x (2.65 / 2)
= 2.65kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Live load from slab A – B / 1 – 3 = (2/3) (2.65)
= 1.77kN/m
Live load on slab A – B / 3 – 4 (wine storage) (two way slab)
Load is transferred to beam 3 / A - B in a triangular form.
Live load from slab A – B / 3 - 4 = Live load on slab x (Lx / 2)
= 2.0 kN/ m2 x (2.65 / 2)
= 2.65kN/ m
Convert triangular load to UDL by applying a factor of 2/3.
Live load from slab A – B / 1 – 3 = (2/3) (2.65)
= 1.77kN/m
Live load on slab B – C / 2 – 4 (library) (two way slab)
Load is transferred to beam 3 / A - B in a triangular form.
Live load from slab B – C / 2 - 4 = Live load on slab x (Lx / 2)
= 2.5 kN/ m2 x (3.75 / 2)
= 4.69 kN/ m
Total Live Load
Total for 1 – 2 = 1– 3 slab
= 1.77 kN/m
Total for 2 – 3 = 1 – 3 slab + 2 – 4 slab
= 1.77 kN/m + 4.69 kN/m
= 6.46 kN/ m
Total for 3 – 4 = 3 – 4 slab + 2 – 4 slab
= 1.77 kN/m + 4.69 kN/m
= 6.46 kN/m

43. Total Live Load Diagram

44. Ultimate load
Apply factor 1.4 and 1.6 to dead load and live load respectively.
Dead load 1 – 2 = 13.92 kN/ m x 1.4
= 19.488 kN/ m
Dead load 2 – 3 = 20.67 kN/ m x 1.4
= 28.938 kN/ m
Dead load 3 – 4 = 20.67 kN/ m x 1.4
= 28.938 kN/ m
Live load 1 – 2 = 1.77kN/ m x 1.6
= 2.832 kN/ m
Live load 2 – 3 = 6.46kN/ m x 1.6
= 10.336 kN/ m
Live load 3 – 4 = 6.46kN/ m x 1.6
= 10.336 kN/ m
Ultimate load 1 - 2 = 19.488 kN/ m + 2.832 kN/ m
= 22.32kN/ m
Ultimate load 2 - 3 = 28.938 kN/ m + 10.336 kN/ m
= 39.274kN/ m
Ultimate load 2 - 3 = 28.938 kN/ m + 10.336 kN/ m
= 39.274kN/ m
Ultimate Load Diagram

45. Reactions
Ground floor beam : B / 1 – 4
ΣM1 = 0
= R4Y (5.3) – 39.274 kN/m (2.65) (3.975) – 39.274 kN/m (1.25) (2.025) – 22.32
kN/m (1.4) (0.7) – (point load 2,B)(1.4) – (point load 3,B) (2.65)
= 5.3R4Y – 413.7kN – 99.4kN – 21.87kN – 49.38 (1.4) – 51.6kN (2.65)
= 5.3R4Y – 534.97 – 69.132 – 136.74
R4Y = 139.78kN
ΣFY = 0
= R4Y + R1Y – 39.724 (2.65) – 39.724 (1.25) – 22.32 (1.4) – 69.132 – 136.74
= 139.78 kN + R1Y – 105.27kN – 49.66kN – 31.25 - 205.872
R1Y = 252.272kN

46. Load Diagram
Shear force Diagram
Bending Moment Diagram

47. COLUMN ANALYSIS CALCULATION (Tributary Area Method)
To identify how much load would be transferred from slab to column
Roof Layout Plan
First Floor Layout Plan
Column A1
Column A3
Column B3
Column D3

48. Ground Floor Layout Plan

49. COLUMN ANALYSIS CALCULATION (Tributary Area Method)
To identify how much load would be transferred from slab to column
Column A/1
Dead Load
Roof
Flat Roof Slab
Slab thickness = 200 mm
Slab self-weight
=0.20mx24kN/m3
=4.8kN/m2
Area = 1.4 m x 2.65 m = 3.71 m2
Dead Load of Flat Roof Slab
=4.8kN/m2 x3.5m2
= 16.8 kN
Beam Self-Weight
=1.62kN/m2 x(1.4m+2.65m)
= 6.65 kN
TOTAL DEAD LOAD OF ROOF
= 16.8 kN + 6.65 kN
= 23.45 kN
First Floor
Slab (Wine Storage)
=3.6kN/m2 x(1.4 m x 2.65 m)
= 13.356kN
Beam Self-Weight
= 1.62 kN/m x (1.4m+2.65m)
= 6.561kN
Brick Wall
= 9.12 kN/m x (1.4m+2.65m)
= 36.9 kN
TOTAL DEAD LOAD OF FIRST FLOOR
= 13.356 kN + 6.561 kN + 36.9 kN
=56.817 kN
Ground Floor
Slab (Gymnasium)
=3.6kN/m2 x(1.4 m x 2.65 m)
= 13.356 kN
Beam Self-Weight
=1.62kN/mx(1.4m+2.65m)
= 6.561 kN
Brick Wall
= 9.12 kN/m x (1.4m+2.65m)
= 36.94 kN
TOTAL DEAD LOAD OF GROUND FLOOR
= 13.356kN + 6.561 kN + 36.94 kN
= 56.857 kN
TOTAL DEAD LOAD FROM ROOF TO
FOUNDATION
23.45 kN + 56.817 kN + 56.857 kN
= 137.124 kN

50. Live Load
Roof
Live Load of Flat Roof Slab
= 0.5 kN/m2 x 3.71 m2
= 1.75 kN
First Floor
Slab (Wine Storage)
=2.0 kN/m2 x(3.71 m2)
= 7.42 kN
Ground Floor
Slab (Gymnasium)
= 2.0 kN/ m2 x (3.71 m2)
= 7.42 kN
TOTAL LIVE LOAD FROM ROOF TO
FOUNDATION
1.75 kN + 7.42 kN + 7.42 kN
= 16.59 kN
Ultimate Load
137.124 kN x 1.4 + 16.59 kN x 1.6
= 191.97 kN + 26.544 kN
= 218.514
Assumption
fcu = 30 N/mm2 (concrete strength)
fy = 250 N/mm2 (yield strength of steel)
Ac = 150 x 150 = 22500mm2 (cross section
of concrete column)
Asc = 22500 mm2 x 2 % = 450 mm2 (steel
content in a column)
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (22500 ) + 0.8 (450 ) (250)
= 360000 N
= 360 kN
Conclusion
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (120x 120) + 0.8 (120 x 120 x 2%) (250)
= 230.4 kN
The suitable size of column A/1 is
120 mm x 120 mm, which can sustain
ultimate load of 218.514 kN.

51. COLUMN ANALYSIS CALCULATION (Tributary Area Method)
To identify how much load would be transferred from slab to column
Column A/3
Dead Load
Roof
Flat Roof Slab
Slab thickness = 200 mm
Slab self-weight
=0.20mx24kN/m3
=4.8kN/m2
Area = 1.4 m x 2.65 m = 3.71 m2
Dead Load of Flat Roof Slab
=4.8kN/m2 x3.5m2
= 16.8 kN
Beam Self-Weight
=1.62kN/m2 x(1.4m+2.65m)
= 6.65 kN
TOTAL DEAD LOAD OF ROOF
= 16.8 kN + 6.65 kN
= 23.45 kN
First Floor
Slab (Wine Storage)
=3.6kN/m2 x(1.4 m x 2.65 m)
= 13.356kN
Beam Self-Weight
= 1.62 kN/m x (1.4m+2.65m)
= 6.561kN
Brick Wall
= 9.12 kN/m x (1.4m+2.65m)
= 36.9 kN
TOTAL DEAD LOAD OF FIRST FLOOR
= 13.356 kN + 6.561 kN + 36.9 kN
=56.817 kN
Ground Floor
Slab (Gymnasium)
=3.6kN/m2 x(1.4 m x 2.65 m)
= 13.356 kN
Beam Self-Weight
=1.62kN/mx(1.4m+2.65m)
= 6.561 kN
Brick Wall
= 9.12 kN/m x (1.4m+2.65m)
= 36.94 kN
TOTAL DEAD LOAD OF GROUND FLOOR
= 13.356kN + 6.561 kN + 36.94 kN
= 56.857 kN
TOTAL DEAD LOAD FROM ROOF TO
FOUNDATION
23.45 kN + 56.817 kN + 56.857 kN
= 137.124 kN

52. Live Load
Roof
Live Load of Flat Roof Slab
= 0.5 kN/m2 x 3.71 m2
= 1.75 kN
First Floor
Slab (Wine Storage)
=2.0 kN/m2 x(3.71 m2)
= 7.42 kN
Ground Floor
Slab (Gymnasium)
= 2.0 kN/ m2 x (3.71 m2)
= 7.42 kN
TOTAL LIVE LOAD FROM ROOF TO
FOUNDATION
1.75 kN + 7.42 kN + 7.42 kN
= 16.59 kN
Ultimate Load
137.124 kN x 1.4 + 16.59 kN x 1.6
= 191.97 kN + 26.544 kN
= 218.514
Assumption
fcu = 30 N/mm2 (concrete strength)
fy = 250 N/mm2 (yield strength of steel)
Ac = 150 x 150 = 22500mm2 (cross section
of concrete column)
Asc = 22500 mm2 x 2 % = 450 mm2 (steel
content in a column)
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (22500 ) + 0.8 (450 ) (250)
= 360000 N
= 360 kN
Conclusion
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (120x 120) + 0.8 (120 x 120 x 2%) (250)
= 230.4 kN
The suitable size of column A/3 is
120 mm x 120 mm, which can sustain
ultimate load of 218.514 kN.

53. COLUMN ANALYSIS CALCULATION (Tributary Area Method)
To identify how much load would be transferred from slab to column
Column B/3
Dead Load
Roof
Flat Roof Slab
Slab thickness = 200 mm
Slab self-weight
=0.20mx24kN/m3
=4.8kN/m2
Area = 3.275 m x 2.65 m = 8.68 m2
Dead Load of Flat Roof Slab
=4.8kN/m2 x3.5m2
= 16.8 kN
Beam Self-Weight
=1.62kN/m2 x(3.275 m+2.65m)
= 9.6 kN
TOTAL DEAD LOAD OF ROOF
= 16.8 kN + 9.6 kN
= 161.28 kN
First Floor
Slab (Library)
=3.6kN/m2 x(3.275 m x 2.65 m)
= 31.248 kN
Beam Self-Weight
= 1.62 kN/m x (3.275 m+2.65m)
= 9.6 kN
Brick Wall
= 9.12 kN/m x (3.275 m+2.65m)
= 54.036 kN
TOTAL DEAD LOAD OF FIRST FLOOR
= 31.248 kN + 9.6 kN + 54.036 kN
=94.884 kN
Ground Floor
Slab (Garage)
=3.6kN/m2 x(3.275 m x 2.65 m)
= 31.248 kN
Beam Self-Weight
=1.62kN/mx(3.275 m+2.65m)
= 9.6 kN
Brick Wall
= 10.4 kN/m x (3.275 m+2.65m)
= 61.62 kN
TOTAL DEAD LOAD OF GROUND FLOOR
= 31.248 kN + 9.6 kN + 61.62 kN
= 102.468 kN
TOTAL DEAD LOAD FROM ROOF TO
FOUNDATION
161.28 kN + 94.884 kN + 102.468 kN
= 358.632 kN

54. Live Load
Roof
Live Load of Flat Roof Slab
= 0.5 kN/m2 x 8.68 m2
= 4.34 kN
First Floor
Slab (Library)
=2.5 kN/m2 x(8.68 m2)
= 21.7 kN
Ground Floor
Slab (Garage)
= 2.5 kN/ m2 x (8.68 m2)
= 21.7 kN
TOTAL LIVE LOAD FROM ROOF TO
FOUNDATION
4.34 kN + 21.7 kN + 21.7 kN
= 47.74 kN
Ultimate Load
358.632 kN x 1.4 + 47.74 kN x 1.6
= 502.08 kN + 76.38 kN
= 578.46 kN
Assumption
fcu = 30 N/mm2 (concrete strength)
fy = 250 N/mm2 (yield strength of steel)
Ac = 150 x 150 = 22500mm2 (cross section
of concrete column)
Asc = 22500 mm2 x 2 % = 450 mm2 (steel
content in a column)
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (22500 ) + 0.8 (450 ) (250)
= 360000 N
= 360 kN
Conclusion
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (200 x 200) + 0.8 (200 x 200 x 2%) (250)
= 640 kN
The suitable size of column B/3 is
200 mm x 200 mm, which can sustain
ultimate load of 578.46 kN.

55. COLUMN ANALYSIS CALCULATION (Tributary Area Method)
To identify how much load would be transferred from slab to column
Column D/3
Column ends at first floor.
Dead Load
First Floor
Slab (Balcony)
=2.4kN/m2 x(1.95 m x 1.125 m)
= 5.265 kN
Beam Self-Weight
= 1.0 kN/m x (1.95 m+ 1.125 m)
= 3.075 kN
TOTAL DEAD LOAD OF FIRST FLOOR
= 5.265 kN + 3.075 kN
= 8.34 kN
Ground Floor
Slab (Garage)
=3.6kN/m2 x(1.95 m x 3.0 m)
= 21.06 kN
Beam Self-Weight
=1.62kN/mx(1.95 m+ 3.0 m)
= 8.019 kN
Brick Wall
= 10.4 kN/m x (1.95 m+3.0 m)
= 51.48 kN
TOTAL DEAD LOAD OF GROUND FLOOR
= 21.06 kN + 8.019 kN + 51.48 kN
= 80.56 kN
TOTAL DEAD LOAD FROM FIRST FLOOR TO
FOUNDATION
8.34 kN + 80.56 kN
= 88.9 kN

56. Live Load
First Floor
Slab (Balcony)
=1.5 kN/m2 x(2.19 m2)
= 3.285 kN
Ground Floor
Slab (Garage)
= 2.5 kN/ m2 x (2.19 m2)
= 5.475 kN
TOTAL LIVE LOAD FROM FIRST
FLOOR TO FOUNDATION
3.285 kN + 5.475 kN
= 8.76 kN
Ultimate Load
88.9 kN x 1.4 + 8.76 kN x 1.6
= 124.46 kN + 14.016 kN
= 138.476 kN
Assumption
fcu = 30 N/mm2 (concrete strength)
fy = 250 N/mm2 (yield strength of steel)
Ac = 150 x 150 = 22500mm2 (cross section
of concrete column)
Asc = 22500 mm2 x 2 % = 450 mm2 (steel
content in a column)
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (22500 ) + 0.8 (450 ) (250)
= 360000 N
= 360 kN
Conclusion
N (capacity of concrete)
= 0.4 fcuAc + 0.8 Ascfy
= 0.4 (30) (100 x 100) + 0.8 (100 x 100 x 2%) (250)
= 160 kN
The suitable size of column D/3 is
100 mm x 100 mm, which can sustain
ultimate load of 138.476 kN.

57. REFERENCES:
Adib, M.R. (2014). Lecture Slides: Beams Part 2. Retrieved 11 June from
https://times.taylors.edu.my/pluginfile.php/1521481/mod_resource/content/1/Beams
%20Part%202.pdf
Ann S.P. (2014). Part 1: Frame It Up. Retrieved 11 June from
http://www.powtoon.com/p/euyoG1UdTcD/
Ann S.P. (2014). Part 2: Quantify Loads. Retrieved 11 June from
http://www.powtoon.com/p/dyVdvydgVOY/
Ann S.P. (2014). Part 3: Distributing Load from Slab to Beam. Retrieved 11 June from
http://www.powtoon.com/p/eQ0DDLd4PWg/
Ann S.P. (2014). Part 4: Load Diagram from Beam. Retrieved 12 June from
http://www.powtoon.com/p/foCn6KNsJx1/
MCD Legal Advisers. (2006). Uniform Buildings By-Laws. Malaysia: MCD Publishers.
Retrieved 13June from http://www.scribd.com/doc/30457115/13282147-Uniform-
Building-by-Laws