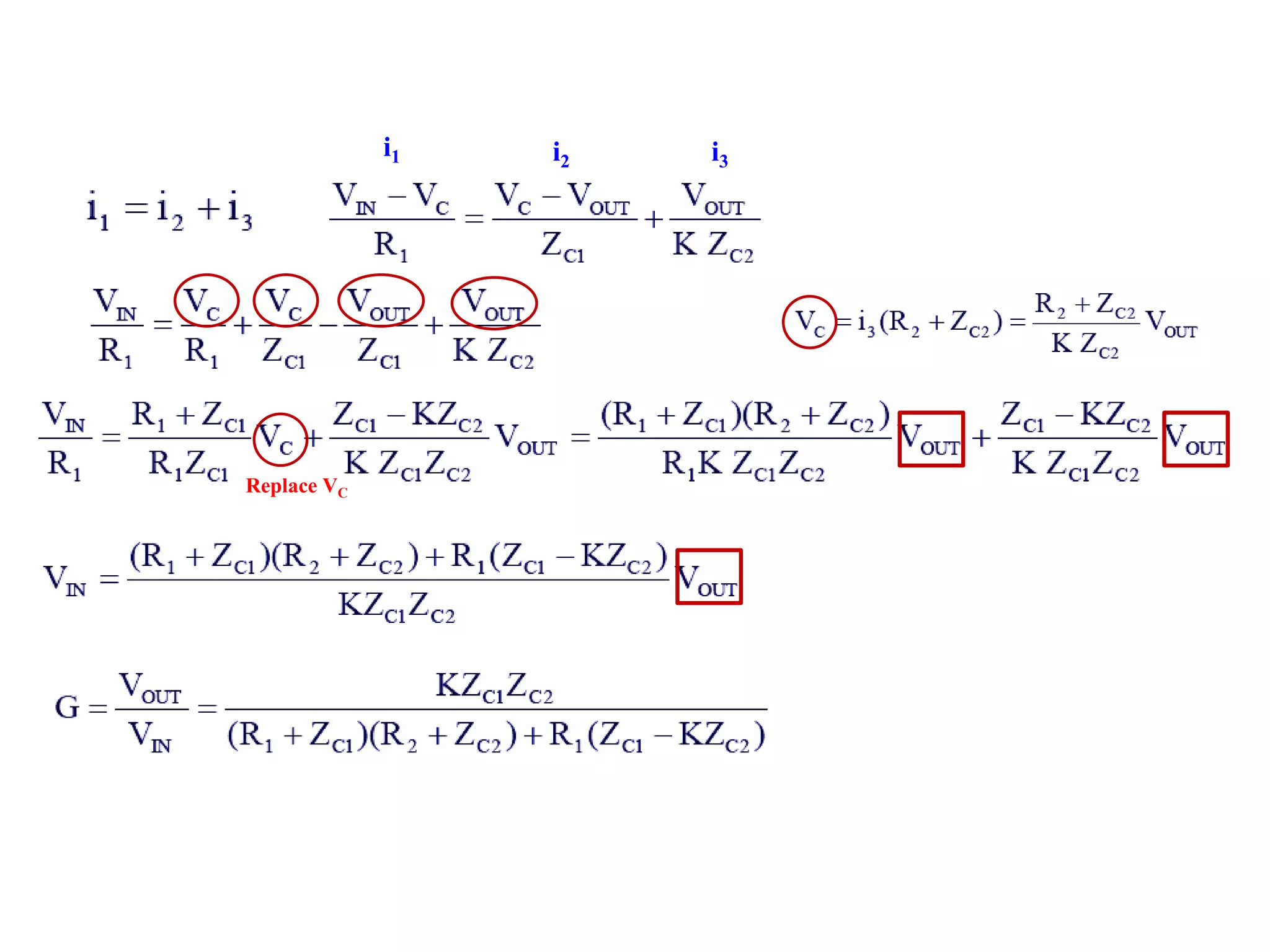
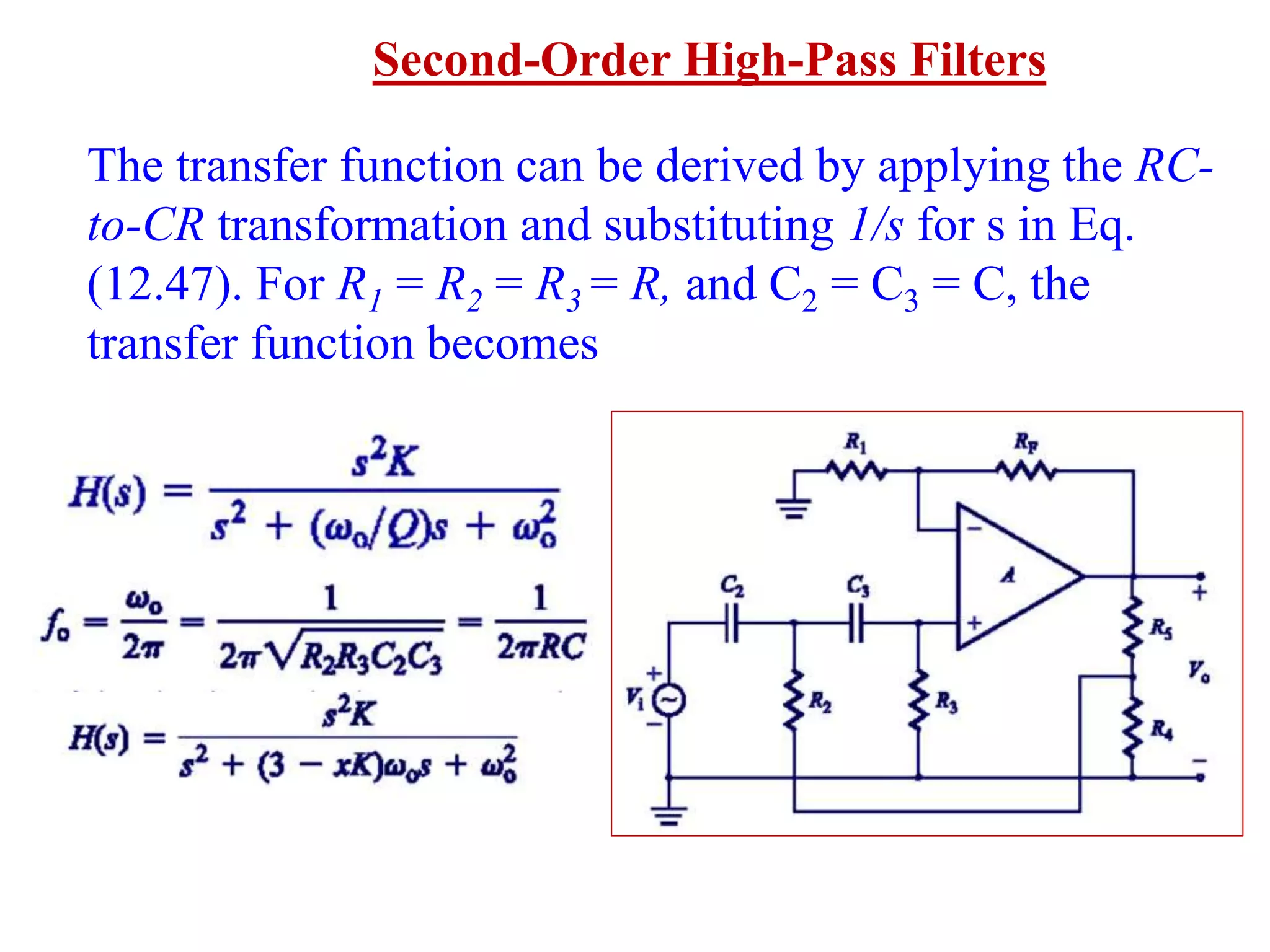
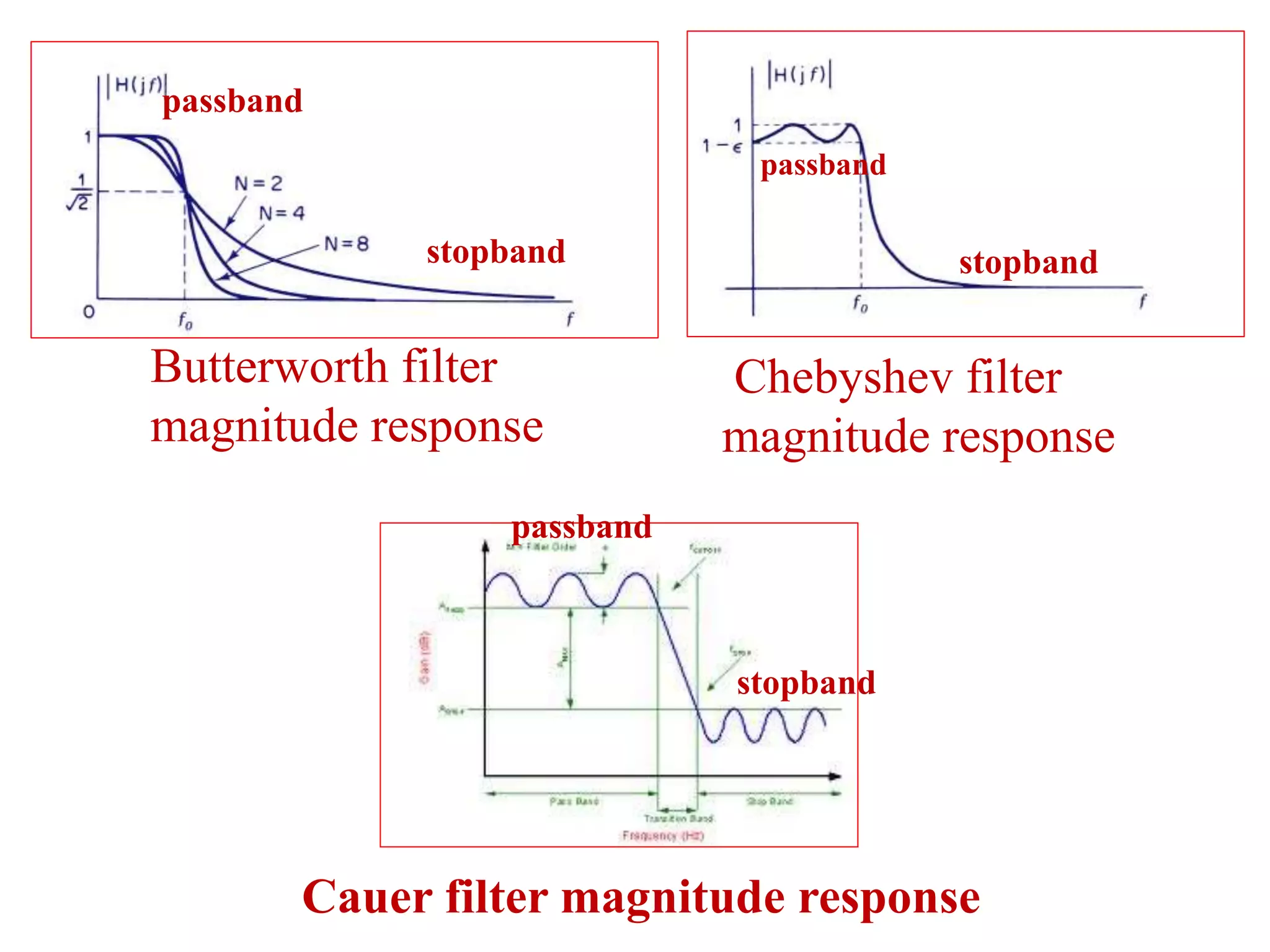
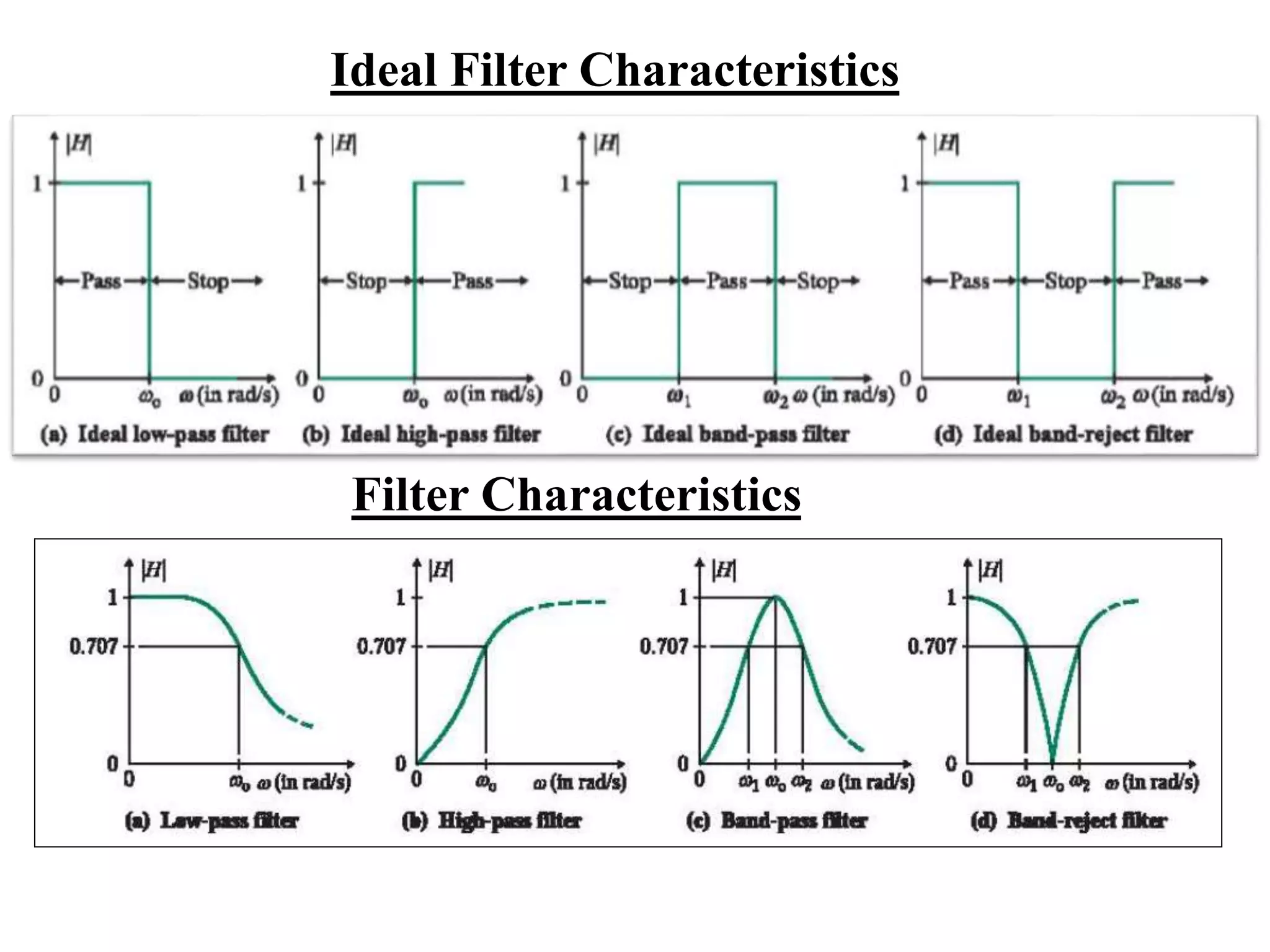
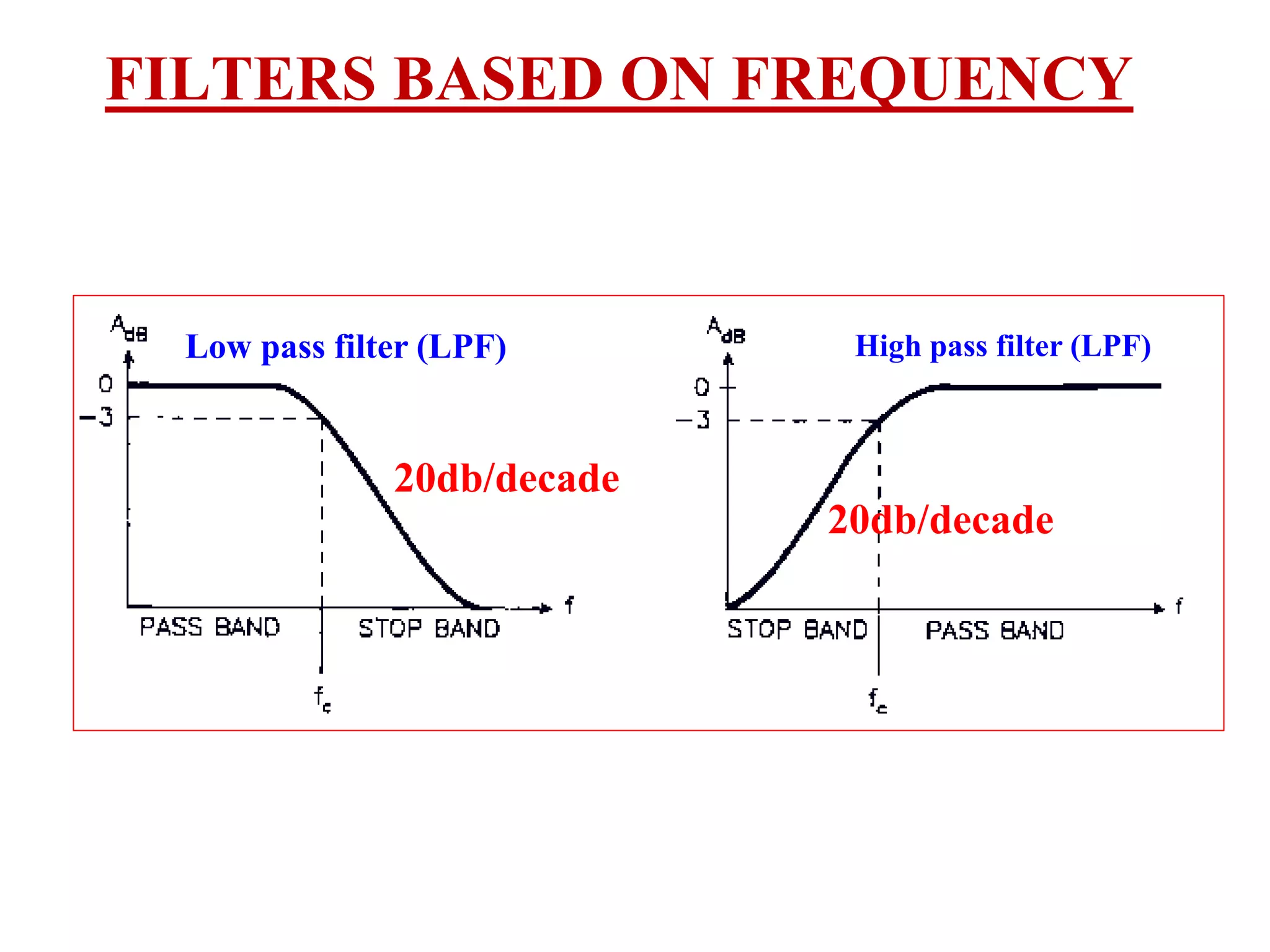
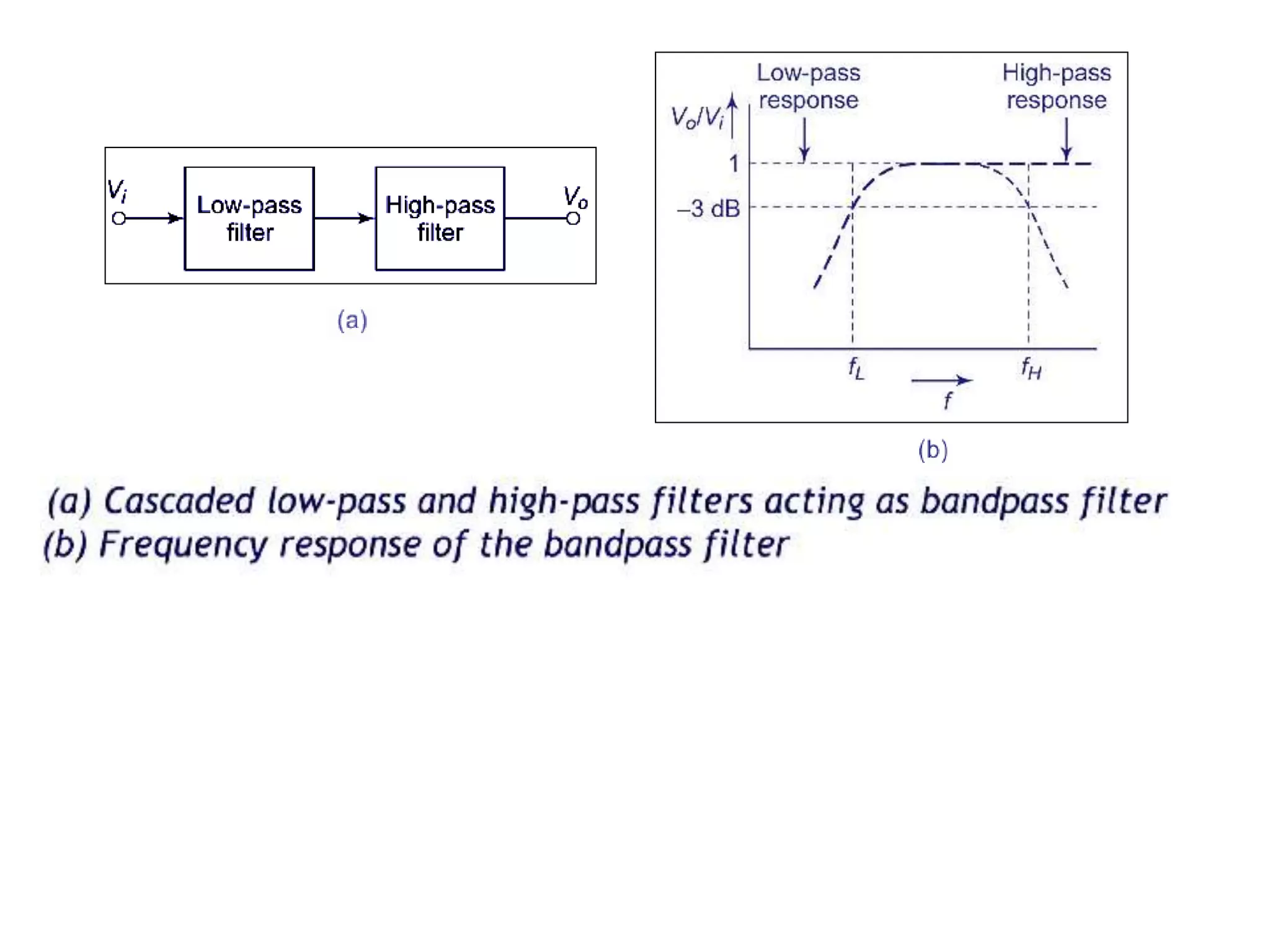
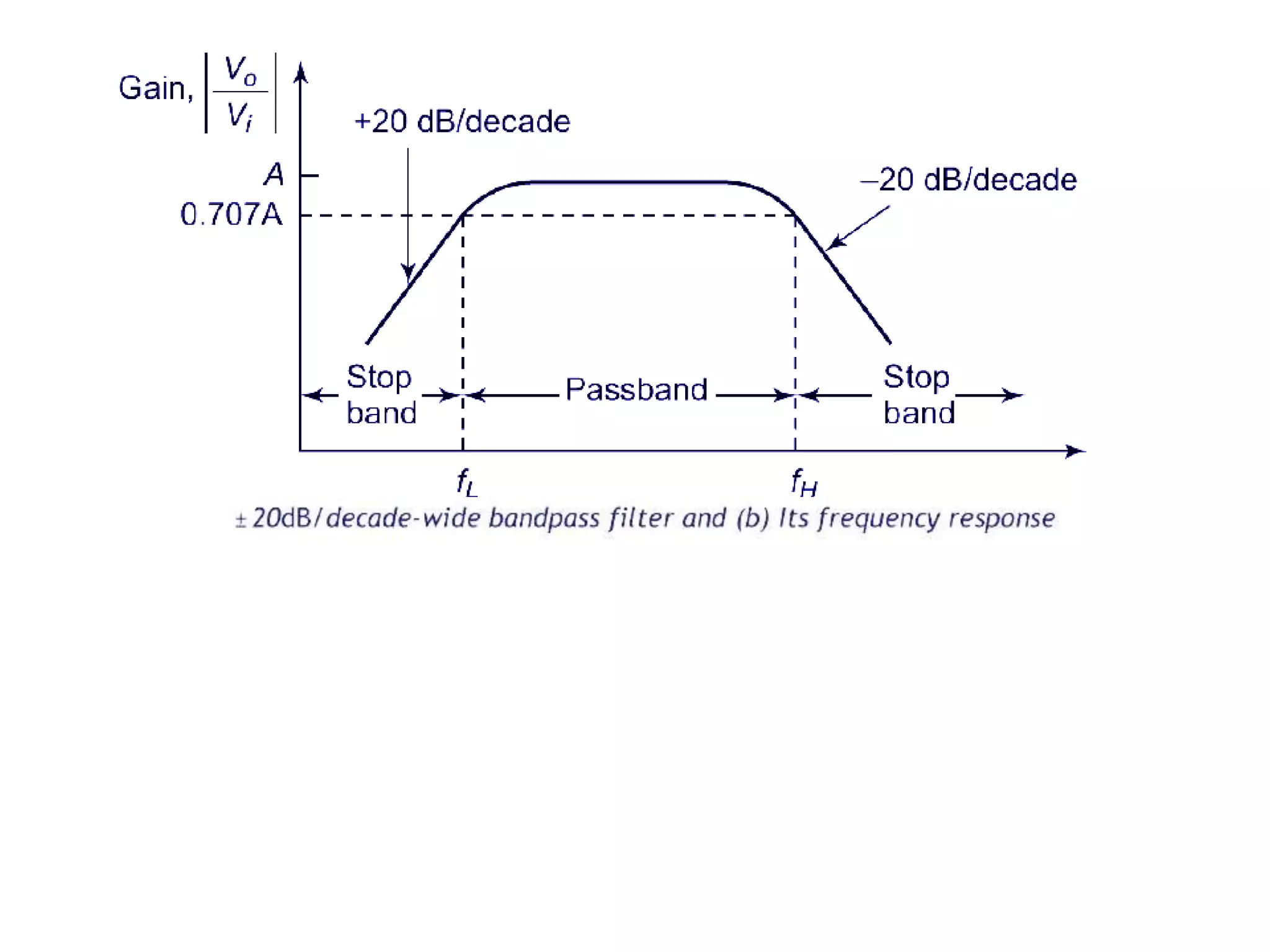
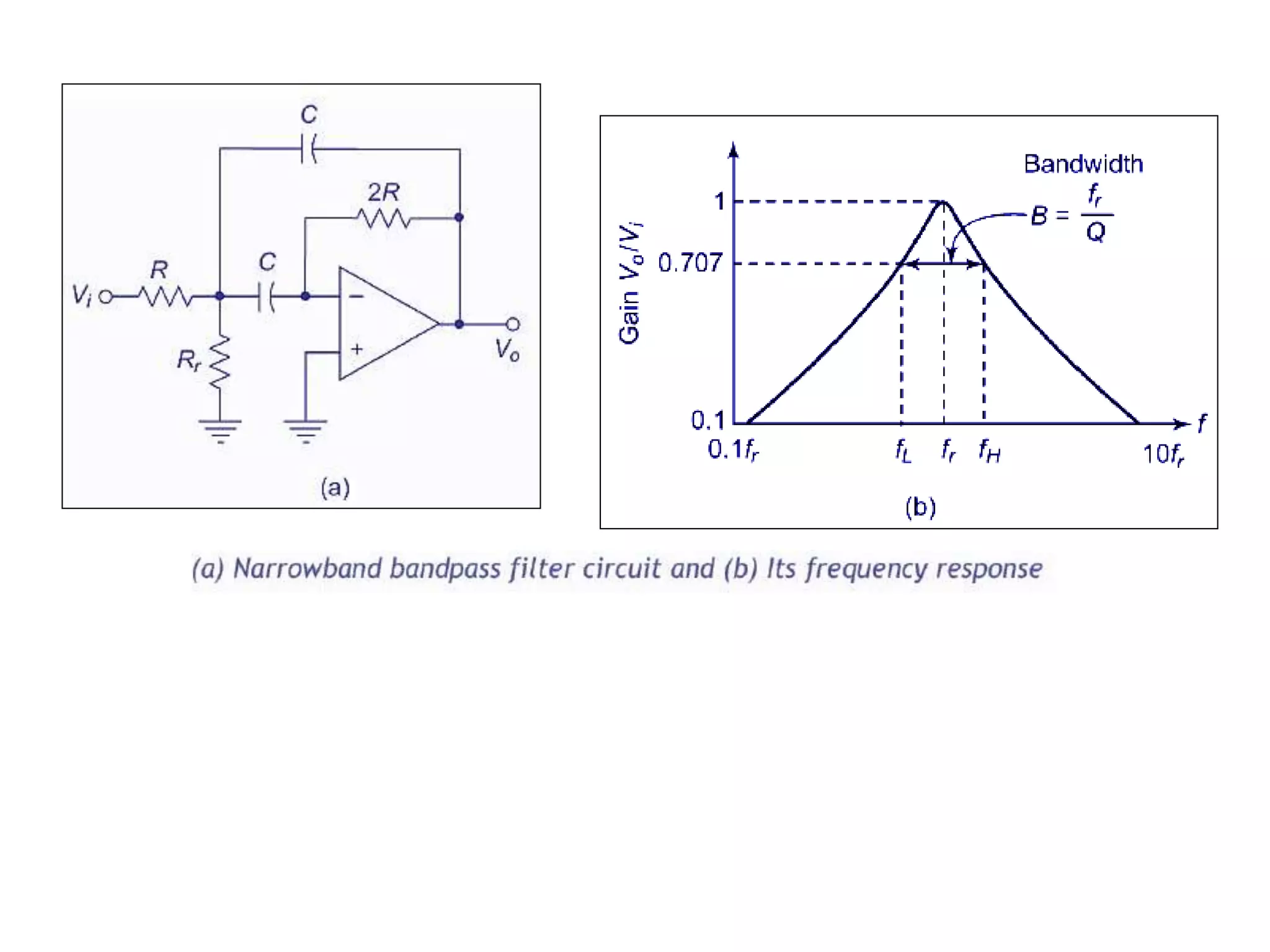
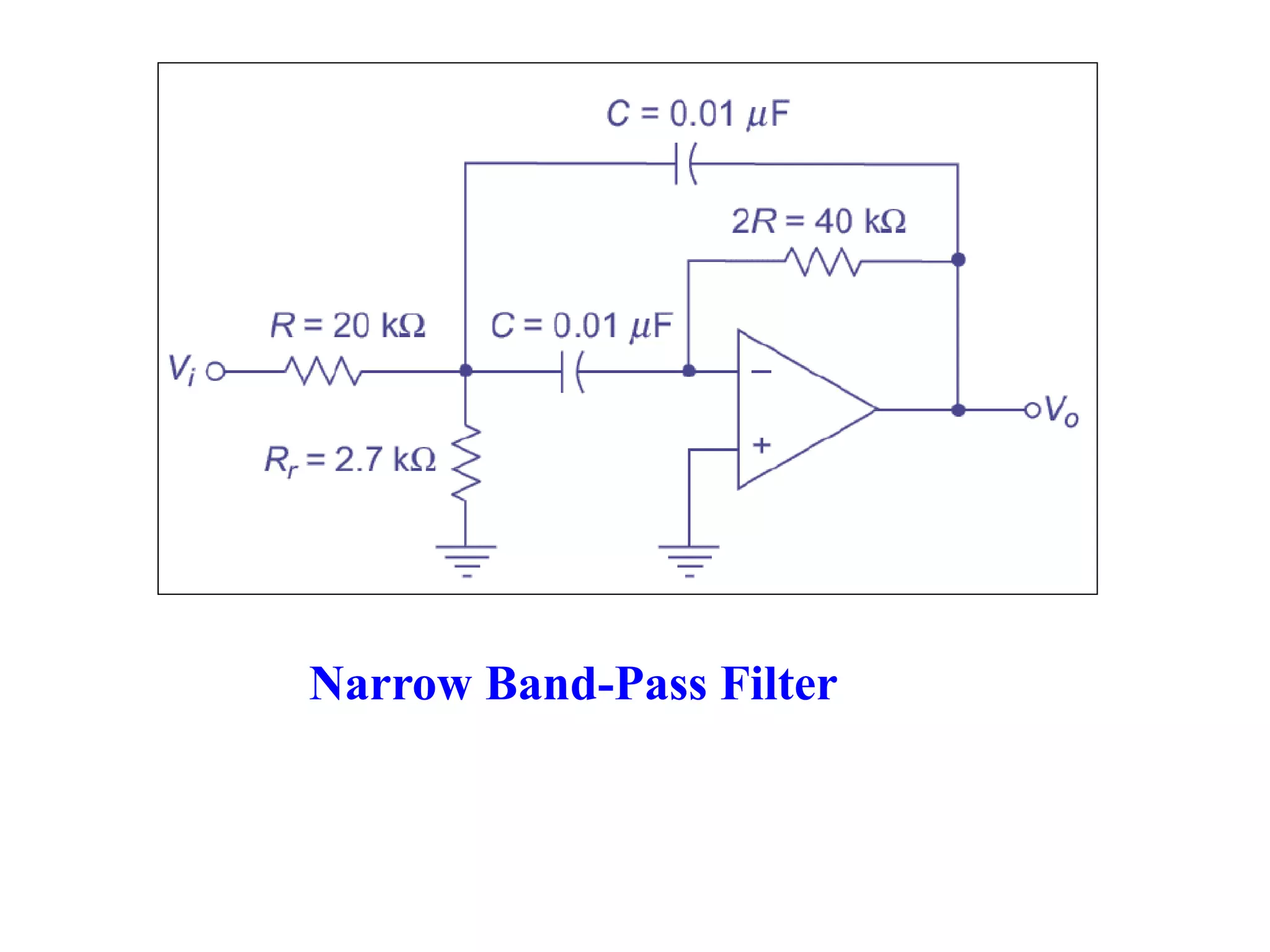
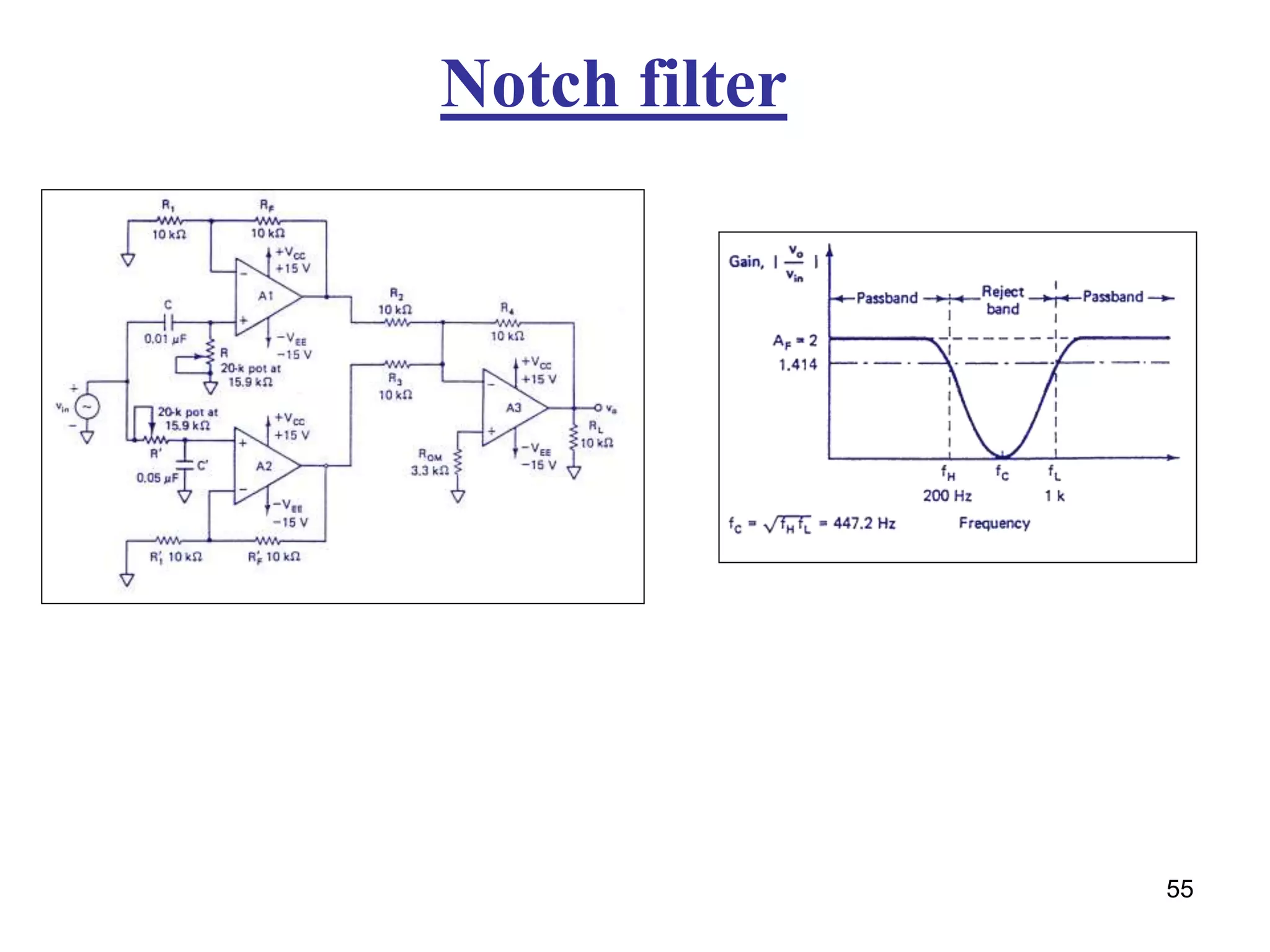
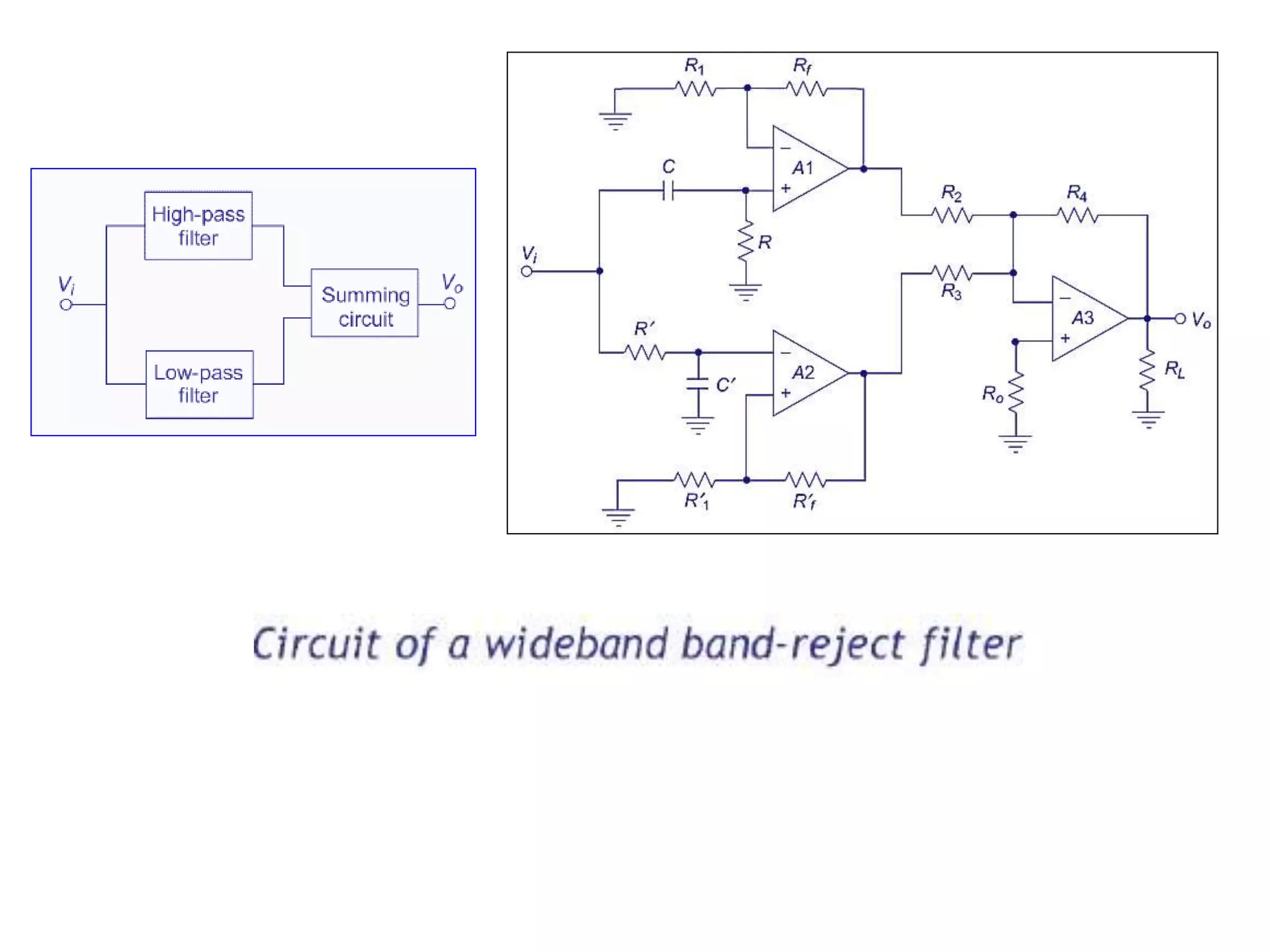
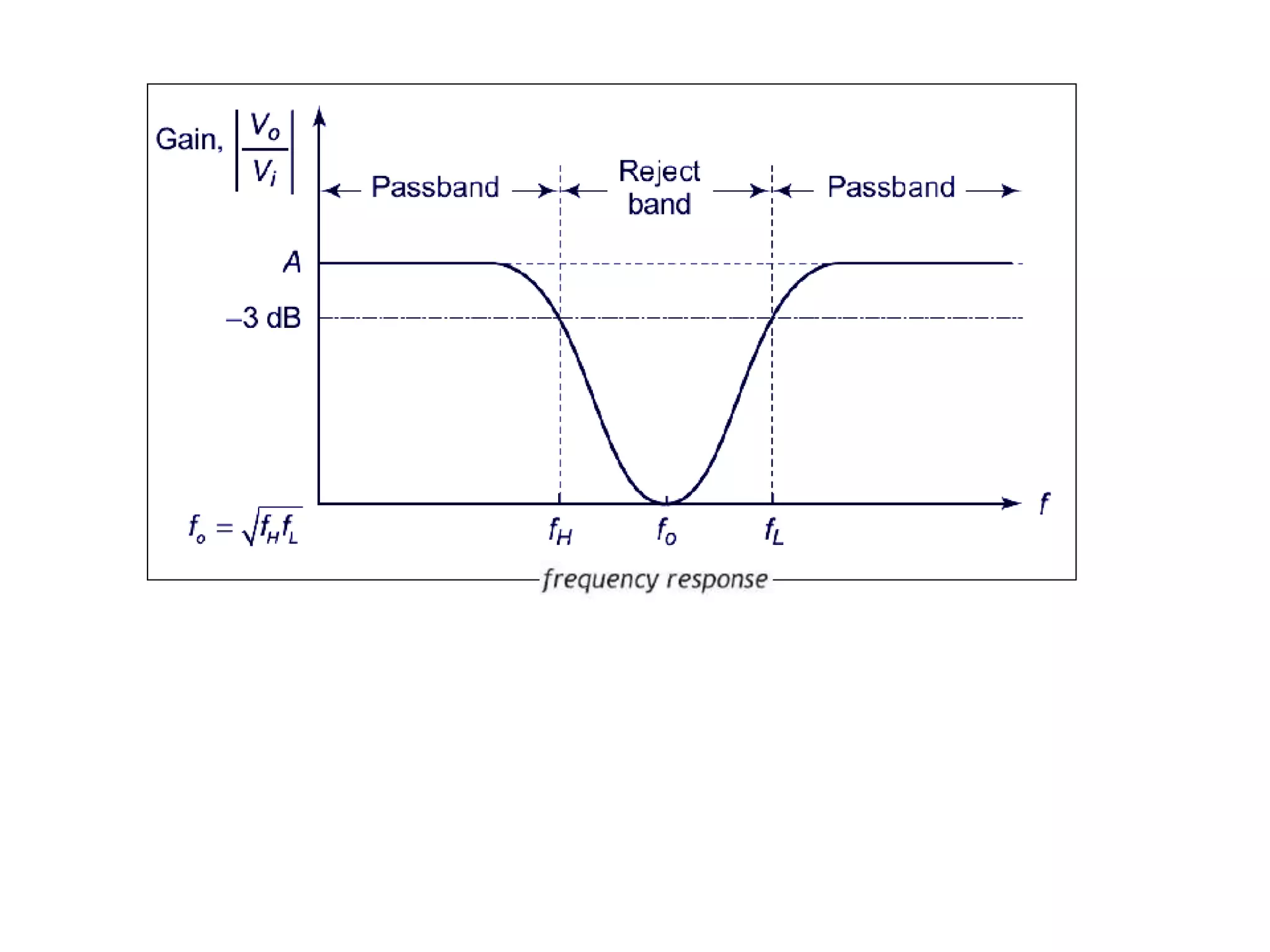
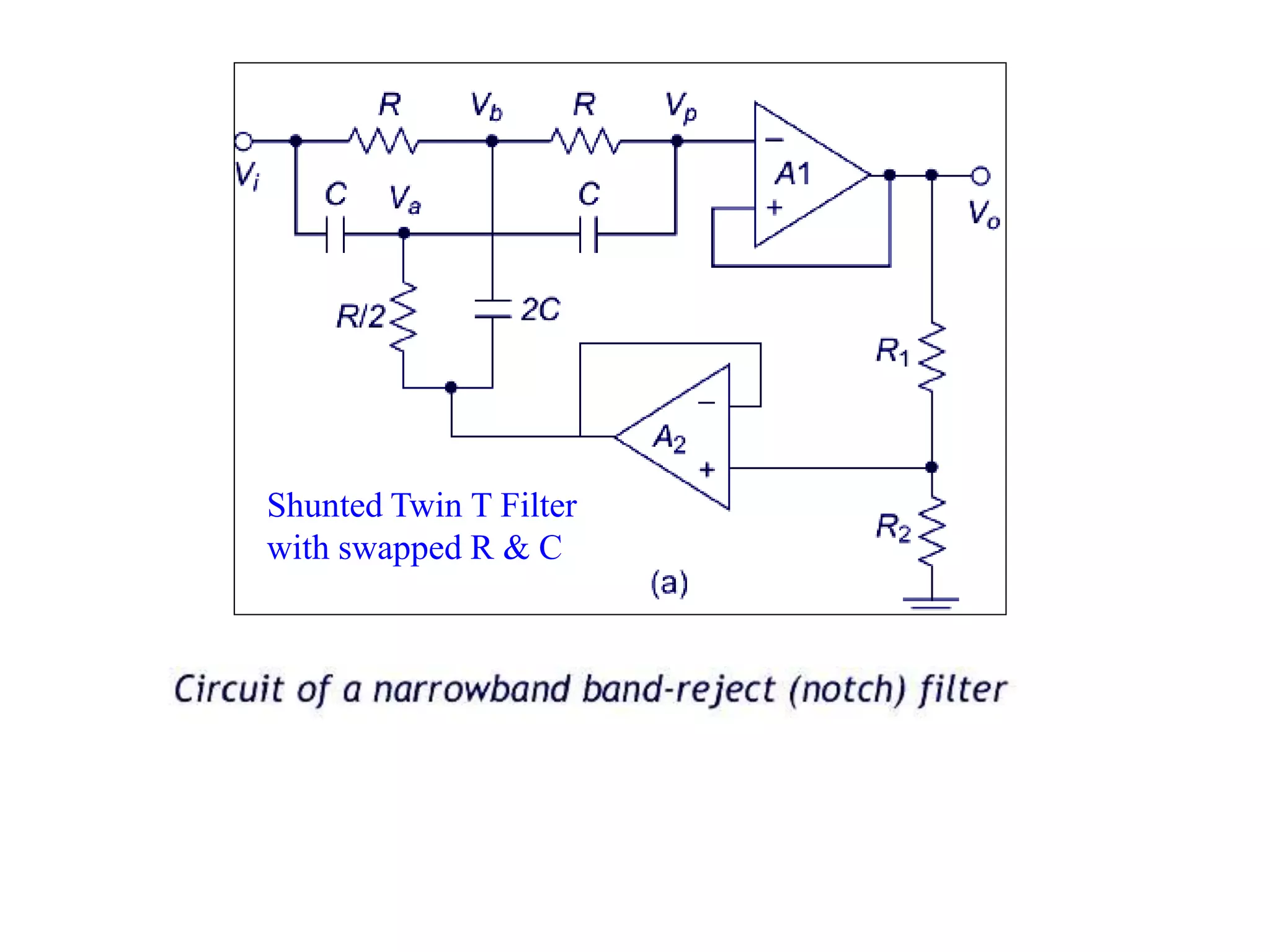
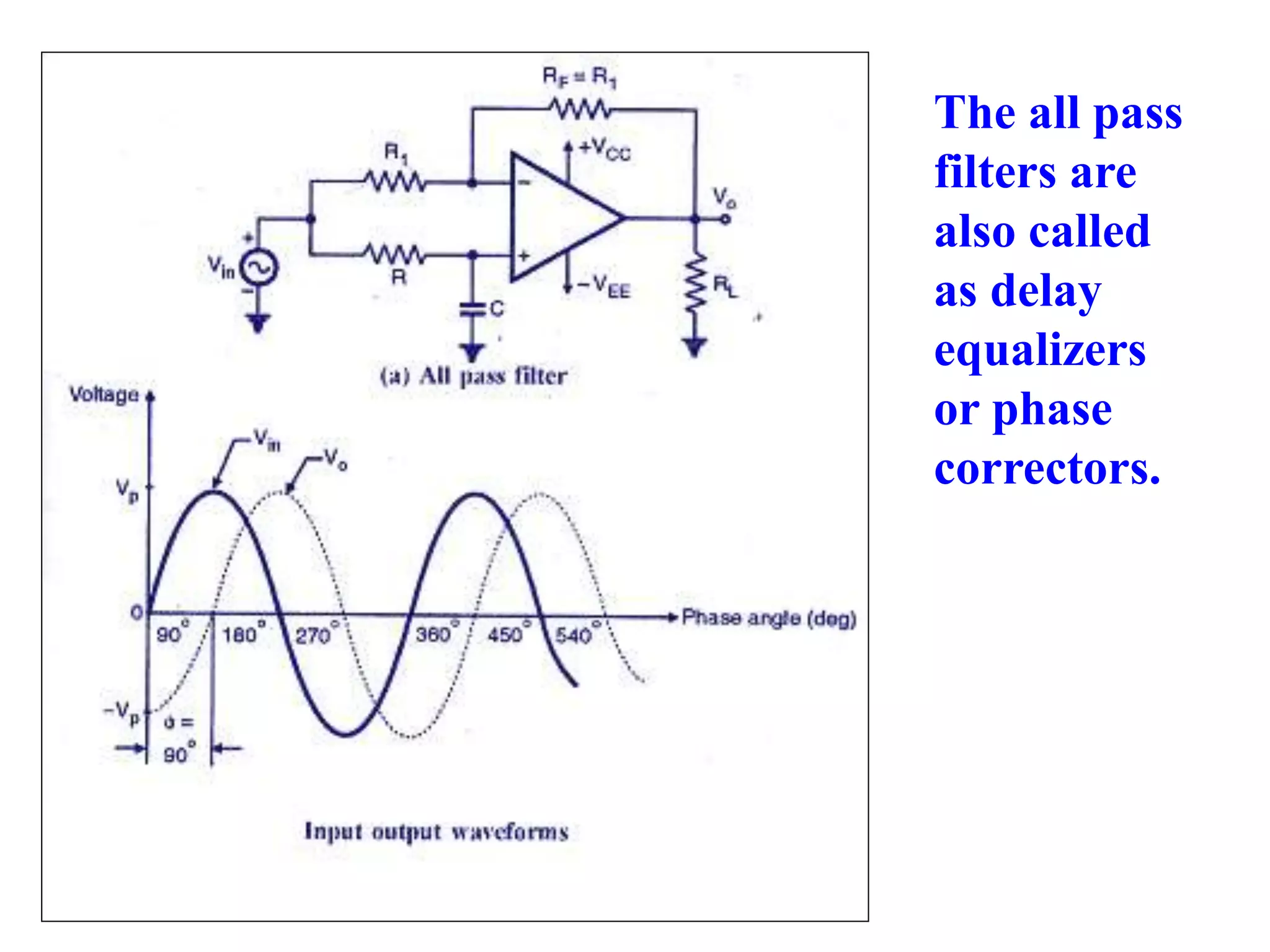
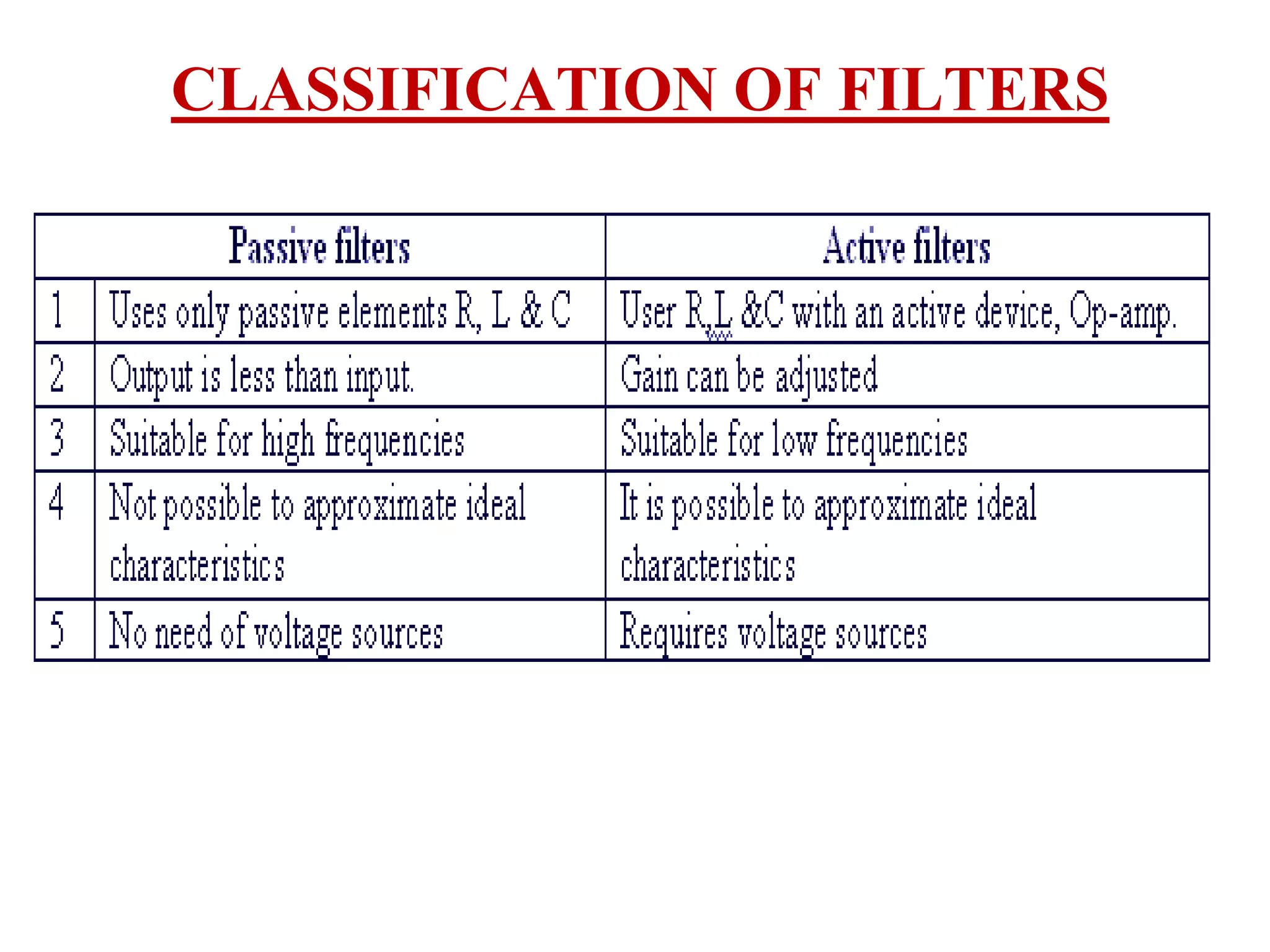
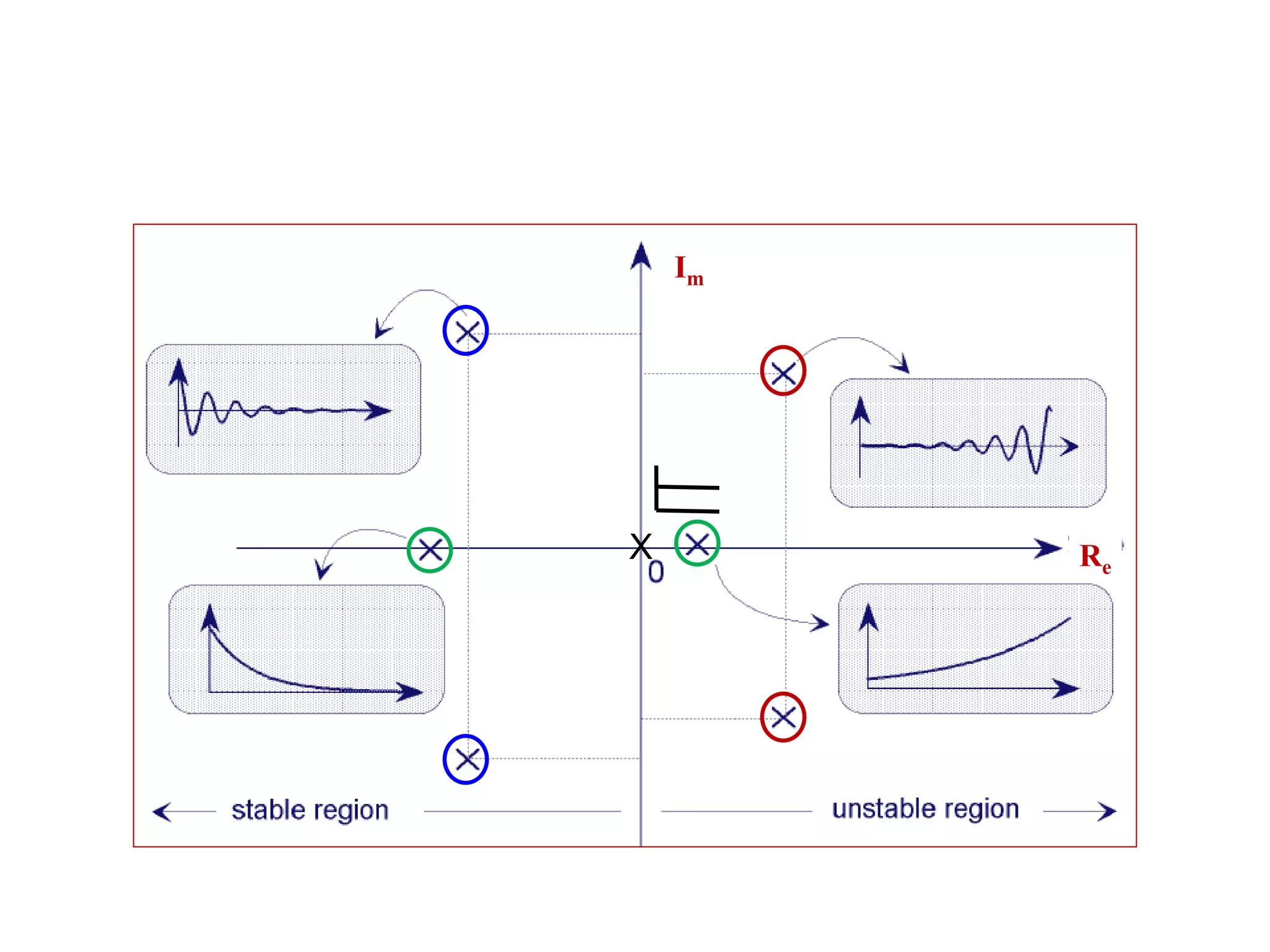
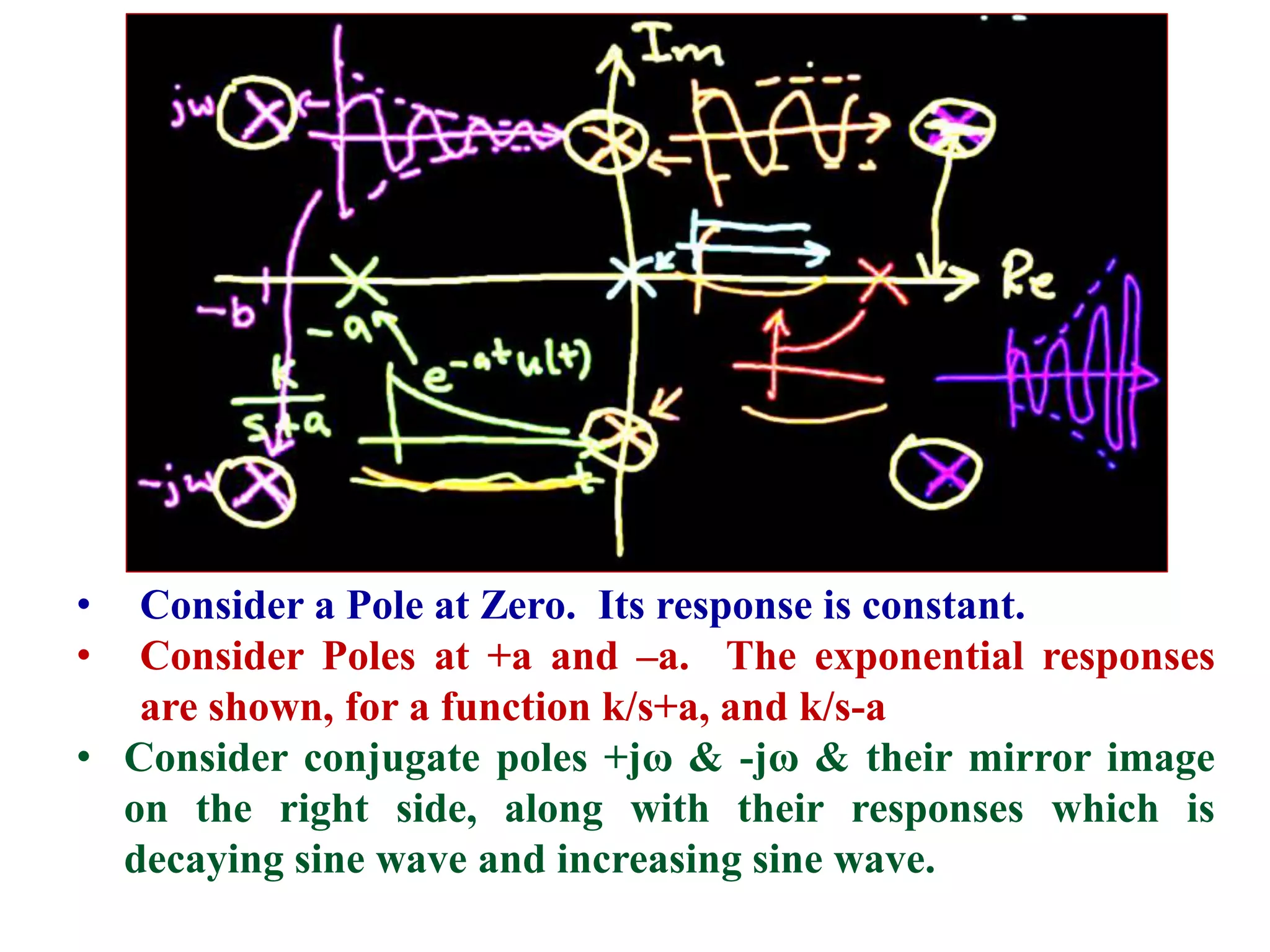
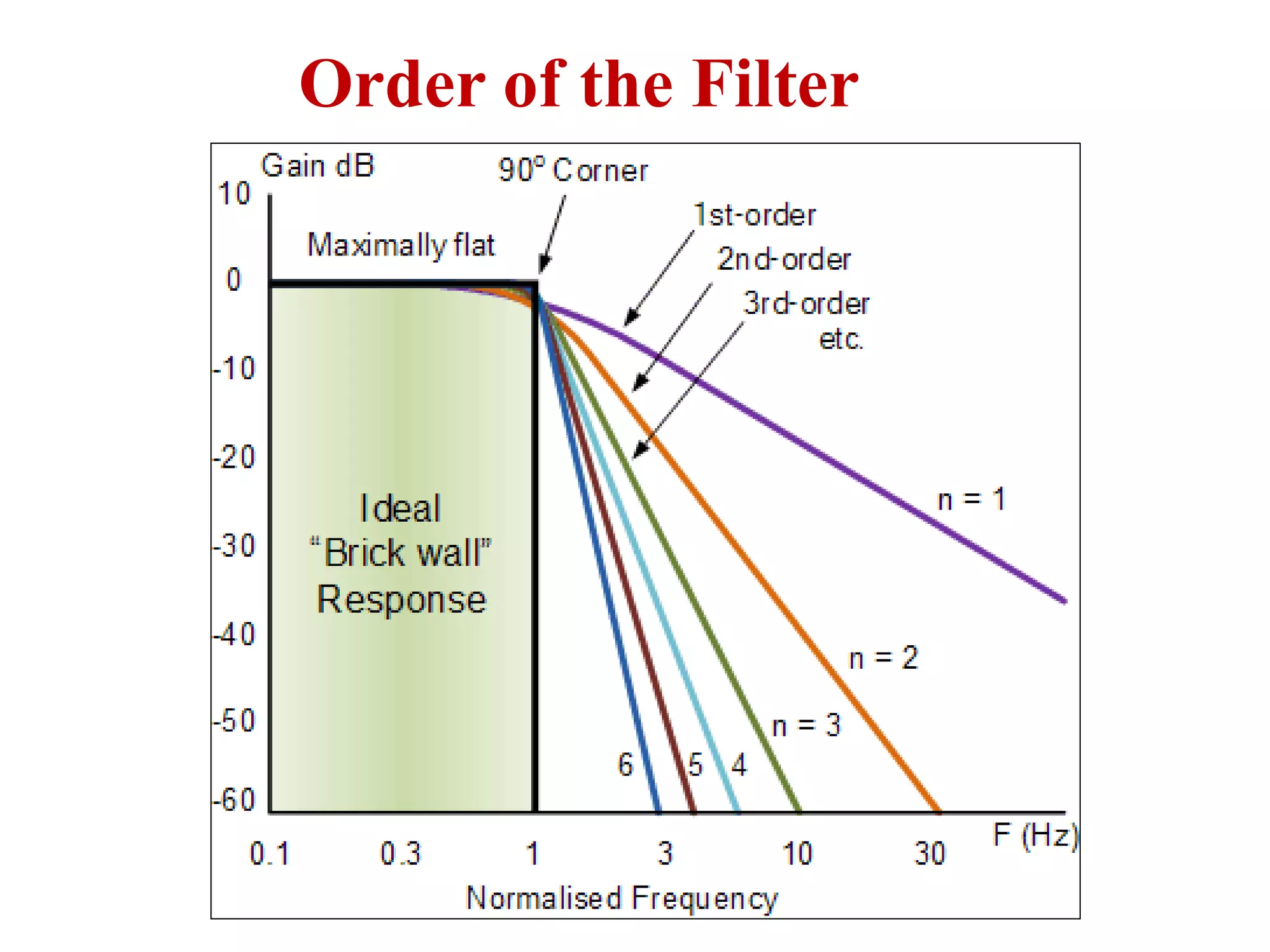
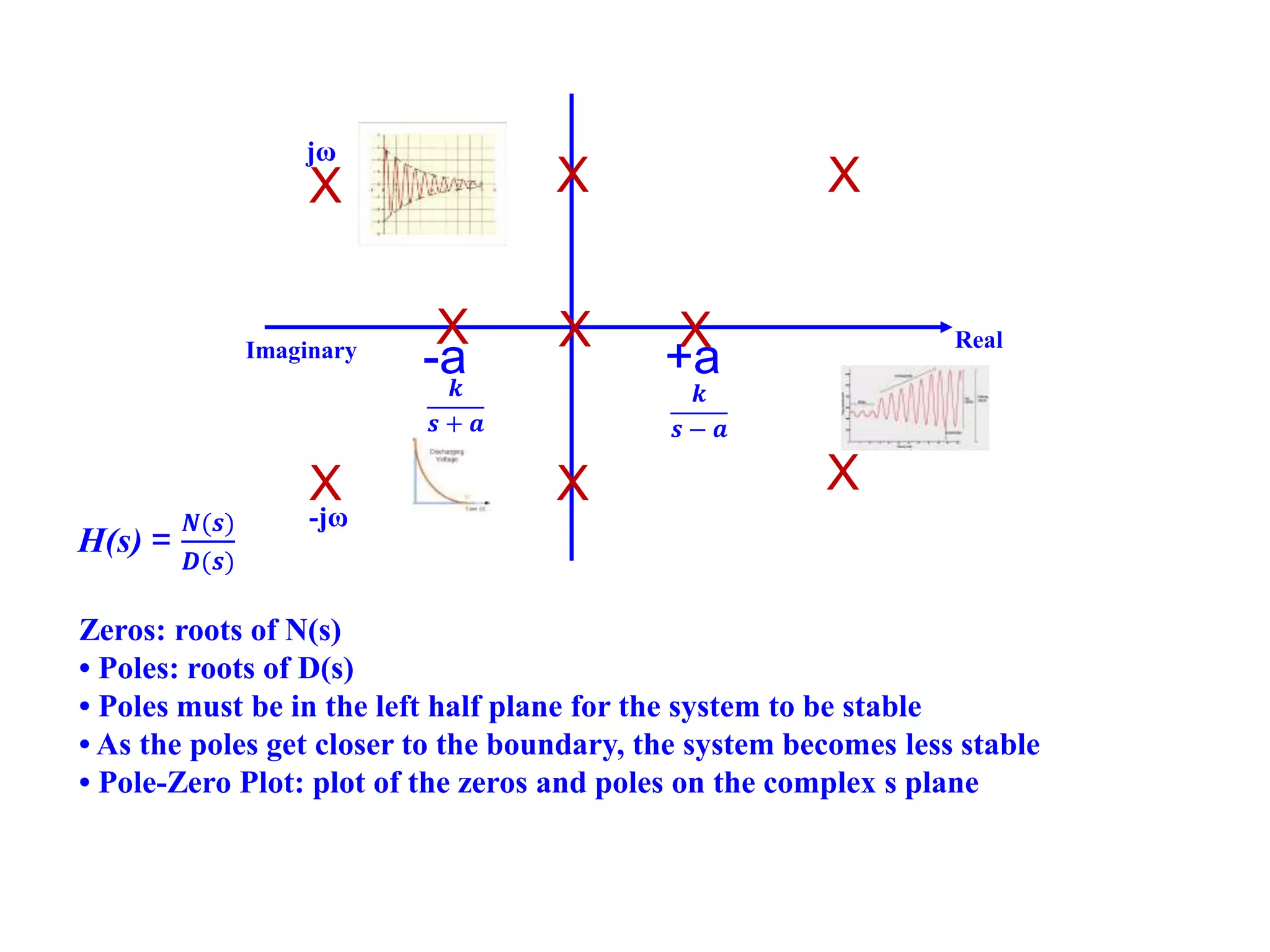
This document discusses active filters and provides information on different types of filters including: - Butterworth, Chebyshev, and Cauer filters and their magnitude responses. - Classification of filters as low pass, high pass, band pass and band reject based on their frequency responses. - Advantages of active filters over passive filters such as greater gain and flexibility in design. - Key concepts such as poles, zeros and order of filters and how they determine the frequency response. 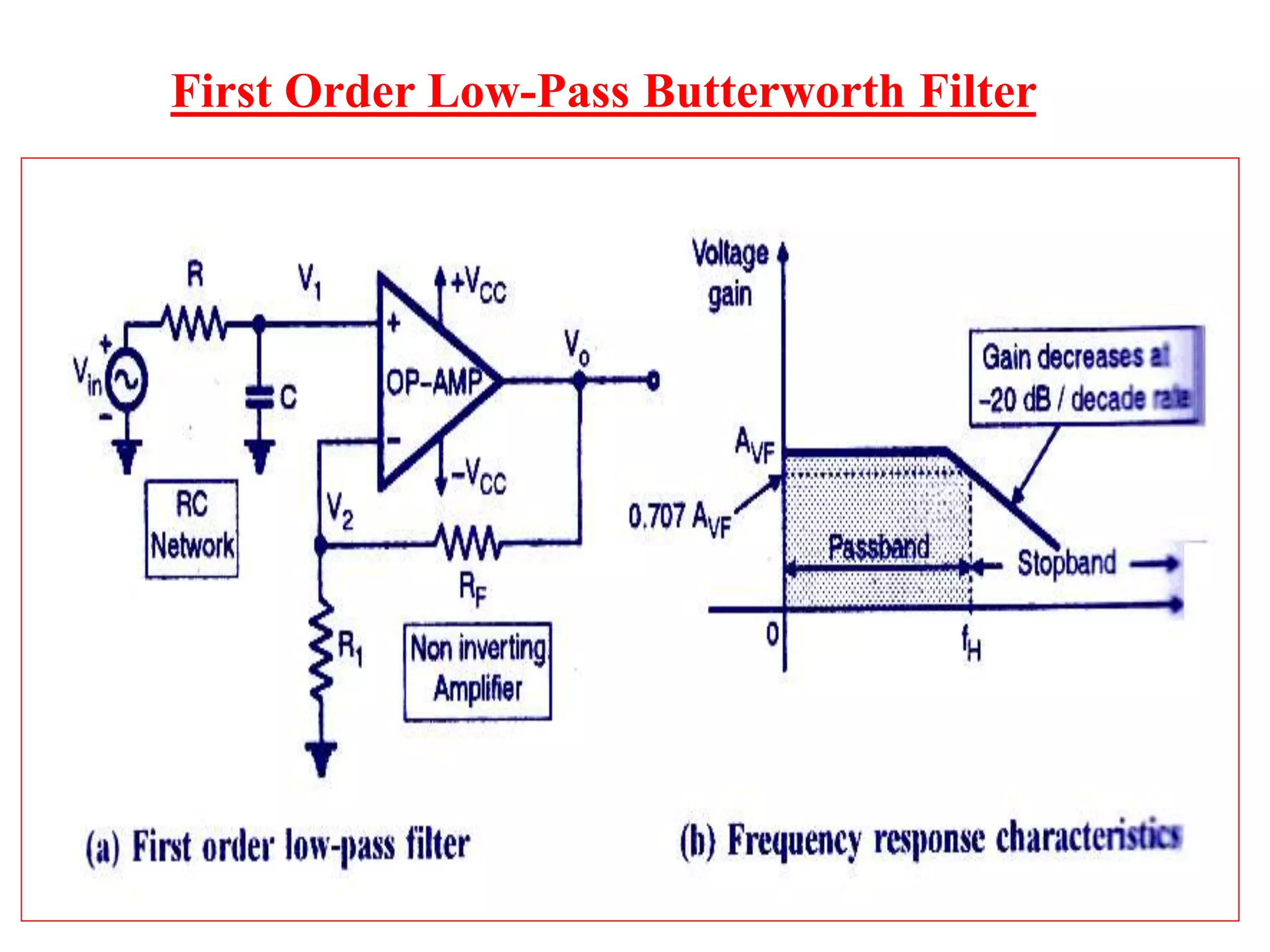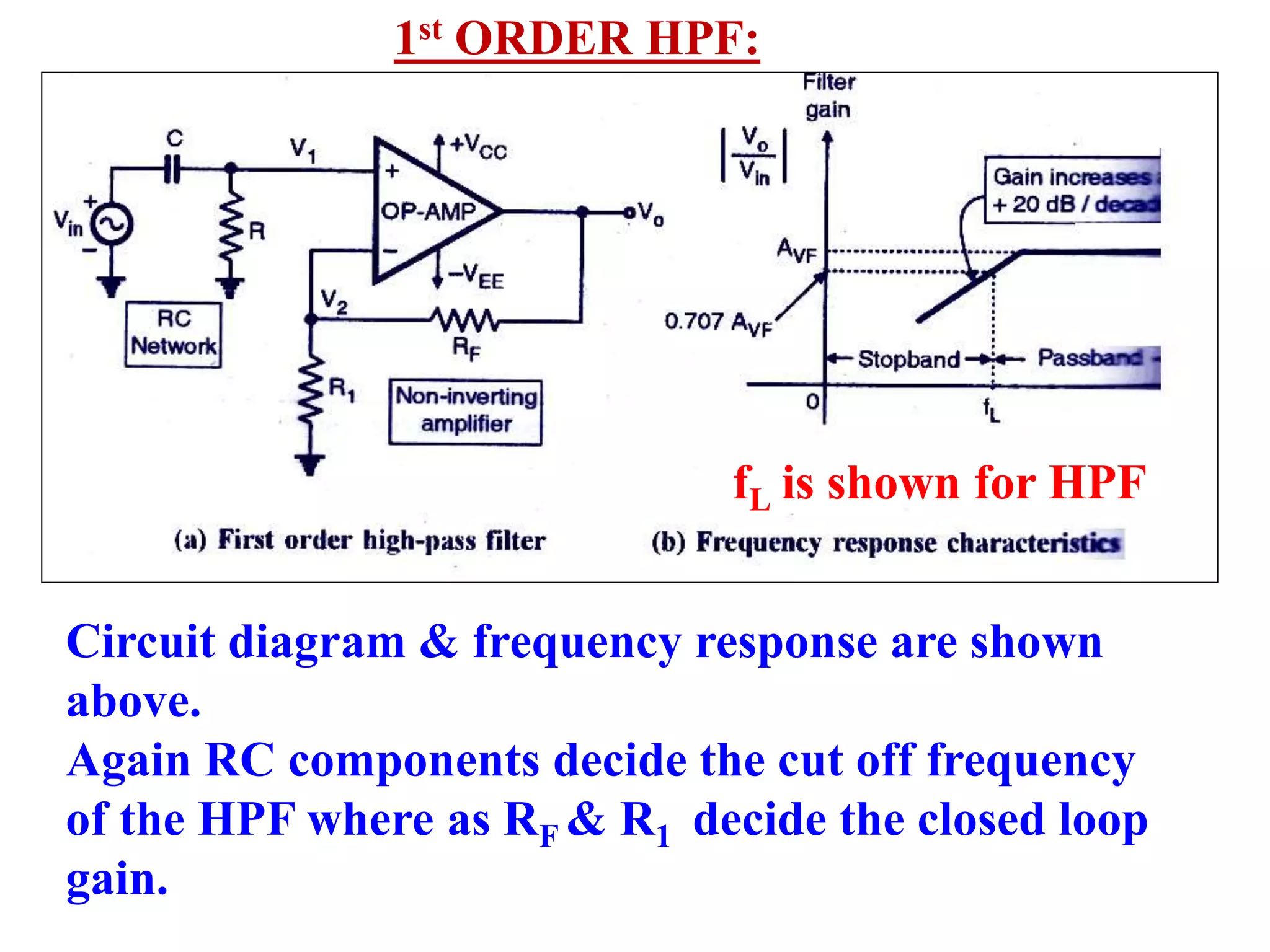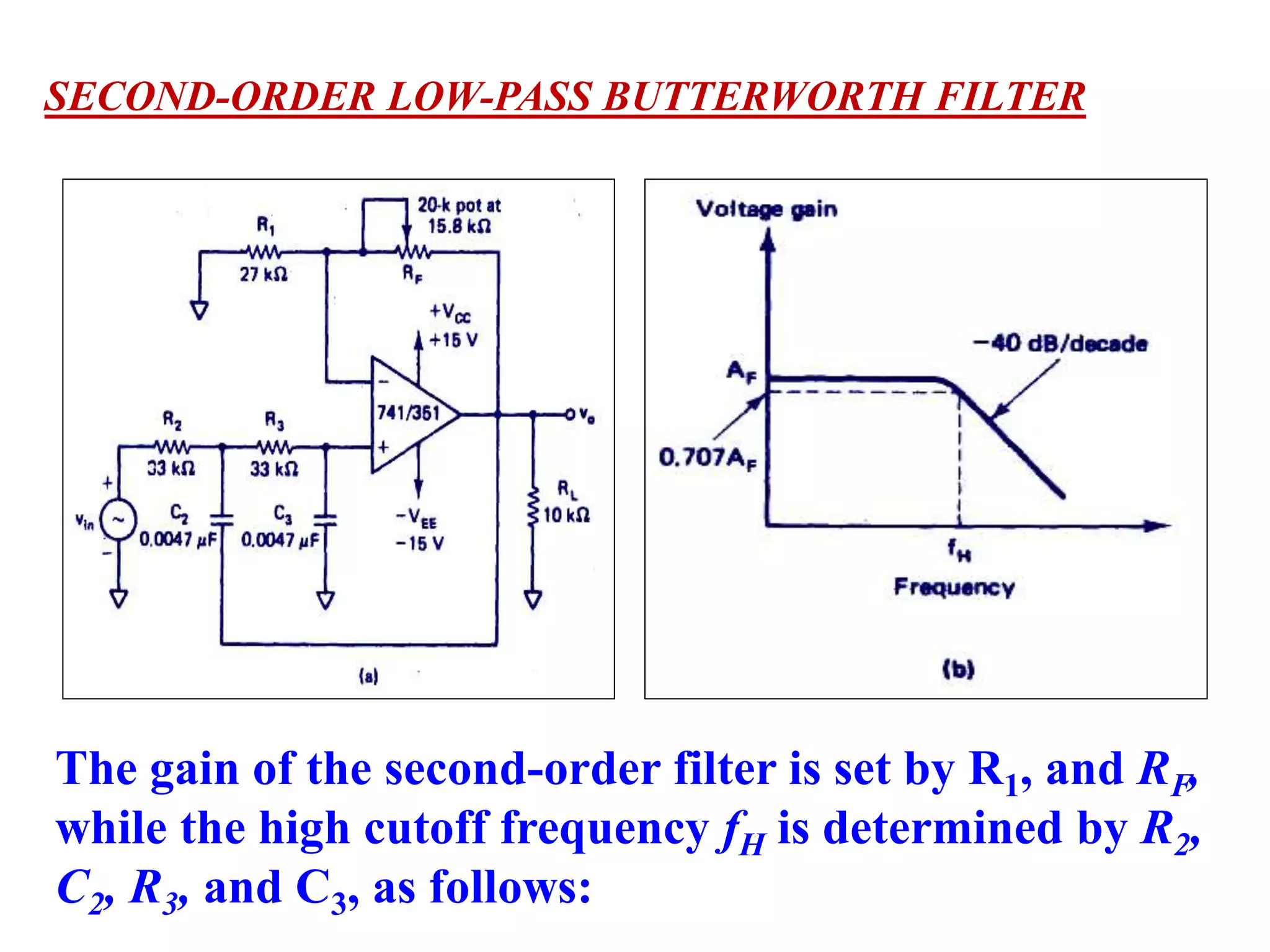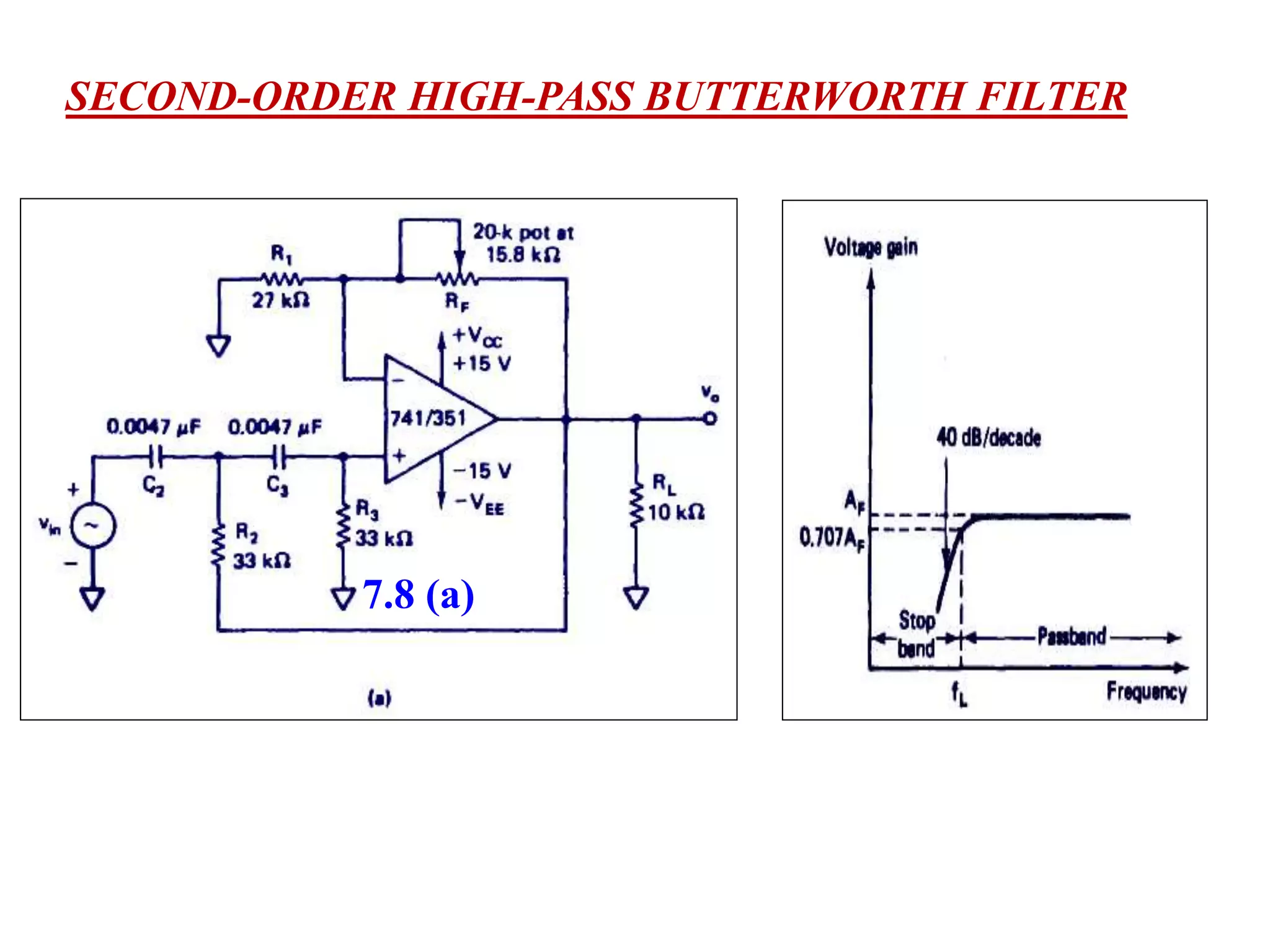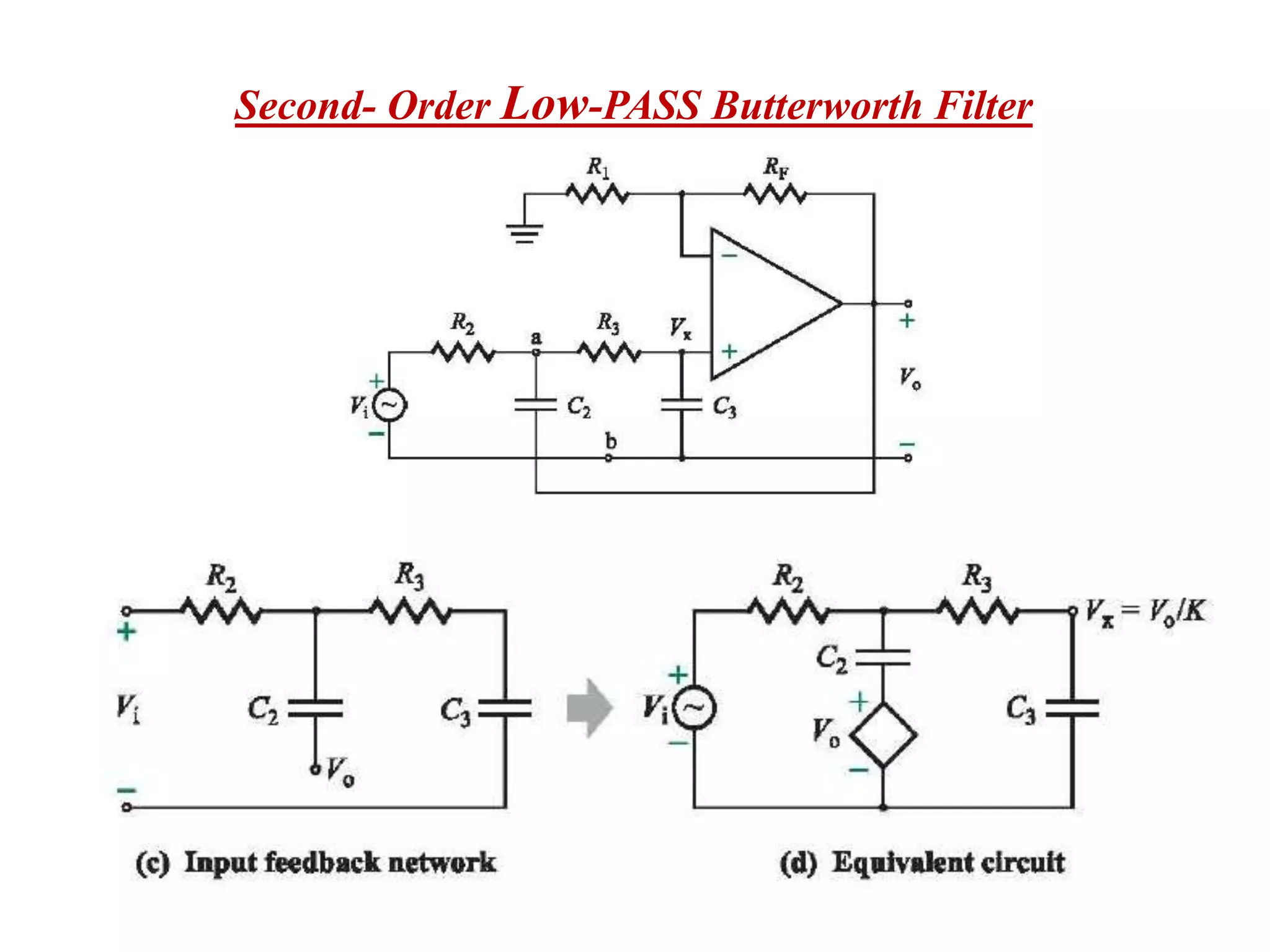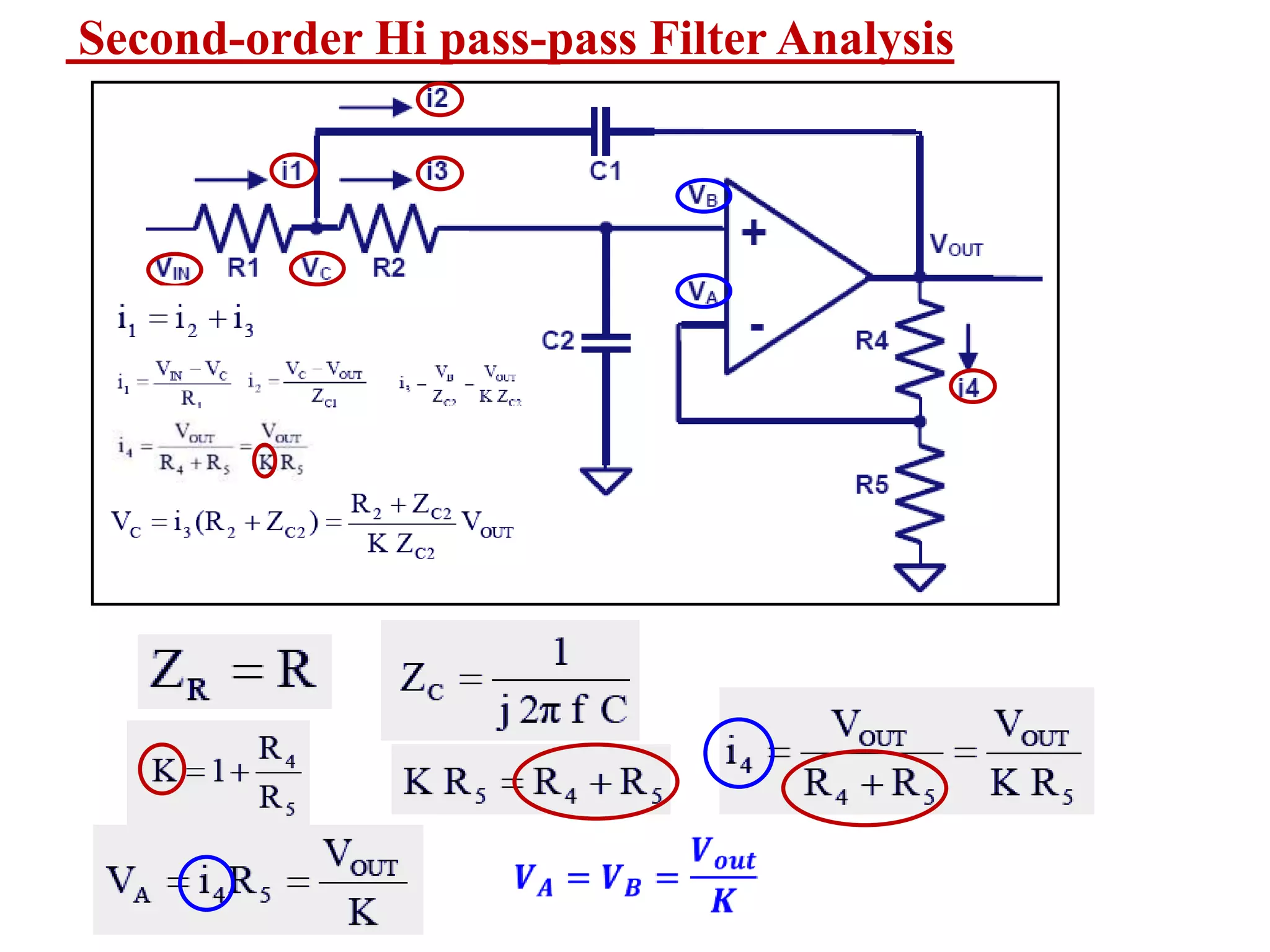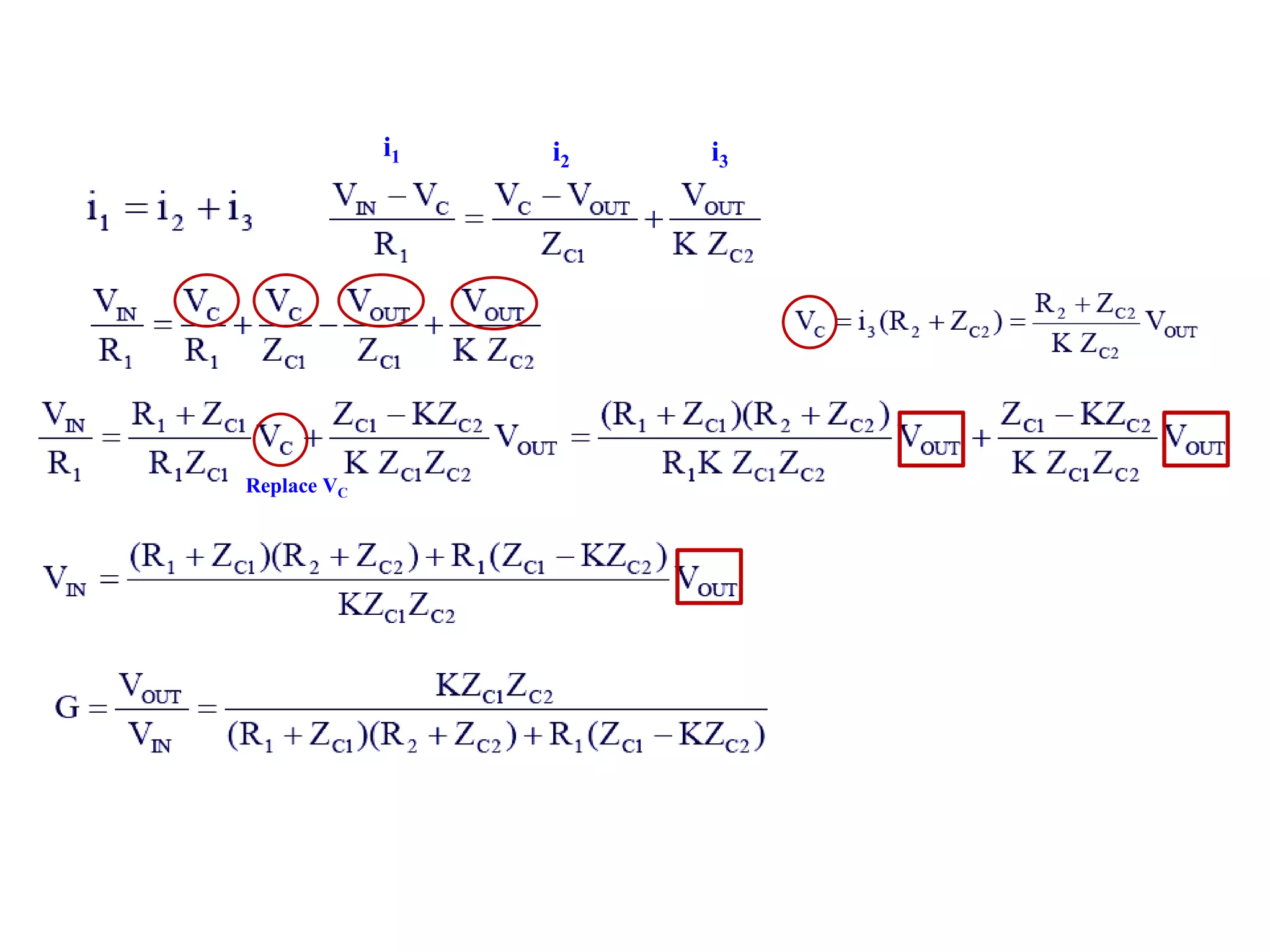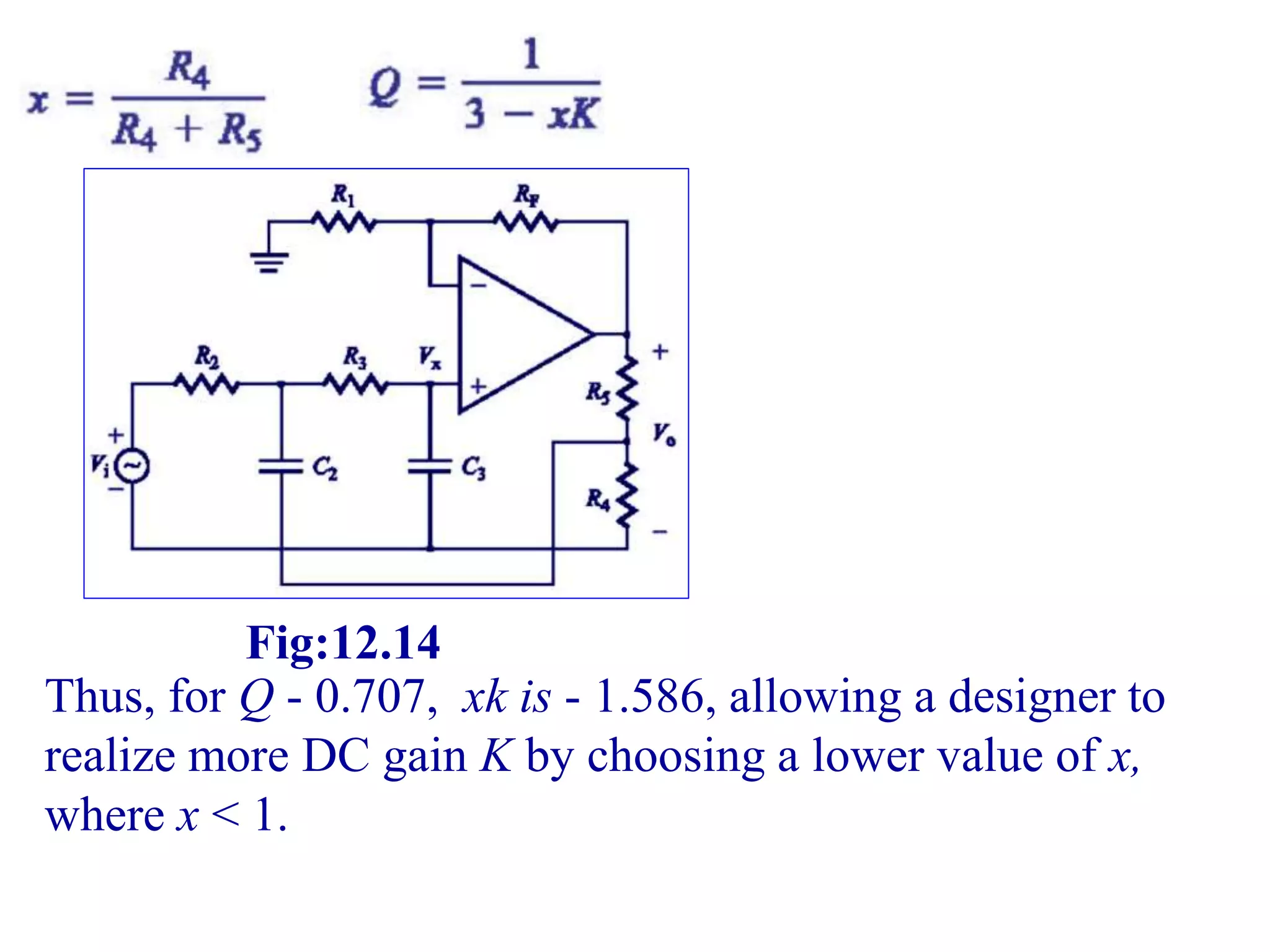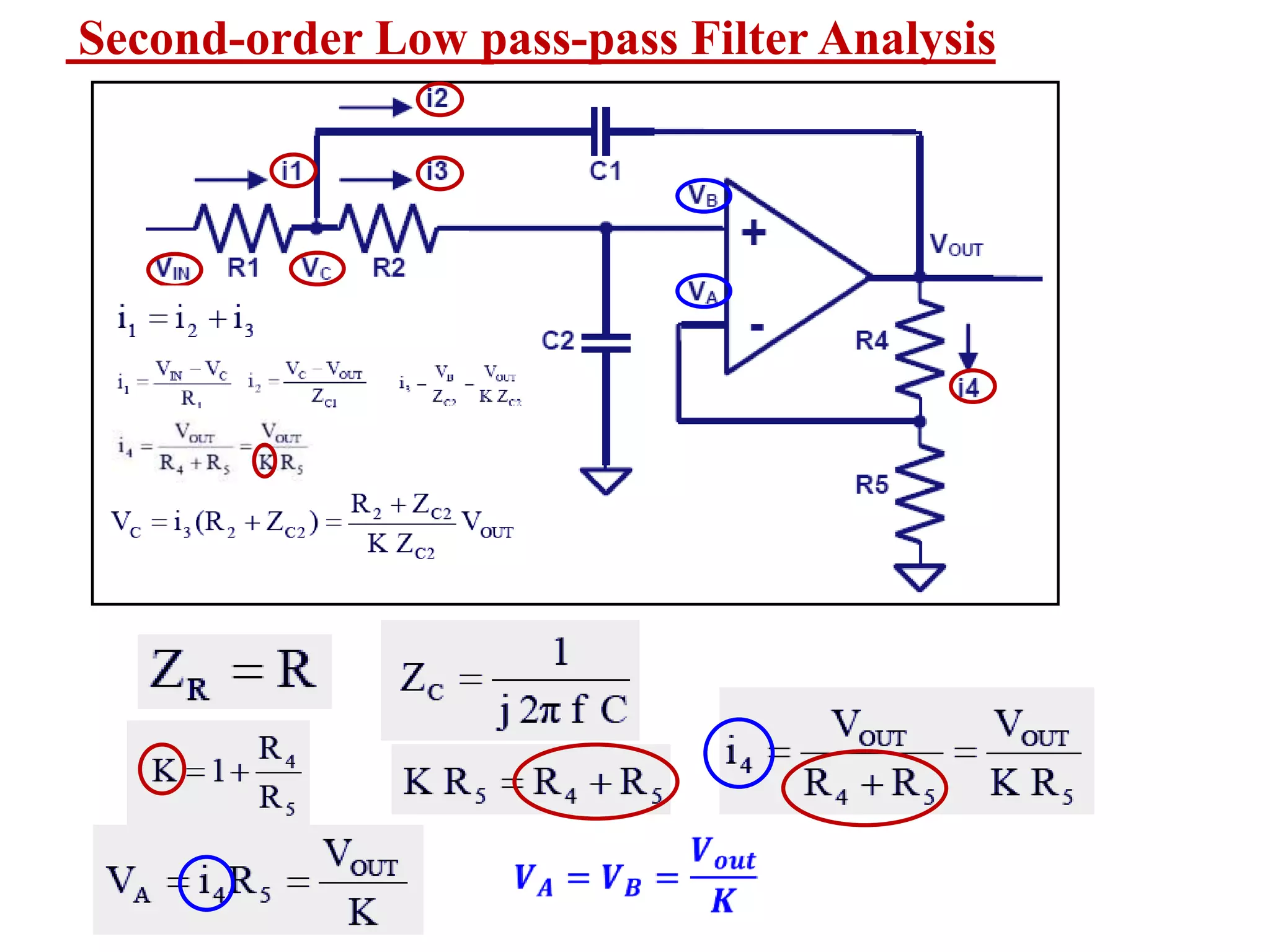- Design procedures for first and second order low pass Butterworth filters using op-amps.

1. Active Filters
Introduction, Active versus Passive Filters,
Types of Active Filters, First-Order Filters,
The Biquadratic Function, Butterworth
Filters, Transfer Function Realizations, Low
pass Filters, High-Pass Filters, Band-Pass
Filters, Band-Reject Filters, All-Pass Filters,
Switched Capacitor Filters, Filter Design
Guide Lines.
Syllabus

2. Filter Basics
• A filter is a frequency-selective circuit that passes
a specified band of frequencies and blocks or
attenuates signals of frequencies outside this band.
• A filter is used to remove (or attenuate) unwanted
frequencies in an audio signal
• “Stop Band” – the part of the frequency spectrum
that is attenuated by a filter.
• “Pass Band” – part of the frequency spectrum
that is unaffected by a filter.
• Filters are usually described in terms of their
“frequency responses,” e.g. low pass, high pass,
band pass, band reject (or notch)

3. Advantages of Active Filters over Passive Filters
(i) The maximum value of the transfer function or gain is greater
than unity.
(ii) The loading effect is minimal, which means that the output
response of the filter is essentially independent of the load
driven by the filter.
(iii) The active filters do not exhibit insertion loss. Hence, the
passband gain is equal to 0 dB.
(iv) Complex filters can be realized without the use of inductors.
(v) The passive filters using R, L and C components are
realizable only for radio frequencies. Because, the inductors
become very large, bulky and expensive at audio
frequencies. Due to low Q at low frequency applications,
high power dissipation is incurred. The active filters
overcome these problems.

4. (vi) Rapid, stable and economical design of filters for variety of
applications is possible.
(vii) The active filters are easily tunable due to flexibility in gain
and frequency adjustments.
(viii) The op-amp has high input impedance and low output
impedance. Hence, the active filters using op-amp do not
cause loading effect on the source and load. Therefore,
cascading of networks does not need buffer amplifier.
(ix) Active filters for fixed frequency and variable frequency can
be designed easily. The adjustable frequency response is
obtained by varying an external voltage signal.
(x) There is no restriction in realizing rational function using
active networks.
(xi) Use of active elements eliminates the two fundamental
restrictions of passivity and reciprocity of RLC networks.

5. Limitations of Active Filters over Passive Filters
(i) The high frequency response is limited by the gain-
bandwidth product and slew rate of the practical
op-amps, leading to comparatively lower
bandwidth than the designed bandwidth.
(ii) The design of active filters becomes costly for high
frequencies.
(iii) Active filters require dual polarity dc power
supply whereas passive filters do not.
(iv) The active element is prone to the process
parameter variations and they are sensitive to
ambient conditions like temperature. Hence, the
performance of the active filter deviates from the
ideal response.

6. Ideal Filter Characteristics
Filter Characteristics

7. CLASSIFICATION OF FILTERS

8. 8
Types of Filters
• Butterworth – Flat response in the pass
band & stop band and called flat-flat filter.
• Chebyshev – steeper roll-off but exhibits
pass band ripple (making it unsuitable for
audio systems) & flat stopband.
• Cauer – It has equiripple both in pass &
stop band.

9. Butterworth filter
magnitude response
Chebyshev filter
magnitude response
Cauer filter magnitude response
passband
stopband
passband
passband
stopband
stopband

10. FILTERS BASED ON FREQUENCY
Low pass filter (LPF) High pass filter (LPF)
20db/decade
20db/decade

11. Understanding Poles and Zeros
The transfer function provides a basis for determining
important system response characteristics
The transfer function is a rational
function in the complex variable s = σ + jω, that is
zi’s are the roots of the equation N(s) = 0, and are defined to be
the system zeros, and the pi’s are the roots of the equation
D(s) = 0, and are defined to be the system poles.
N(s) = 0; Zeros. D(s) = 0; Poles.

12. Example
A linear system is described by the differential equation
Find the system poles and zeros. Solution: From the
differential equation the transfer function is
Zero at -1/2
Poles at -2 & -3

13. X Re
Im

14. • Consider a Pole at Zero. Its response is constant.
• Consider Poles at +a and –a. The exponential responses
are shown, for a function k/s+a, and k/s-a
• Consider conjugate poles +jω & -jω & their mirror image
on the right side, along with their responses which is
decaying sine wave and increasing sine wave.

15. The equation shown has 3 poles & one Zero at -1.
Zeros show how fast the amplitudes vary.

16. Frequency Response of filters
• Ideal
• Practical
• Filters are often described in terms of poles and
zeros
– A pole is a peak produced in the output spectrum
– A zero is a valley (not really zero)

17. Order of the Filter

18. Comparison of FIR & IIR Filter
1. FIR (Finite Impulse Response) (non-
recursive) filters produce zeros.
2. In signal processing, a finite impulse response
(FIR) filter is a filter whose impulse response (or
response to any finite length input) is
of finite duration, because it settles to zero in finite
time.
3. Filters combining both past inputs and past outputs
can produce both poles and zeros.
4. FIR filters can be discrete- time or continuous-time,
and digital or analog.
5. FIR filters are dependent upon linear-phase
characteristics.
6. FIR is always stable
7. FIR has no limited cycles.
8. FIR has no analog history.
9. FIR is dependent upon i/p only.
10. FIR’s delay characteristics is much better, but
they require more memory.
11. FIR filters are used for tapping of a higher-
order.
1. IIR (infinite Impulse Response) (recursive)
filters produce poles.
2. This is in contrast to infinite impulse response (IIR)
filters, which may have internal feedback and may
continue to respond indefinitely (usually decaying).
3. IIR filters are difficult to control and have no
particular phase.
4. IIR is derived from analog.
5. IIR filters are used for applications which are not
linear.
6. IIR can be unstable
7. IIR filters make polyphase implementation possible.
8. IIR filters can become difficult to implement, and also
delay and distortion adjustments can alter the poles
& zeroes, which make the filters unstable.
9. IIR filters are dependent on both i/p and o/p.
10. IIR filters consist of zeros and poles, and require less
memory than FIR filters.
11. IIR filters are better for tapping of lower-orders, since
IIR filters may become unstable with tapping higher-
orders.

19. ACTIVE FILTERS USING OP-AMP:
Filters are frequency selective circuits. They are required to pass
a specific band of frequencies and attenuate frequencies outside
the band. Filters using an active device like OPAMP are called
active filters. Other way to design filters is using passive
components like resistor, capacitor and inductor.
ADVANTAGES OF ACTIVE FILTERS:
Possible to incorporate variable gain
Due to high Zi & Z0 of the OPAMP, active filters do not load the
input source or load.
Flexible design.

20. FREQUENCY RESPONSE OF FILTERS:
Gain of a filter is given as, G=Vo/Vin
Ideal & practical frequency responses of different types of
filters are shown below.

21. First Order Low-Pass Butterworth Filter

22. Because of simplicity, Butterworth filters are considered.
• In 1st. order LPF which is also known as one pole
LPF. Butterworth filter and it’s frequency response
are shown above.
• RC values decide the cut-off frequency of the filter.
• Resistors R1 & RF will decide it’s gain in pass band.
As the OP-AMP is used in the non-inverting
configuration, the closed loop gain of the filter is given
by
1
1
R
R
A F
VF 

23. )1(1 


 in
C
C
V
jXR
jX
V
fC
XC
2
1

)2(
2
12
2
1
2
1
1 




















j
fRC
V
jfRC
jV
fC
jR
V
fC
j
V inin
in



 fRCj
Vin
21
EXPRESSION FOR THE GAIN OF THE
FILTER:
Reactance of the capacitor is,
Equation (1) becomes
Voltage across the capacitor
V1 =

24. f = frequency of the input signal
















H
VF
in
inF
VF
f
f
j
A
V
V
fRCj
V
R
R
VAV
1
21
1
0
1
10

Output of the filter is,

25. The operation of the low-pass filter can be verified from
the gain magnitude equation, (7-2a):
1. At very low frequencies, that is, f < fH,
2. At f = fH,
3. f > fH,

26. DESIGN PROCEDURE:
Step1: Choose the cut-off frequency fH
Step2: Select a value of ‘C’ ≤ 1µF (Approximately
between .001 & 0.1µF)
Step3: Calculate the value of R using
Step4: Select resistors R1 & R2 depending on the desired
pass band gain.
=2. So RF=R1

27. For a first order Butterworth LPF, calculate the cut –off
frequency if R=10K & C=0.001µF.Also calculate the
pass band voltage gain if R1=10K RF =100K
KHz
RC
fH 915.15
10001.010102
1
2
1
63


 

Design a I order LPF for the following specification
Pass band voltage gain = 2. Cut off frequency, fC = 10KHz.
AVF = 2; Let RF = 10K
1+100K/10K =11
RF/R1=1 Let C = 0.001µF
63
10001.010102
1
2
1
&
2
1



 Cf
R
RC
f
H
H
R=15.9K

28. Circuit diagram & frequency response are shown
above.
Again RC components decide the cut off frequency
of the HPF where as RF & R1 decide the closed loop
gain.
1st ORDER HPF:
fL is shown for HPF

29. fC
WhereX
V
jXR
R
V
C
in
C
2
1
1



 
inin V
fRCj
fCjR
fCj
R
R
V
fC
j
R
R
V



21
2
2
1
2
1






 in
l
L
V
f
f
j
f
f
j













1
in
L
L
VF
VF V
f
f
j
f
jf
A
VAV








1
. 10














L
L
VF
in
f
f
j
f
jf
A
V
V
1
0
EXPRESSION FOR THE GAIN:
Output voltage =
Gain =
Voltage
Magnitude=

30. SECOND-ORDER LOW-PASS BUTTERWORTH FILTER
The gain of the second-order filter is set by R1, and RF,
while the high cutoff frequency fH is determined by R2,
C2, R3, and C3, as follows:

31. High Cutoff frequency,
SECOND-ORDER LOW-PASS BUTTERWORTH FILTER
AF = 1.586 for 2nd order
Butterworth Filter

32. Filter Design
1. Choose a value for the high cutoff frequency fH
2. To simplify the design calculations, set R2 = R3 = R and
C2 = C3 = C. Then choose a value of C ≤ 1µF
3. Calculate the value of R using Equation for fH:
4. Finally, because of the equal resistor (R2 = R3) and
capacitor (C2 = C3) values, the pass band voltage gain AF
= (1 + RF/R1) of the second-order low-pass filter has to be
equal to 1.586. That is, RF = 0.586/R1 This gain is
necessary to guarantee Butterworth response. Hence
choose a value of R1 < 100 kΩ and calculate the value of
RF .

33. As in the case of the first-order filter, a second-order
high-pass filter can be formed from a second-order
low-pass filter simply by interchanging the
frequency determining resistors and capacitors.
Figure 7-8(a) shows the second-order high-pass
filter.
SECOND-ORDER HIGH-PASS BUTTERWORTH FILTER
𝒗 𝒐
𝒗𝒊𝒏
=
𝑨 𝑭
𝟏 +
𝒇 𝑳
𝒇
𝟒
AF = 1.586 for 2nd order
Butterworth Filter

34. 7.8 (a)
SECOND-ORDER HIGH-PASS BUTTERWORTH FILTER

35. Second- Order Low-PASS Butterworth Filter

36. Writing Kirchhoff's current law at node VA(S),
I1 = I1 + I2.
we have omitted S; for example Vin(S) is written as Vin.
Also, using the voltage-divider rule,
since RiF = ∞, IB = 0 A
Substituting the value of VA in Equation (C-7) and
solving for Vh we get
C-7

37. where AF = 1 + (RF/R1)-Therefore,
Solving this equation for V0/Vin, we have

38. For frequencies above fH, the gain of the second-order low-
pass filter rolls off at the rate of -40dB/decade. Therefore,
the denominator quadratic in the gain (V/Vin) equation must
have two real and equal roots. This means that

39. Second-order Hi pass-pass Filter Analysis

40. Replace VC
i1 i2 i3

41. Comparing the denominator of Eq. (12.50) with that of
Eq. (12.46) shows that Q can be related to K by

42. The frequency response of a second-order system at the 3-
dB point will depend on the damping factor ζ such that Q
= 1/ 2ζ (zeta). A Q-value of ( = 0.707), which represents
a compromise between the peak magnitude and the
bandwidth, causes the filter to exhibit the characteristics of
a flat passband as well as a stop band, and gives a fixed
DC gain of K = 1.586:
𝟏
𝟐
However, more gain can be realized by adding a voltage-
divider network. as shown in Fig. 12.14, so that only a
fraction x of the output voltage is fed back through the
capacitor C2 that is,

43. Thus, for Q - 0.707, xk is - 1.586, allowing a designer to
realize more DC gain K by choosing a lower value of x,
where x < 1.
Fig:12.14

44. Example:12:3
Solution
To simplify the design calculations, let R1 = R2 = R3 =R4
= R and let C2 = C3 = C. Choose a value of C less than or
equal to 1 µF. Let C = 0.01 µF. For R2 = R3 = R and C2 =
C3 = C, Eq. (12.49) is reduced to
RF = (K - 1)R1 = (4 - 1) = x = 15,916 = 47,748

46. Second-order Low pass-pass Filter Analysis

47. Replace VC
i1 i2 i3

48. Second-Order High-Pass Filters
The transfer function can be derived by applying the RC-
to-CR transformation and substituting 1/s for s in Eq.
(12.47). For R1 = R2 = R3 = R, and C2 = C3 = C, the
transfer function becomes

49. Example:12:6
For Q=1; Rs = R = 15,9160

53. Narrow Band-Pass Filter

54. DESIGN EQUATIONS:
Select C1 = C2 =C
FCCAf
Q
R
2
1 
 FC AQCf
Q
R

 22
22 Cf
Q
R
C
B


A is the gain at f =fC
1
3
2R
R
AF 
Condition on gain AF<2Q2

55. 55
Notch filter

58. Shunted Twin T Filter
with swapped R & C

59. ALL PASS FILTER:
It is a special type of filter which passes all the
frequency components of the input signal to output
without any attenuation. But it introduces a
predictable phase shift for different frequency of
the input signal.

60. The all pass
filters are
also called
as delay
equalizers
or phase
correctors.

61. Switched-Capacitor Filters
• Active RC filters are difficult to implement totally on
an IC due to the requirements of large valued capacitors
and accurate RC time constants
• The switched capacitor filter technique is based on the
realization that a capacitor switched between two
circuit nodes at a sufficiently high rate is equivalent to a
resistor connecting these two nodes.
• Switched capacitor filter ICs offer a low cost high order
filter on a single IC.
• Can be easily programmed by changing the clock
frequency.

62. R
iv1
+
-
v2
+
-
R
vv
i
21 

i
vv
R
21 

v1
+
-
v2
+
-
S1 S2
CR
q1 = CRv1
q2 = CRv2
Dq = q1-q2 = CR(v1-v2)
Switched-Capacitor Filters

63. Copyright © S.Witthayapradit.2009
T
T
1
fC 
v1
+
-
Requ
v2
+
-
 21 vvCfqf
T
q
i RCC 


RC
21
equ
Cf
1
i
vv
R 


the value of R is a function of CR and fC. For a
fixed value of C, the value of R can be adjusted by
adjusting fC

64. Zeros: roots of N(s)
• Poles: roots of D(s)
• Poles must be in the left half plane for the system to be stable
• As the poles get closer to the boundary, the system becomes less stable
• Pole-Zero Plot: plot of the zeros and poles on the complex s plane
H(s) =
𝑵(𝒔)
𝑫(𝒔)
X
X
X
X X
X
X
X
X
-a +a
RealImaginary
jω
-jω
𝒌
𝒔 + 𝒂
𝒌
𝒔 − 𝒂