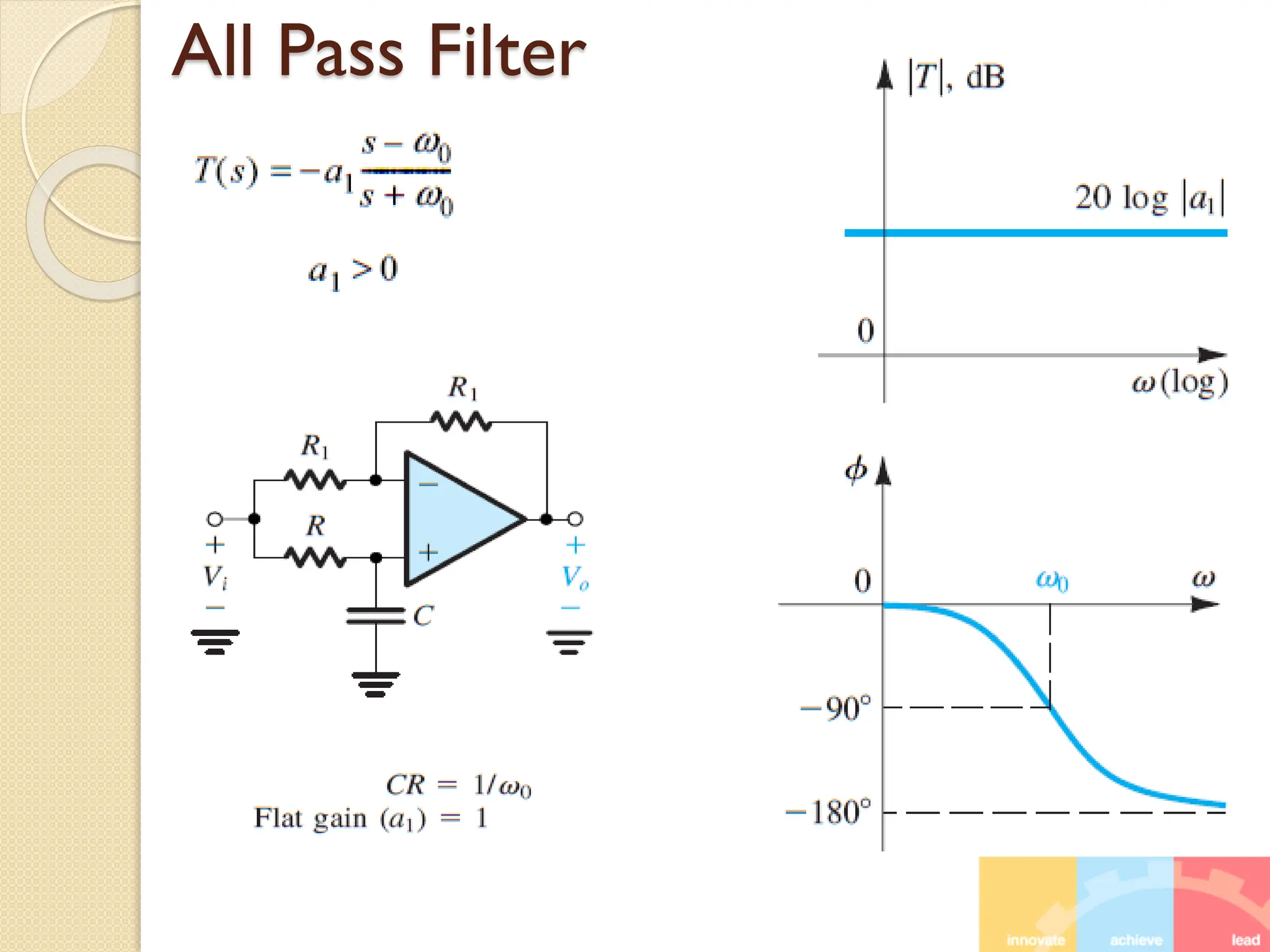
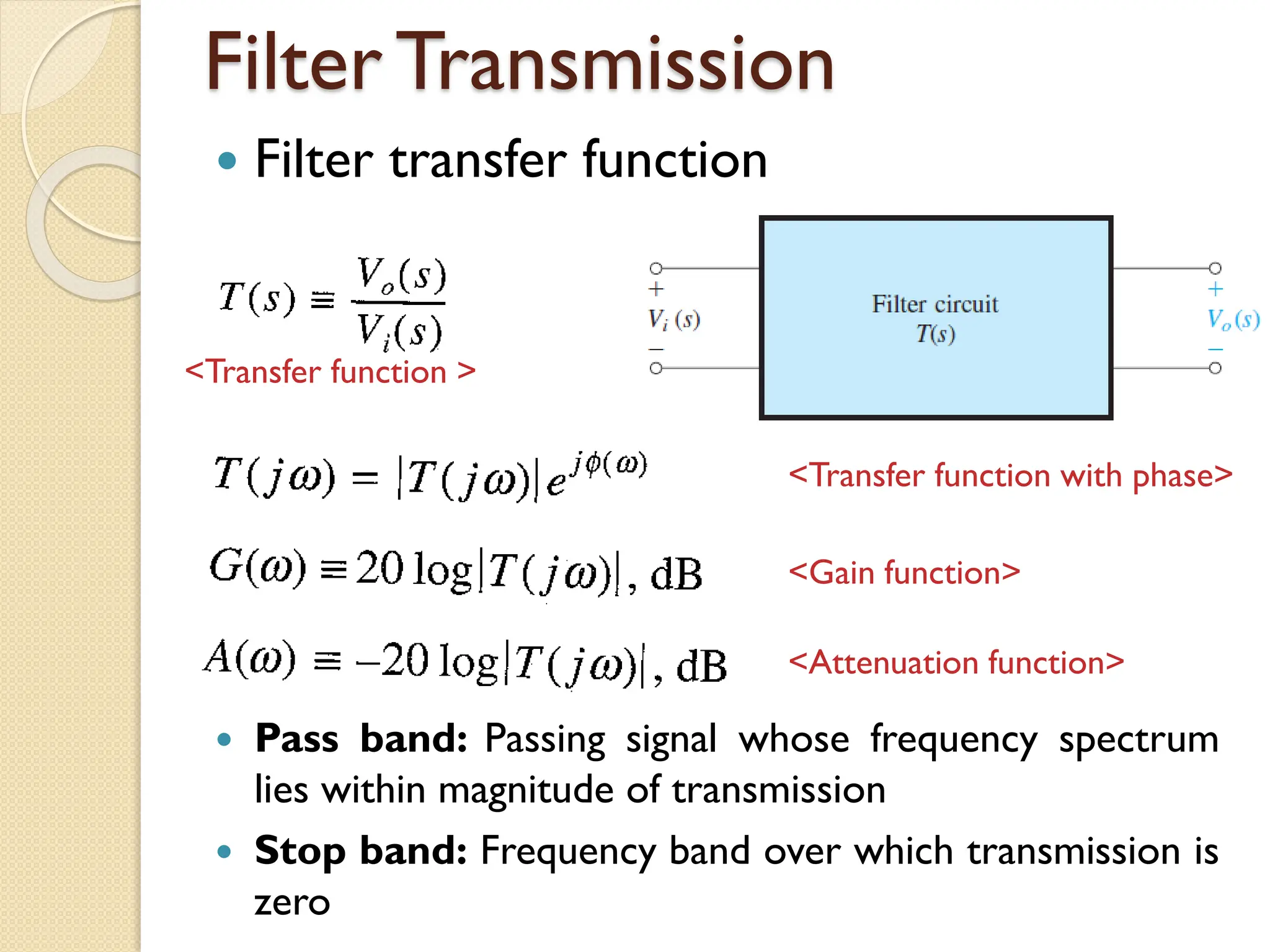
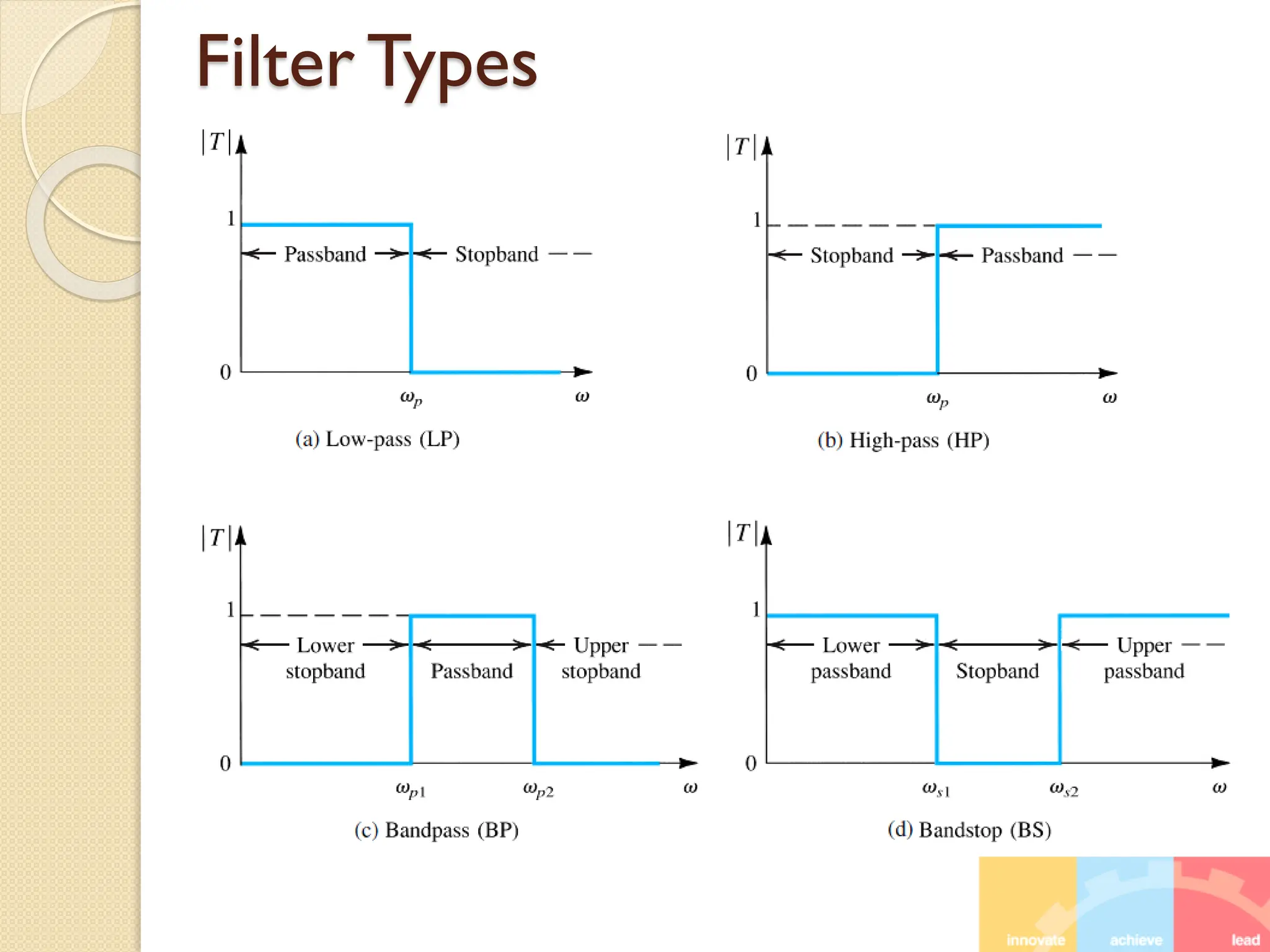
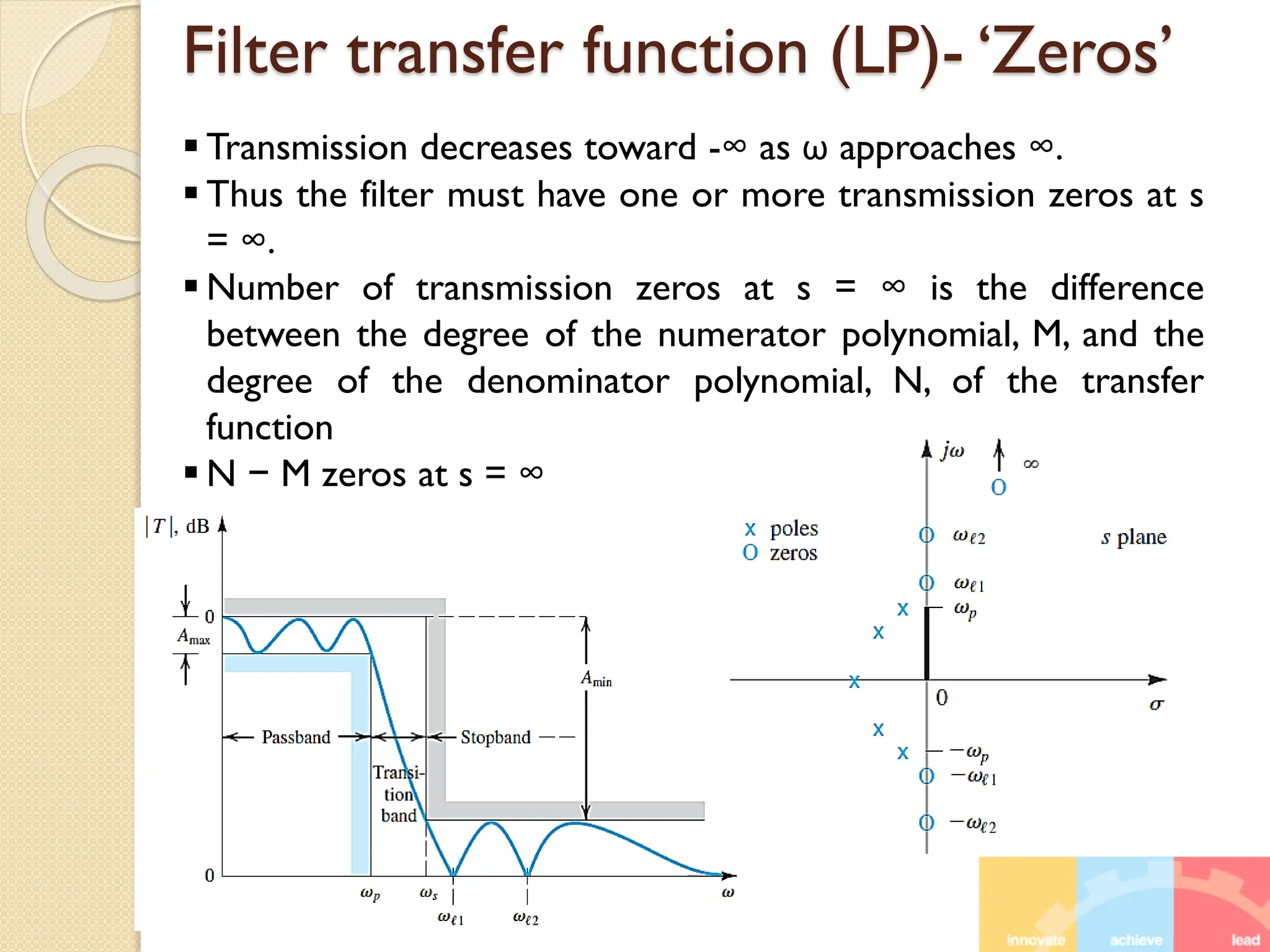
5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf5 Filter Part 2 (Lecture 19, 20, 21, 22).pdf









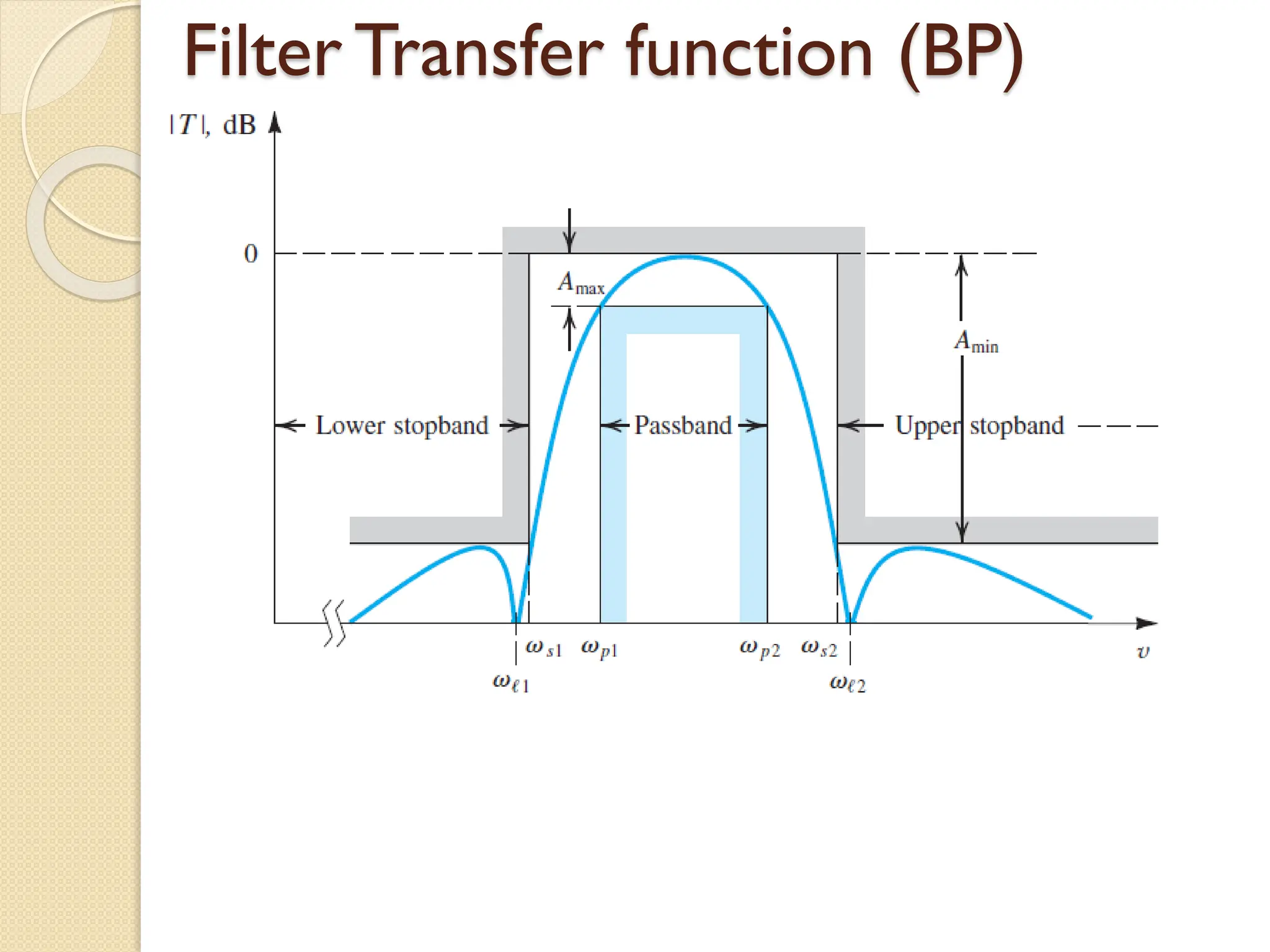
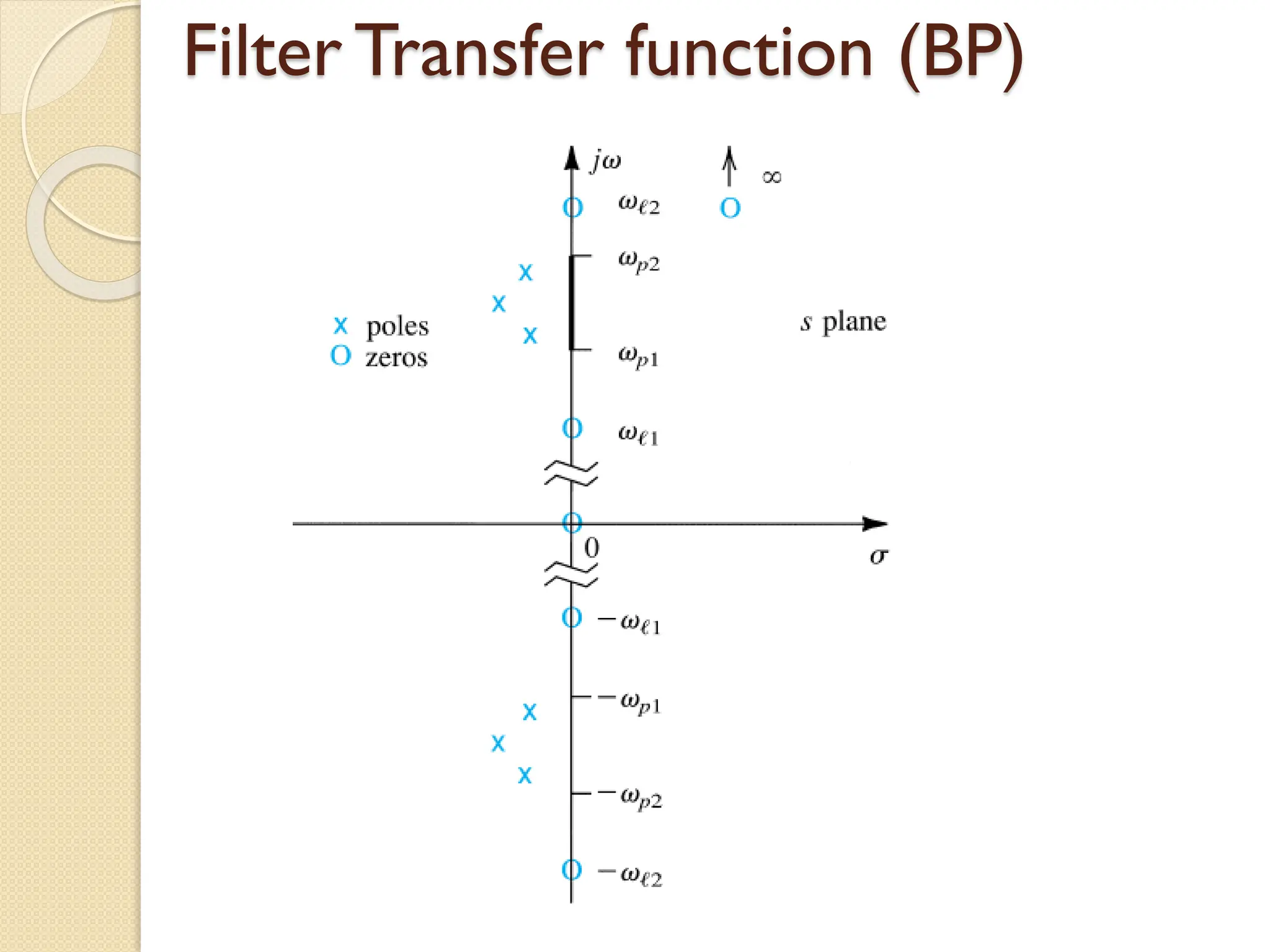

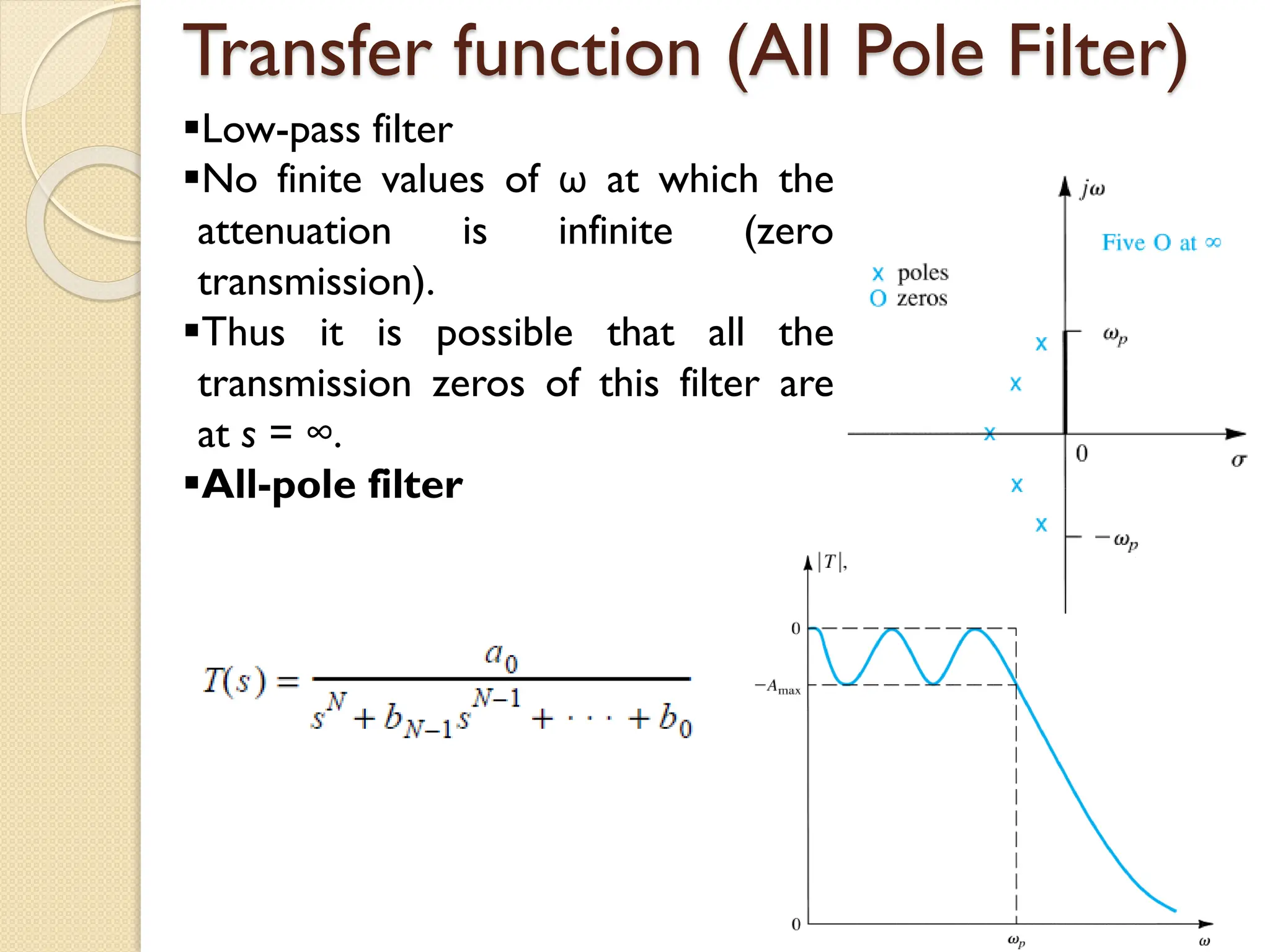
![Problem 1
A second order filter has its poles at s = [-1/2 ±j(√3/2)].
The transmission is zero at w=2 rad/s and is unity at DC
(w=0). Find the transfer function](https://image.slidesharecdn.com/5filterpart1161718-250302192144-8943d9d8/75/5-Filter-Part-1-16-17-18-pdf5-Filter-Part-2-Lecture-19-20-21-22-pdf5-Filter-Part-2-Lecture-19-20-21-22-pdf5-Filter-Part-2-Lecture-19-20-21-22-pdf-17-2048.jpg)