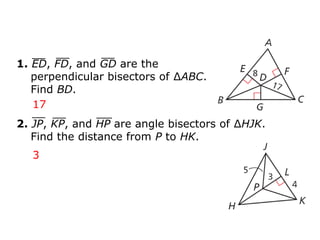
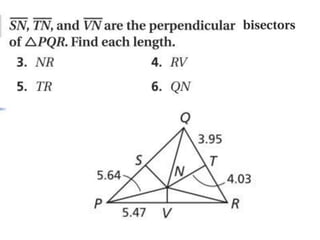
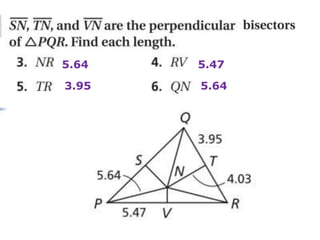
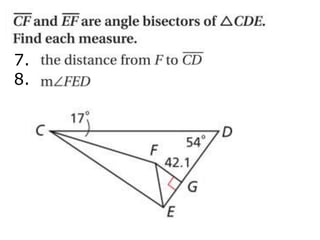
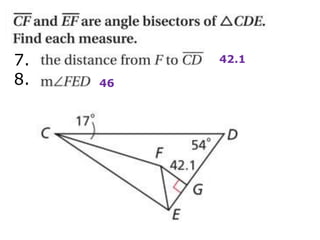
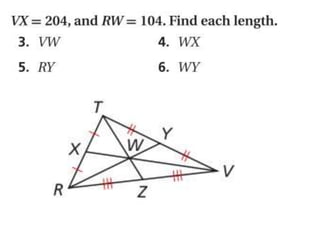
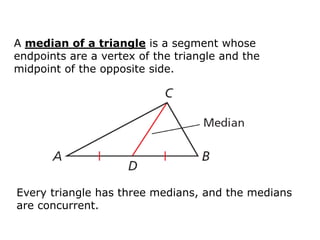
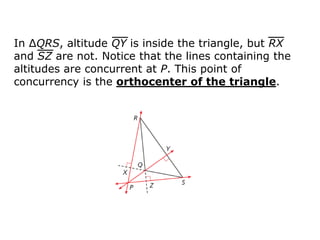
1. The document is a geometry drill from December 17, 2013 that contains problems about triangle properties like perpendicular bisectors, angle bisectors, circumcenters, medians, altitudes, centroids, and orthocenters. 2. Key terms defined include median, centroid, altitude, and orthocenter of a triangle. 3. The document provides explanations of medians, altitudes, centroids, and orthocenters of triangles and their properties.

1. GT Geometry Drill 12/17/13
• Pick up a 2 pieces of patty paper

2. 1. ED, FD, and GD are the
perpendicular bisectors of ∆ABC.
Find BD.
17
2. JP, KP, and HP are angle bisectors of ∆HJK.
Find the distance from P to HK.
3

4. 5.64
5.47
3.95
5.64

5. 7.
8.

6. 7.
8.
42.1
46

7. Find the circumcenter given the
following vertices of the triangle

8. Find the circumcenter given the
following vertices of the triangle
(-3.5, -5)

9. Objectives
Apply properties of medians of a
triangle.
Apply properties of altitudes of a
triangle.

10. Vocabulary
median of a triangle
centroid of a triangle
altitude of a triangle
orthocenter of a triangle

11. A median of a triangle is a segment whose
endpoints are a vertex of the triangle and the
midpoint of the opposite side.
Every triangle has three medians, and the medians
are concurrent.

12. The point of concurrency of the medians of a triangle
is the centroid of the triangle . The centroid is
always inside the triangle. The centroid is also called
the center of gravity because it is the point where a
triangular region will balance.

13. An altitude of a triangle is a perpendicular segment
from a vertex to the line containing the opposite side.
Every triangle has three altitudes. An altitude can be
inside, outside, or on the triangle.

14. In ΔQRS, altitude QY is inside the triangle, but RX
and SZ are not. Notice that the lines containing the
altitudes are concurrent at P. This point of
concurrency is the orthocenter of the triangle.

15. vocabulary
The midsegment of a
triangle - Segment that
joins the midpoints of
any two sides of a
triangle.

16. Triangle Midsegment

17. Theorem
The midsegment of a
triangle is half the
length of, and
parallel to, the third
side of a triangle.

19. Find the orthocenter of a triangle
with the given vertices