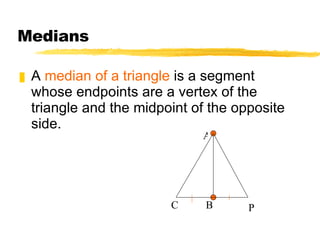
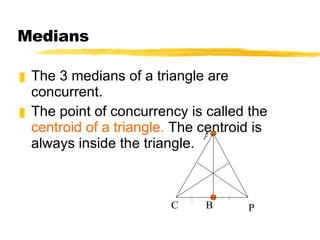
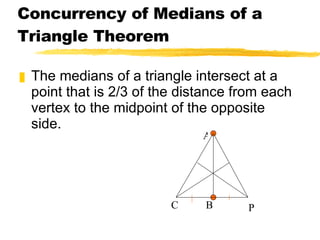
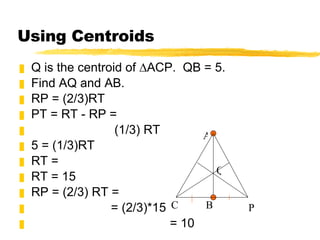
- The three medians of a triangle intersect at the centroid, which is located 2/3 of the distance from each vertex to the midpoint of the opposite side.
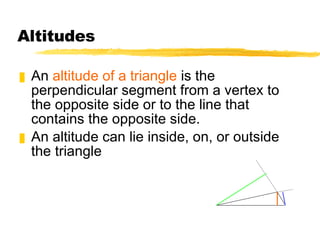
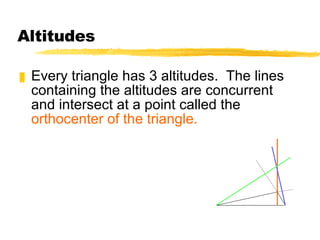
- The three altitudes of a triangle are concurrent at the orthocenter, which can lie inside, on, or outside the triangle depending on whether the triangle is acute, right, or obtuse.
- A midsegment connects the midpoints of two sides of a triangle. The midsegment is parallel to the third side and is half as long based on the Midsegment Theorem.