The document discusses recursive equations and dynamic programming. It covers formulating recursive equations for multistage decision processes in both a backward and forward manner. Specifically, it explains how to write recursive equations first for the final stage and then proceeding backwards to the first stage for backward recursion. For forward recursion, it discusses solving the problem by starting from the first stage and proceeding towards the last stage. The key objectives are to break down a multistage problem into single stage subproblems and solve them sequentially using recursive equations and the principle of optimality.

1. D Nagesh Kumar, IISc Optimization Methods: M5L21
Dynamic Programming
Recursive Equations

2. D Nagesh Kumar, IISc Optimization Methods: M5L22
Introduction and Objectives
Introduction
Recursive equations are used to solve a problem in sequence
These equations are fundamental to the dynamic programming
Objectives
To formulate recursive equations for a multistage decision
process
In a backward manner and
In a forward manner

3. D Nagesh Kumar, IISc Optimization Methods: M5L23
Recursive Equations
Recursive equations are used to structure a multistage decision
problem as a sequential process
Each recursive equation represents a stage at which a decision
is required
A series of equations are successively solved, each equation
depending on the output values of the previous equations
A multistage problem is solved by breaking into a number of
single stage problems through recursion
Approached can be done in a backward manner or in a forward
manner

4. D Nagesh Kumar, IISc Optimization Methods: M5L24
Backward Recursion
A problem is solved by writing equations first for the final stage and
then proceeding backwards to the first stage
Consider a serial multistage problem
Let the objective function for this problem is
Stage 1 Stage t Stage T
St
NBt
Xt
S1 S2
NB1 NBT
X1 XT
ST ST+1St+1
( )
( ) ( ) ( ) ( ) ( ) 1...(,,...,...,,
,
111222111
1 1
TTTTTTttt
T
t
T
t
tttt
SXhSXhSXhSXhSXh
SXhNBf
++++++=
==
−−−
= =
∑ ∑

5. D Nagesh Kumar, IISc Optimization Methods: M5L25
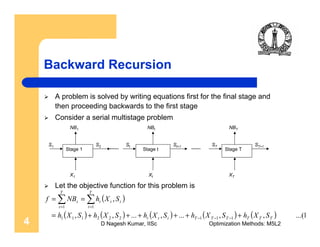
Backward Recursion …contd.
The relation between the stage variables and decision variables are
St+1 = g(Xt, St), t = 1,2,…, T.
Consider the final stage as the first sub-problem. The input variable to
this stage is ST.
Principle of optimality: XT should be selected such that is
optimum for the input ST
The objective function for this stage is
Next, group the last two stages together as the second sub-problem.
The objective function is
( )TTT SXh ,
∗
Tf
( )[ ]TTT
X
TT SXhoptSf
T
,)( =∗
( ) ( )[ ]TTTTTT
XX
TT SXhSXhoptSf
TT
,,)( 111
,
11
1
+= −−−−
∗
−
−

6. D Nagesh Kumar, IISc Optimization Methods: M5L26
Backward Recursion …contd.
By using the stage transformation equation, can be rewritten
as
Thus, a multivariate problem is divided into two single variable
problems as shown
In general, the i+1th sub-problem can be expressed as
Converting this to a single variable problem
)( 11 −
∗
− TT Sf
( ) ( )( )[ ]11111111 ,,)(
1
−−−
∗
−−−−
∗
− +=
−
TTTTTTT
X
TT SXgfSXhoptSf
T
( ) ( ) ( )[ ]TTTTTTiTiTiT
XXX
iTiT SXhSXhSXhoptSf
TTiT
,,...,)( 111
,,..., 1
+++= −−−−−−−
∗
−
−−
( ) ( )( )[ ]iTiTiTiTiTiTiT
X
iTiT SXgfSXhoptSf
iT
−−−
∗
−−−−−−
∗
− +=
−
,,)( )1(

7. D Nagesh Kumar, IISc Optimization Methods: M5L27
Backward Recursion …contd.
denotes the optimal value of the objective function for
the last i stages
Principle of optimality for backward recursion can be stated as,
No matter in what state of stage one may be, in order
for a policy to be optimal, one must proceed from that
state and stage in an optimal manner sing the stage
transformation equation
∗
−− )1(iTf

8. D Nagesh Kumar, IISc Optimization Methods: M5L28
Forward Recursion
The problem is solved by starting from the stage 1 and proceeding
towards the last stage
Consider a serial multistage problem
Let the objective function for this problem is
Stage 1 Stage t Stage T
St
NBt
Xt
S1 S2
NB1 NBT
X1 XT
ST ST+1St+1
( )
( ) ( ) ( ) ( ) ( ) 1...(,,...,...,,
,
111222111
1 1
TTTTTTttt
T
t
T
t
tttt
SXhSXhSXhSXhSXh
SXhNBf
++++++=
==
−−−
= =
∑ ∑

9. D Nagesh Kumar, IISc Optimization Methods: M5L29
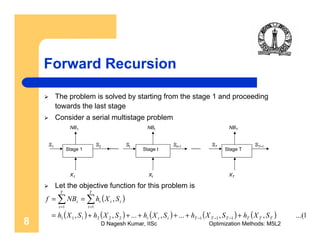
Forward Recursion …contd.
The relation between the stage variables and decision variables are
where St is the input available to the stages 1 to t
Consider the stage 1 as the first sub-problem. The input variable to
this stage is S1
Principle of optimality: X1 should be selected such that is
optimum for the input S1
The objective function for this stage is
( ) TtSXgS ttt ,....,2,1, 11 =′= ++
( )111 ,SXh
∗
1f
( )[ ]11111 ,)(
1
SXhoptSf
X
=∗

10. D Nagesh Kumar, IISc Optimization Methods: M5L210
Backward Recursion …contd.
Group the first and second stages together as the second sub-
problem. The objective function is
By using the stage transformation equation, can be rewritten
as
In general, the ith sub-problem can be expressed as
( ) ( )[ ]111222
,
22 ,,)(
12
SXhSXhoptSf
XX
+=∗
)( 22 Sf ∗
( ) ( )( )[ ]222122222 ,,)(
2
SXgfSXhoptSf
X
′+= ∗∗
( ) ( ) ( )[ ]111222
,...,,
,,...,)(
21
SXhSXhSXhoptSf iii
XXX
ii
i
+++=∗

11. D Nagesh Kumar, IISc Optimization Methods: M5L211
Backward Recursion …contd.
Converting this to a single variable problem
denotes the optimal value of the objective function for the
last i stages
Principle of optimality for forward recursion can be stated as,
No matter in what state of stage one may be, in order
for a policy to be optimal, one had to get to that state
and stage in an optimal manner
( ) ( )( )[ ]iiiiiii
X
ii SXgfSXhoptSf
i
,,)( )1(
′+= ∗
−
∗
∗
if

12. D Nagesh Kumar, IISc Optimization Methods: M5L212
Thank You