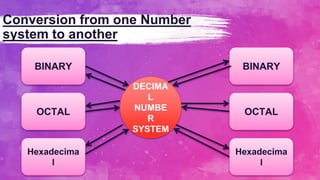
This document discusses different number systems used in computers, including positional and non-positional systems. It describes the binary, decimal, octal, and hexadecimal positional number systems, explaining that each has a base and allowable digits. Converting between number systems involves determining the positional value of each digit and multiplying/summing accordingly. Examples are provided for converting between binary, octal, decimal, and hexadecimal.

1. NUMBER
SYSTEM

2. Number System
 Every computer stores numbers, letters and other
specially characters In coded form. There are two
types of number system-
1) Non-Positional Number system
2) Positional Number System

3. Non-Positional Number system
✔ In this number system, we have symbols as I for 1, II
for 2, III for 3, IIII for 4 etc. each symbols represents
the same value regardless of its position in a
number.

4. Positional Number system
✔ In this system, there are only a few symbols can digits.
These symbols represent different values. Depending
upon the position they occupy in a number is
determined by three consideration-
1) The digit itself
2) The position of a digit in the number
3) The base of the number

5. Positional Number System
1) Binary Number System
2) Decimal Number system
3) Octal Number System
4) Hexadecimal Number System

6. Decimal Number System
 In our day-to-day life we use decimal number. In this
system, base is equal to 10 because there are all
together 10 symbols or digits (0,1,2,3,4,5,6,7,8,9).
The largest single digit is 9 that is 1 less than the
base 10.
Example- (2431)10 , (9671)10 etc.

7. Binary Number System
 Binary number system is like decimal number system
except that the base is 2, instead of 10. we can use
only 2 symbols or digits (0 and 1) in this number
system. The largest single digit is 1 that is 1 less than
the base 2.
Example- (10101)2 , (101101)2 etc.

8. Octal Number System
 In Octal number system, the base is 8, and there are
only 8 symbols or digits (0,1,2,3,4,5,6,7) in this
number system. The largest single digit is 7 that is 1
less than the base 8.
Example- (3457)8 , (101020)8, (101110)8 etc.

9. Hexadecimal Number
System
 In Hexadecimal number system, the base is 16, and
there are only 16 symbols or digits
(0,1,2,3,4,5,6,7,8,9,) and remaining are denoted by
the symbols (A,B,C,D,E,F) representing decimal
values 10,11,12,13,14,15 respectively. The largest
single digit is F or 15 that is 1 less than the base 16.
Example- (3457)16 , (1A0F)16, (6AC5)16 etc.

10. Conversion from one Number
system to another
DECIMA
L
NUMBE
R
SYSTEM
BINARY
OCTAL
Hexadecima
l
BINARY
OCTAL
Hexadecima
l

11. Converting from another base to
Decimal
1) Determined the positional value of each digit.
2) Multiply the obtained column(positional) values by the
digits. In the corresponding column.
3) Sum up the product calculated in step 2. the total is
equivalent value in decimal.

12. Check Number-
1) 123478 ?
2) (101011)8 ?
3) (1AF9) ?

13. Examples (Binary to decimal)
1) (11001)2 = ( ? )10
 (1X24 + 1X23 + 0X22 + 0X21 + 1X20 )
 (1X2X2X2X2 + 1X2X2X2 + 0X2X2 + 0X2 +1X1)
 (16 + 8 + 0 + 0 + 1)
 (25) 10

14. Examples (Octal to decimal)
1) (4706)8 = ( ? )10
 (4X83 + 7X82 + 0X81 + 6X80 ) 10
 (4X8X8X8 + 7X8X8 + 0X8 + 6X1) 10
 (2048 + 448 + 0 + 6) 10
 (2502)10

15. Examples (Hexadecimal to
decimal)
1) (1AC)16 = ( ? )10
 (1X162 + AX161 + CX160 ) 10
 (1X16X16 + 10X16 + 12X1) 10
 (256 + 160 + 12) 10
 (428)10

16. Examples For your Practice-
1) (9FA)16 = ( ? )10
2) (1110)2 = ( ? )10
3) (274)8 = ( ? )10
Solve these Question and give answer in comment box.

17. THANKSS
…