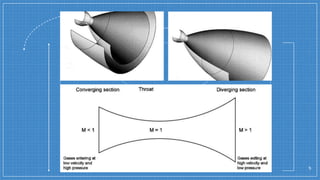
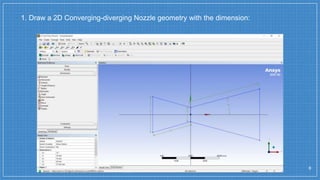
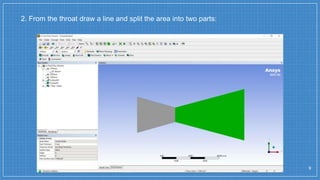
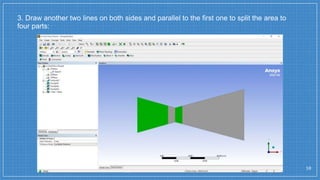
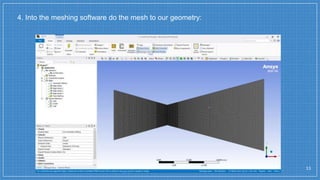
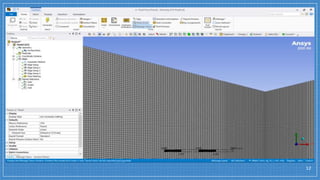
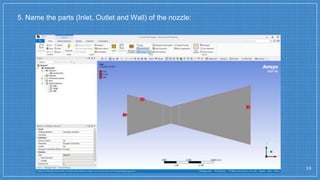
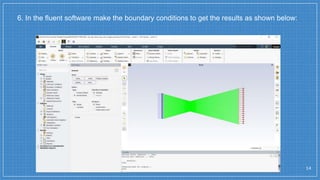
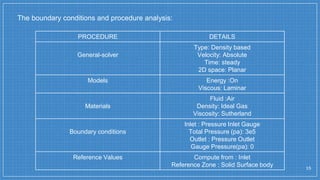
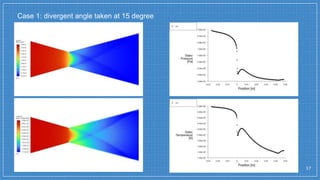
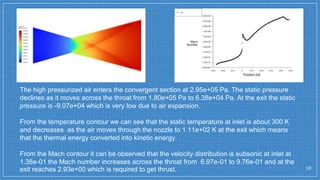
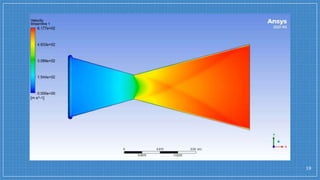
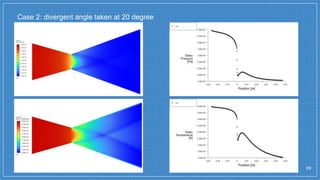
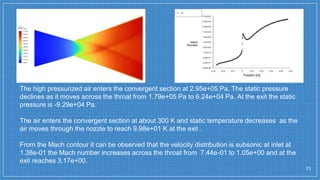
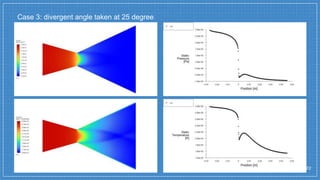
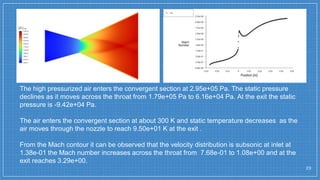
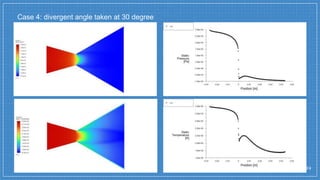
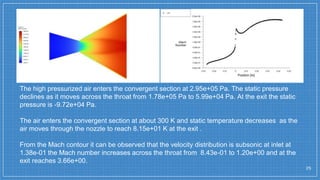
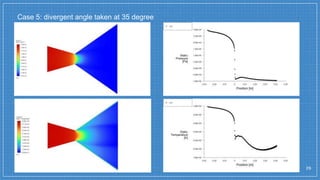
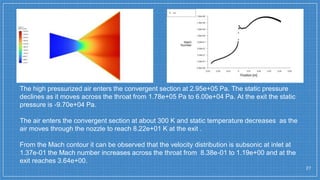
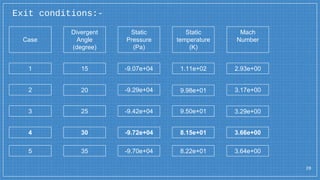
The document summarizes a simulation of a convergent-divergent rocket nozzle using computational fluid dynamics (CFD) analysis. It discusses the aims of analyzing flow parameters like pressure and temperature inside converging-divergent and conical nozzles. It then analyzes 5 cases of converging-divergent nozzles with divergent angles from 15 to 35 degrees. The results show that static pressure decreases and Mach number increases with larger divergent angles, with the optimum angle being 30 degrees where Mach number reaches 3.66.

1. Simulation of convergent divergent
rocket nozzle using CFD analysis
By
Almukhtar A. Farhan
Supervised By
Dr. Iman Jabbar Ooda
University of Baghdad-College of Engineering
Aeronautical Engineering Department

2. INTRODUCTION:-
Rocket engines are reaction engines, manufacturing thrust by ejecting mass rearward, in
accordance with Newton's third law which could be an automation that is meant to
manage the speed of flow, speed direction and pressure of stream that exhaust through
the nozzle of that rocket. Most rocket engines use the combustion of reactive chemicals
to provide the mandatory energy, however non-combusting forms like cold gas thrusters
and nuclear thermal rockets additionally exist.
The nozzle is the final part of rockets that has the capacity to convert the thermo-
chemical energy generated in the combustion chamber into kinetic energy in order to
produce thrust by converting the low velocity, high pressure, high temperature (subsonic)
gases in the combustion chamber into high velocity (supersonic) gases of lower pressure
and temperature. The design of a nozzle including divergent angle and other parameters
has particular importance in determining the thrust and performance of a rocket..
2

3. There are many types of nozzles that usually used in rocket
engines and some of them are mentioned below.
3
• Cone (conical) nozzle:
• Bell (contoured) nozzle:
• Annular (plug) nozzle:
• Extendible nozzle
Convergent-Divergent Nozzle (De Laval Nozzle): -
Which is developed by Swedish inventor Gustaf de Laval in 1888 while he was trying to
develop a more efficient steam engine. It is a tube that pinched in the middle, making a
carefully balanced, asymmetric hourglass shape usually used if the nozzle pressure
ratio is high. it is used to accelerate a compressible fluid to supersonic speeds in the axial
direction, by converting the thermal energy of the flow into kinetic energy, where the flow
is accelerated from low subsonic to sonic velocity at the throat and further expanded to
supersonic velocity at the exit

4. Conical nozzle: -
4
Conical nozzles have a constant expansion rate and look like a cone, hence their name.
These nozzles tend to be the long and heavy in compare with other types of nozzles. They
do have the advantage however of being easy to manufacture and its simple cone shape
for design, and it contains no inflection as the propellants are expelled from the
combustion chamber. This lack of inflection is critical for solid and hybrid engines because
these types of engines usually have some pieces of solid propellant expelled all the way
out of the nozzle. Therefore, a conical nozzle is desired for solid and hybrid propellant
types due to the lack of inflection..

5. 5

6. AIMS OF THE PROJECT:-
6
1. This project aims to analyze the variation of flow parameters like pressure, temperature
and Mach number inside a converging-diverging nozzle and conical nozzle.
2. Study the effect of divergent angle on the flow inside the converging-diverging nozzle.
3. Study the effect of the divergent angle on the flow inside the conical nozzle.

7. THEORETICAL ANALYSIS:-
7
Computational fluid dynamics (CFD) is engineering tool that access experimentation to
solve engineering problems by using various methods like analytical method and
experimental methods using prototypes. The analytical method is very complicated and
difficult. And the experimental methods are very costly. Prototype testing has to be error
detected from design to made another prototype. So, time and cost consuming are high.
Thus, the difficulties rectified by using CFD. In the CFD a problem is simulated in
software and transport equation associated with the problem is mathematically solved
along with computer assistance. Thus, we would be able to predict the results of a
problem before experimentation. The CFD proves for efficient tool and also analysis of
various flow parameters
Following steps made by using Ansys Fluent software and repeated for each angle 15,
20, 25, 30, 35 to get the results and by comparison we will be able to obtain the best
divergent angle which provides the maximum velocity for the flow at the exit of the nozzle
to chose it as design angle.

8. 1. Draw a 2D Converging-diverging Nozzle geometry with the dimension:
8

9. 2. From the throat draw a line and split the area into two parts:
9

10. 3. Draw another two lines on both sides and parallel to the first one to split the area to
four parts:
10

11. 4. Into the meshing software do the mesh to our geometry:
11

12. 12

13. 5. Name the parts (Inlet, Outlet and Wall) of the nozzle:
13

14. 6. In the fluent software make the boundary conditions to get the results as shown below:
14

15. The boundary conditions and procedure analysis:
15
PROCEDURE DETAILS
General-solver
Type: Density based
Velocity: Absolute
Time: steady
2D space: Planar
Models Energy :On
Viscous: Laminar
Materials
Fluid :Air
Density: Ideal Gas
Viscosity: Sutherland
Boundary conditions
Inlet : Pressure Inlet Gauge
Total Pressure (pa): 3e5
Outlet : Pressure Outlet
Gauge Pressure(pa): 0
Reference Values Compute from : Inlet
Reference Zone : Solid Surface body

16. RESULTS AND DISCUSSIONS:-
16
By using DesignModeler, five different dimensional designs are modeled by changing the
divergent angle and then CFD analysis is done for five different models and the variation
in Mach number, static temperature and static pressure is being observed in each case.

17. Case 1: divergent angle taken at 15 degree
17

18. 18
The high pressurized air enters the convergent section at 2.95e+05 Pa. The static pressure
declines as it moves across the throat from 1.80e+05 Pa to 6.38e+04 Pa. At the exit the static
pressure is -9.07e+04 which is very low due to air expansion.
From the temperature contour we can see that the static temperature at inlet is about 300 K
and decreases as the air moves through the nozzle to 1.11e+02 K at the exit which means
that the thermal energy converted into kinetic energy.
From the Mach contour it can be observed that the velocity distribution is subsonic at inlet at
1.38e-01 the Mach number increases across the throat from 6.97e-01 to 9.76e-01 and at the
exit reaches 2.93e+00 which is required to get thrust.

19. 19

20. Case 2: divergent angle taken at 20 degree
20

21. 21
The high pressurized air enters the convergent section at 2.95e+05 Pa. The static pressure
declines as it moves across the throat from 1.79e+05 Pa to 6.24e+04 Pa. At the exit the static
pressure is -9.29e+04 Pa.
The air enters the convergent section at about 300 K and static temperature decreases as the
air moves through the nozzle to reach 9.98e+01 K at the exit .
From the Mach contour it can be observed that the velocity distribution is subsonic at inlet at
1.38e-01 the Mach number increases across the throat from 7.44e-01 to 1.05e+00 and at the
exit reaches 3.17e+00.

22. Case 3: divergent angle taken at 25 degree
22

23. 23
The high pressurized air enters the convergent section at 2.95e+05 Pa. The static pressure
declines as it moves across the throat from 1.79e+05 Pa to 6.16e+04 Pa. At the exit the static
pressure is -9.42e+04 Pa.
The air enters the convergent section at about 300 K and static temperature decreases as the
air moves through the nozzle to reach 9.50e+01 K at the exit .
From the Mach contour it can be observed that the velocity distribution is subsonic at inlet at
1.38e-01 the Mach number increases across the throat from 7.68e-01 to 1.08e+00 and at the
exit reaches 3.29e+00.

24. Case 4: divergent angle taken at 30 degree
24

25. 25
The high pressurized air enters the convergent section at 2.95e+05 Pa. The static pressure
declines as it moves across the throat from 1.78e+05 Pa to 5.99e+04 Pa. At the exit the static
pressure is -9.72e+04 Pa.
The air enters the convergent section at about 300 K and static temperature decreases as the
air moves through the nozzle to reach 8.15e+01 K at the exit .
From the Mach contour it can be observed that the velocity distribution is subsonic at inlet at
1.38e-01 the Mach number increases across the throat from 8.43e-01 to 1.20e+00 and at the
exit reaches 3.66e+00.

26. Case 5: divergent angle taken at 35 degree
26

27. 27
The high pressurized air enters the convergent section at 2.95e+05 Pa. The static pressure
declines as it moves across the throat from 1.78e+05 Pa to 6.00e+04 Pa. At the exit the static
pressure is -9.70e+04 Pa.
The air enters the convergent section at about 300 K and static temperature decreases as the
air moves through the nozzle to reach 8.22e+01 K at the exit .
From the Mach contour it can be observed that the velocity distribution is subsonic at inlet at
1.37e-01 the Mach number increases across the throat from 8.38e-01 to 1.19e+00 and at the
exit reaches 3.64e+00.

28. Exit conditions:-
28
Case
1
3
2
4
5
Divergent
Angle
(degree)
Static
Pressure
(Pa)
Static
temperature
(K)
Mach
Number
15 -9.07e+04 1.11e+02 2.93e+00
20 9.98e+01
-9.29e+04 3.17e+00
25 9.50e+01 3.29e+00
-9.42e+04
30 -9.72e+04 8.15e+01 3.66e+00
35 -9.70e+04 8.22e+01 3.64e+00

29. 29
The outcomes from the analysis on the rocket nozzle with varying divergent angle are
as follows
 At the divergent section, the velocity distribution is found to be increasing with
increase in divergent angle.
 The static pressure decreased with increasing in divergent angle at exit section.
 The static temperature decreased with increasing in divergent angle at exit section.
 Mach number of optimum value for this geometry is obtained at divergent angle of
30° which is 3.66e+00
Conclusions:-

30. 30
Thank you for listening