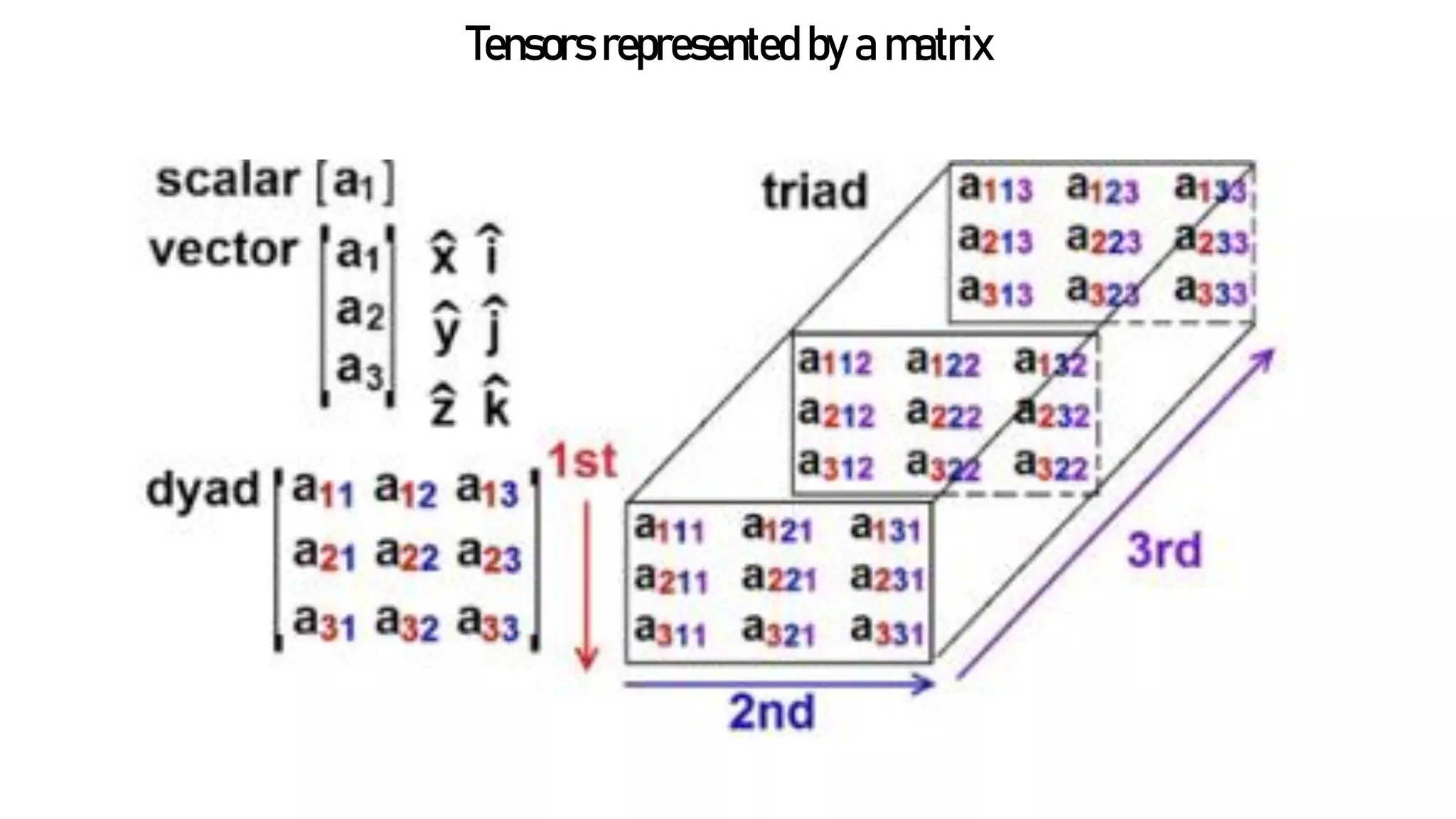
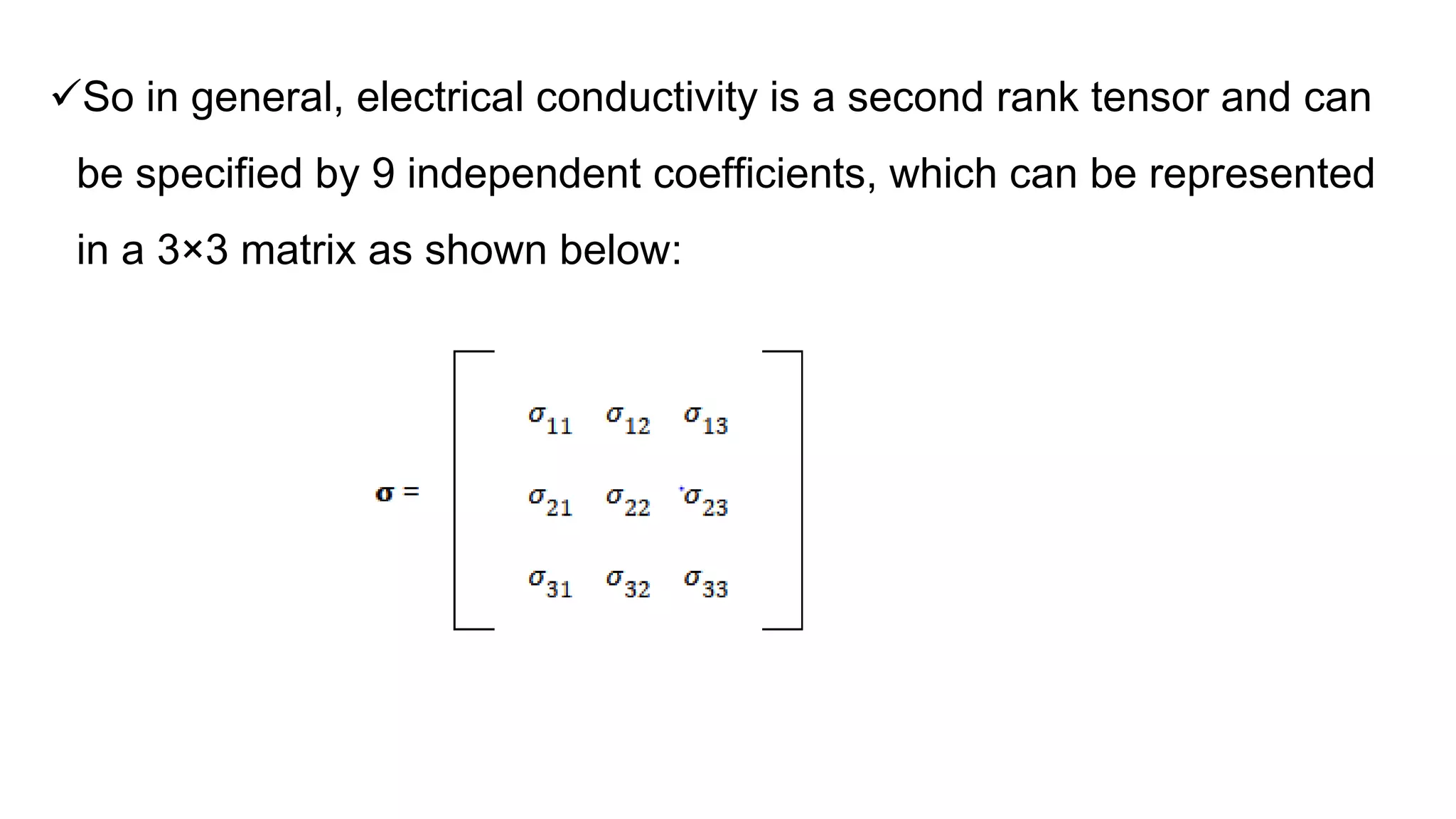
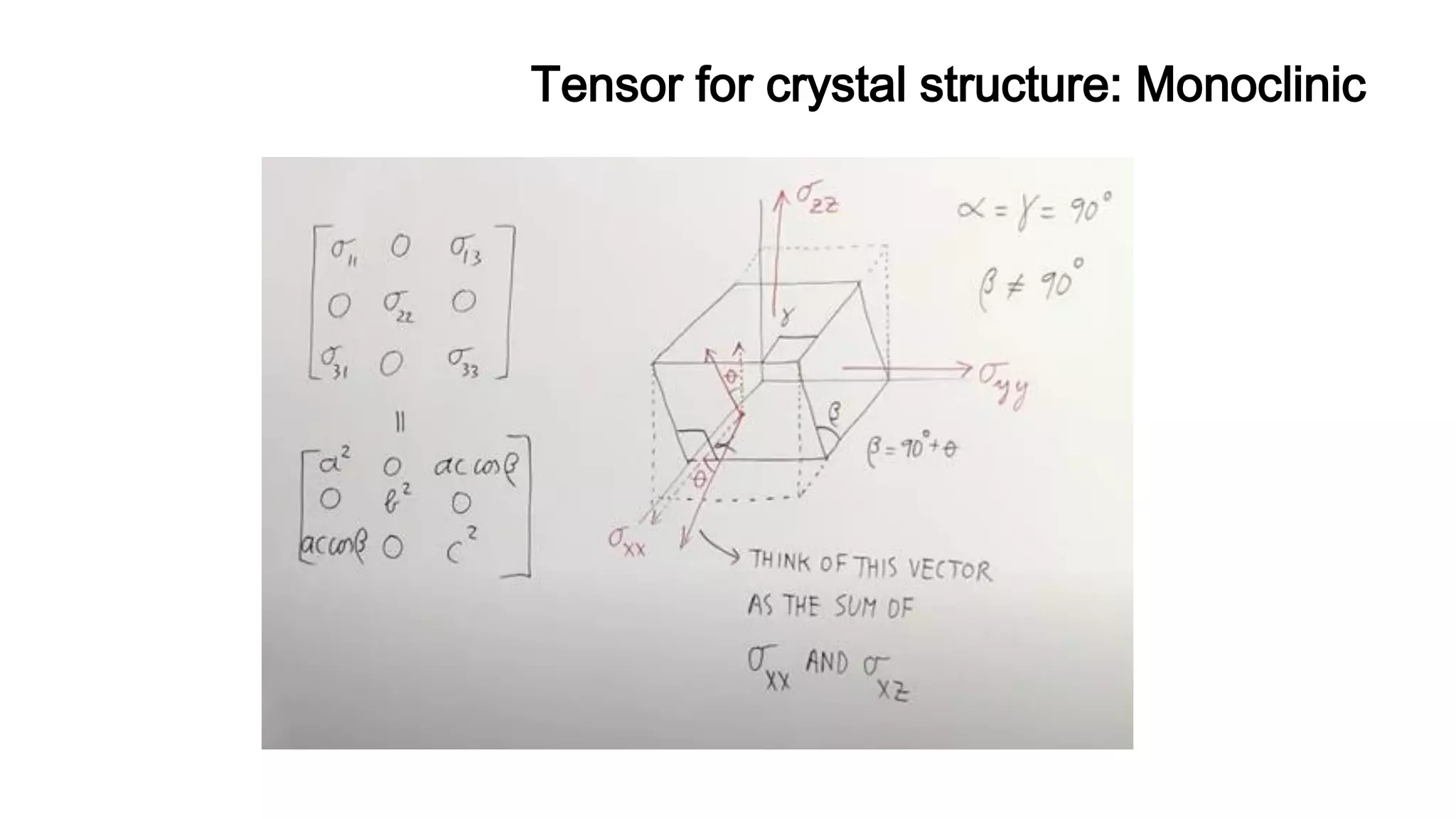
Vectors, tensors, and their operations are important concepts in transport phenomena. Vectors describe quantities with magnitude and direction, such as velocity and force. Tensors, such as stress and momentum flux, are higher-order quantities represented by matrices. Common vector operations include addition, subtraction, and multiplication by scalars. The scalar product yields a scalar from two vectors, while the vector product yields another vector. Tensors are useful for describing physical properties of materials that depend on orientation, such as electrical conductivity.

1. Vector and Tensor

2. Vector and Tensor Notation
The physical quantities encountered in transport phenomena fall into
three categories:
Scalars: temperature, pressure, volume, and time
Vectors: velocity, momentum, and force
Tensors (second-order): stress, momentum flux, and velocity gradient tensors
We distinguish among these quantities by the following notation:
s = scalar (lightface Italic)
v = vector (boldface Roman)
𝜏= second-order tensor (boldface Greek)

3.  No special significance is attached to the kind of parentheses if the only
operations enclosed are addition and subtraction, or a multiplication in which ., :,
and x do not appear.
 (v . w) and (𝜏 : ∇v) are scalars
 [∇ x v] and [𝜏.v] are vectors
 {v . ∇𝜏} and { σ.𝜏 + 𝜏. σ} are second-order tensors.
 On the other hand, v - w may be written as (v - w), [v - w], or {v - w}, since no dot
or cross operations appear. Similarly vw, (vw), [vw], and {vw} are all equivalent.

6. Vector operations from a geometrical viewpoint
Definition of a vector and its magnitude
Addition and Subtraction of Vectors
The addition of two vectors can be accomplished by the familiar
parallelogram construction, as indicated below:
(a) Addition of vectors; (b) subtraction of
vectors

7. Vector addition obeys the following laws:
Commutative: (v + w) = (w + v)
Associative: (v +w) + u = v + (w +u)
Vector subtraction is performed by reversing the sign of one vector and
adding; thus v - w = v + (-w)
Multiplication of a Vector by a Scalar
When a vector is multiplied by a scalar, the magnitude of the vector is
altered but its direction is not. The following laws are applicable
Commutative: sv = vs
Associative: r(sv) = (rs)v
Distributive (q + r + s)v = qv + rv + sv

8. Scalar Product (or Dot Product) of Two Vectors
The scalar product of two vectors v and w is a scalar quantity defined
by
in which is the angle between the vectors v and w.
The scalar product is then the magnitude of w multiplied by the
projection of v on w, or vice versa
Note that the scalar product of a vector with itself is just the square of
the magnitude of the vector
Fig. Products of two vectors: (a) the scalar product;
(b) the vector product.

9. Vector Product (or Cross Product) of Two Vectors

10. Vector operations in terms of components
 In this section a parallel analytical treatment is given to each of the topics
presented geometrically. In the discussion here we restrict ourselves to
rectangular coordinates and label the axes as 1, 2, 3 corresponding to the usual
notation of x, y, z; only right-handed coordinates are used.

21. Tensors
Tensors are simply mathematical objects that can be used to describe physical
properties, just like scalars and vectors
A tensor is a mathematical representation of a scalar (tensor of rank 0, a vector
(tensor of rank 1), and a dyad (tensor of rank 2), a triad (tensor of rank 3), etc.

22. Have a number of practical applications in mathematics, science, and
engineering (stress, elasticity, fluid mechanics, crystal structure, …)
Tensor Usage in Materials Science
Lots of physical quantities of interest can be described by tensors
The tensors in the circles are those that can be applied and measured in
any orientation with respect to the crystal (e.g. stress, electric field) and are
known as field tensors
The tensors that link these properties are those that are intrinsic properties
of the crystal and must conform to its symmetry (e.g. thermal conductivity),
and are known as matter tensors

23.  The numbers in the square
brackets represent the rank of
the tensor involved

24. Tensors represented by a matrix

25. The need for second rank tensors comes when we need to consider more
than one direction to describe one of these physical properties. A good
example of this is if we need to describe the electrical conductivity of a
general, anisotropic crystal. We know that in general for isotropic
conductors that obey Ohm's law:
Which means that the current density j is parallel to the applied electric
field, E and that each component of j is linearly proportional to each
component of E. (e.g. j1 = σE1).

26. However in an anisotropic material, the current density induced will
not necessarily be parallel to the applied electric field due to preferred
directions of current flow within the crystal (a good example of this is in
graphite). This means that in general each component of the current
density vector can depend on all the components of the electric field:

27. So in general, electrical conductivity is a second rank tensor and can
be specified by 9 independent coefficients, which can be represented
in a 3×3 matrix as shown below:

28. The Dyad: A graphical representation
σ𝑥𝑥 τ𝑥𝑦 τ𝑥𝑧
τ𝑦𝑥 σ𝑦𝑦 τ𝑦𝑧
τ𝑧𝑥 τ𝑧𝑦 σ𝑧𝑧
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33

29. The Dyad: three vectors define “stress” at the three planes
σ𝑥𝑥 τ𝑥𝑦 τ𝑥𝑧
τ𝑦𝑥 σ𝑦𝑦 τ𝑦𝑧
τ𝑧𝑥 τ𝑧𝑦 σ𝑧𝑧
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33
Tx
Ty
Tz

30. Tensor for crystal structure: Orthorombic
 The vectors perpendicular to the three faces are parallel to the three axis (x,y,z)

31. Tensor for crystal structure: Monoclinic