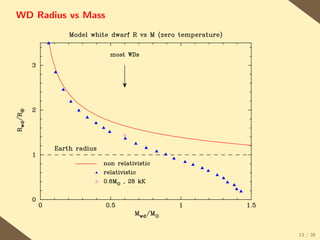
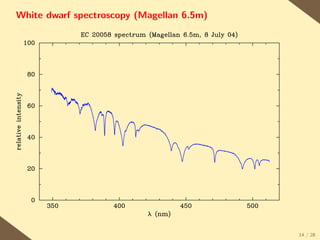
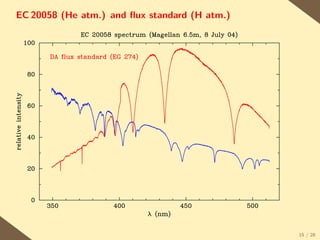
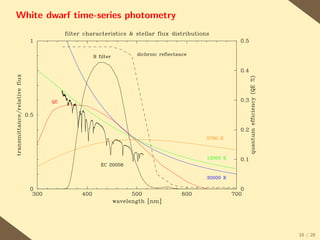
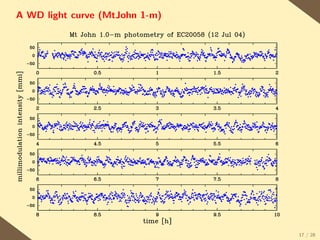
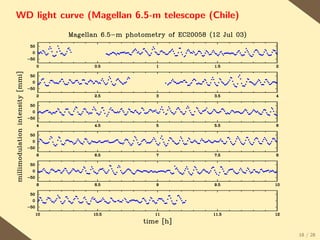
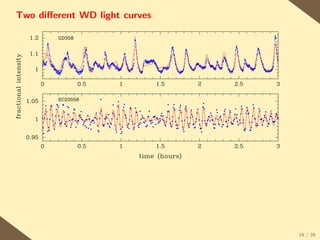
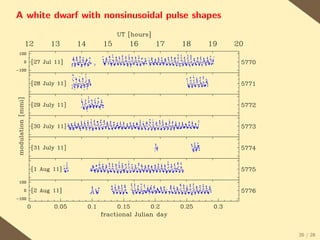
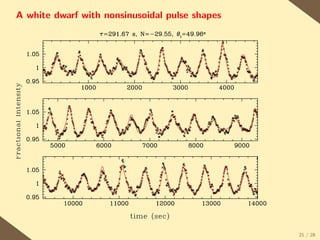
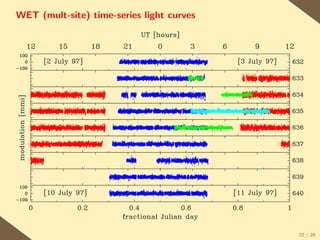
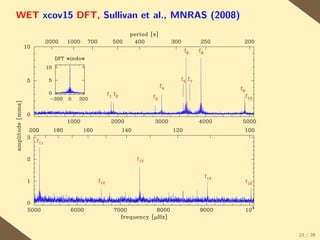
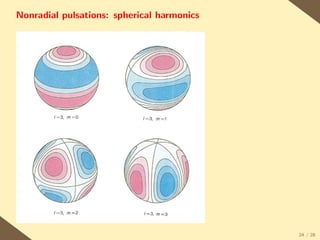
The document provides a brief history of the discovery and theoretical development of white dwarf stars from 1915 to the present. It begins by discussing how white dwarfs were first identified in 1915 and the early quantum mechanical theories developed in the 1920s to explain their structure. It then summarizes several important discoveries and theoretical advances over subsequent decades, including the prediction of a maximum white dwarf mass in 1932, the discovery of the first pulsating white dwarf in 1964, and the establishment of the Whole Earth Telescope in 1990 to facilitate extended observations of pulsating white dwarfs.

1. The Physics of White Dwarf Stars
Denis J Sullivan
Victoria University of Wellington
October 18, 2011

2. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
2 / 28

3. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
s ∼1925 Schr¨dinger, Heisenberg, Pauli, . . . quantum mechanics (QM)
o
developed.
2 / 28

4. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
s ∼1925 Schr¨dinger, Heisenberg, Pauli, . . . quantum mechanics (QM)
o
developed.
s 1926 Fowler: uses QM to develop a WD theory –
electron degeneracy pressure prevents gravitational collapse.
2 / 28

5. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
s ∼1925 Schr¨dinger, Heisenberg, Pauli, . . . quantum mechanics (QM)
o
developed.
s 1926 Fowler: uses QM to develop a WD theory –
electron degeneracy pressure prevents gravitational collapse.
s 1932 Chandrasekhar: combines special relativity (SR) with QM to
obtain a WD theory that predicts a maximum mass (∼ 1.4M )
Eddington not impressed.
2 / 28

6. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
s ∼1925 Schr¨dinger, Heisenberg, Pauli, . . . quantum mechanics (QM)
o
developed.
s 1926 Fowler: uses QM to develop a WD theory –
electron degeneracy pressure prevents gravitational collapse.
s 1932 Chandrasekhar: combines special relativity (SR) with QM to
obtain a WD theory that predicts a maximum mass (∼ 1.4M )
Eddington not impressed.
s 1964 Landolt accidentally discovers first pulsating WD (DAV,
HL Tau 76) – periodic variations ∼ 12.5 minutes in a potential WD flux
standard (Landolt, ApJ, 1968).
2 / 28

7. White dwarf & pulsating WD brief history
s 1915 Astronomers: identify white dwarfs (WDs) as unusual.
s ∼1925 Schr¨dinger, Heisenberg, Pauli, . . . quantum mechanics (QM)
o
developed.
s 1926 Fowler: uses QM to develop a WD theory –
electron degeneracy pressure prevents gravitational collapse.
s 1932 Chandrasekhar: combines special relativity (SR) with QM to
obtain a WD theory that predicts a maximum mass (∼ 1.4M )
Eddington not impressed.
s 1964 Landolt accidentally discovers first pulsating WD (DAV,
HL Tau 76) – periodic variations ∼ 12.5 minutes in a potential WD flux
standard (Landolt, ApJ, 1968).
s 1970+ WD pulsations explained by gravity modes driven by
mechanism in partial ionization H atmosphere.
Note: more common pressure modes have periods: ∼ seconds
2 / 28

8. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
3 / 28

9. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
3 / 28

10. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
s 1985 Period change due to secular cooling measured from multi-site
photometry on PG 1159 (Winget et al. 1985).
3 / 28

11. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
s 1985 Period change due to secular cooling measured from multi-site
photometry on PG 1159 (Winget et al. 1985).
s 1990 WET: the Whole Earth Telescope (Nather et al., ApJ 361)
3 / 28

12. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
s 1985 Period change due to secular cooling measured from multi-site
photometry on PG 1159 (Winget et al. 1985).
s 1990 WET: the Whole Earth Telescope (Nather et al., ApJ 361)
s 1991 WET observations of PG 1159−035 (Winget et al., ApJ 378)
3 / 28

13. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
s 1985 Period change due to secular cooling measured from multi-site
photometry on PG 1159 (Winget et al. 1985).
s 1990 WET: the Whole Earth Telescope (Nather et al., ApJ 361)
s 1991 WET observations of PG 1159−035 (Winget et al., ApJ 378)
s 1994 WET observations of GD 358 (Winget et al., ApJ 430)
3 / 28

14. WD History (continued)
s 1979 First DOV degenerate pulsator discovered (PG 1159−035).
(McGraw et al.) – explained by driving mechanism in partial ionized C
and O layers.
s 1982 First helium atmosphere WD pulsator discovered (GD 358),
following theoretical prediction of pulsation driving in He partial
ionization zone (Winget et al.)
s 1985 Period change due to secular cooling measured from multi-site
photometry on PG 1159 (Winget et al. 1985).
s 1990 WET: the Whole Earth Telescope (Nather et al., ApJ 361)
s 1991 WET observations of PG 1159−035 (Winget et al., ApJ 378)
s 1994 WET observations of GD 358 (Winget et al., ApJ 430)
s WET continues . . . . . .
3 / 28

15. WD relative size
4 / 28

16. Stellar structure equations
Mechanical structure - P (r), ρ(r), m(r)
r
dP Gm(r)
= −ρ(r)g(r) ; g(r) = ; m(r) = ρ(r)4πr2 dr
dr r2 0
Thermal structure - T (r), L(r), . . .
dT dL
= (· · · ) ; = (· · · )
dr dr
5 / 28

17. Common stellar P(r),ρ(r),T(r) profiles
6 / 28

18. WD Mechanical Structure
s WD support mechanism dominated by electron degeneracy pressure,
which is essentially independent of temperature −→ depends on density
7 / 28

19. WD Mechanical Structure
s WD support mechanism dominated by electron degeneracy pressure,
which is essentially independent of temperature −→ depends on density
s Hence in a WD, mechanical structure decoupled from thermal structure
7 / 28

20. WD Mechanical Structure
s WD support mechanism dominated by electron degeneracy pressure,
which is essentially independent of temperature −→ depends on density
s Hence in a WD, mechanical structure decoupled from thermal structure
s Nonrelativistic (NR) electron gas
3 1 5 5
n∝ pF ; P = vp −→ P ∝ PF −→ P ∝ ρ 3
3
s Extremely relativistic (ER) electron gas
1 4
n∝ p3
F ; 4
P = cp −→ P ∝ PF −→ P ∝ ρ 3
3
7 / 28

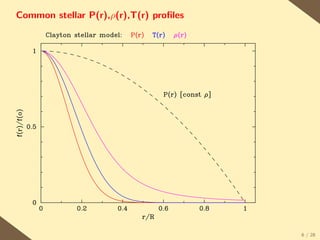
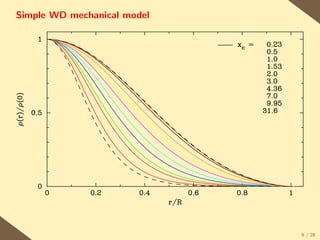
21. Simple WD mechanical model
The following relatively simple differential equation describing x(r)
(which is the electron momentum at the [local] fermi surface) quite accurately
characterises the density and pressure profiles of WDs.
3
d2 u 2 du 1 2
+ + u2 − 2 =0
dz 2 z dz xc + 1
where
1
x2 +1 2 pF (r)
u= and x=
x2 + 1
c me c
Solve numerically for x(r):
x(r) −→ ρ(r), P (r)
8 / 28

22. Simple WD mechanical model
9 / 28

23. Behaviour of increasingly relativistic particles
10 / 28

24. WD density & temperature profiles
11 / 28

25. WD Radius vs Mass
12 / 28

26. WD Radius vs Mass
13 / 28

27. White dwarf spectroscopy (Magellan 6.5m)
14 / 28

28. EC 20058 (He atm.) and flux standard (H atm.)
15 / 28

29. White dwarf time-series photometry
16 / 28

30. A WD light curve (MtJohn 1-m)
17 / 28

31. WD light curve (Magellan 6.5-m telescope (Chile)
18 / 28

32. Two different WD light curves
19 / 28

33. A white dwarf with nonsinusoidal pulse shapes
20 / 28

34. A white dwarf with nonsinusoidal pulse shapes
21 / 28

35. WET (mult-site) time-series light curves
22 / 28

36. WET xcov15 DFT, Sullivan et al., MNRAS (2008)
23 / 28

37. Nonradial pulsations: spherical harmonics
24 / 28

38. Asteroseismology and white dwarf physics
s Core chemical composition - stellar nuclear reaction ashes
dominated by 12 C and 16 O.
s Core crystallization
s Convection zone studies
s Neutrino cooling mechanism
25 / 28

39. White dwarf cooling models - neutrino cooling
26 / 28

40. Plasmon neutrino processes − Feynman diagrams
27 / 28

41. Neutrino physics in hot WD plasmas
s Basically, neutrinos produced by e− e+ annihilation
s But where do the positrons come from?
s Even at WD core temperatures, not enough energy for
real e− ,e+ pairs
s However, plenty of short duration (real) virtual e− ,e+ pairs created
courtesy energy-time uncertainty principle
s But, these pairs recombine with probability 0.99999 . . .
s However, this probability is not 1, and there is a ∼ 1 in 10−19 chance of
forming neutrino-antineutrino pairs via W± , Z0 exchange/creation
processes (the electroweak connection).
s Given the ν mass is ∼ zero, energy conservation permits formation of a
two ν final state from a ∼ KeV photon, but momentum conservation
requires more than a photon in initial state
s Possible other particles: nuclei, many particles −→ plasmons (this is the
dominant mechanism)
28 / 28