A simple presentation on N queen Algorithm. These slides dont have much information. You have to collect it by yourself. At the 8th slide, you will get the information from this link bellow. https://www.youtube.com/watch?v=xouin83ebxE&t=497s

1. 1

2. W E L C O M E !
Thank you for coming today!
2

3. MD. A.I.Tazib
ID: 153-15-6683

4. INTRODUCTION

5. 5
N Q u e e n
P r o b l e m
The N Queen is the problem of placing N
chess queens on an N×N chessboard so that
no two queens attack each other.
For example, following is a solution for 4
Queen problem.

6. Solutions

7. V a r i o u s a p p r o a c h e s :
7
Brute force
Backtracking
Permutation
generation
Graph theory
concepts
Divide and conquer
approach
Mathematical
solutions

8. Backtracking Solution :
0
1
2
3
0 1 2 3
0
1
2
3
Positions:

9. 9
F i n a l
S o l u t i o n
Q
Q
Q
Q

10. Bac k trac k ing
Algorithm

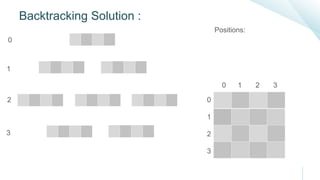
11. Backtracking Algorithm :
1) Start from the left most column.
2) If all Queens are placed
return true.
3) Try all rows in the current column. Do following for every tried row.
a) If the queen can be placed safely in this row then mark this [row,
column] as part of the solution and recursively check if placing
queen here leads to a solution.
b) If placing queen in [row, column] leads to a solution then return
true.
c) If placing queen doesn't lead to a solution then unmark this [row,
column] (Backtrack) and go to step (a) to try other rows.
4) If all rows have been tried and nothing worked, return false to trigger
backtracking.

12. T H A N K Y O U !
A N Y Q U E S T I O N S ?