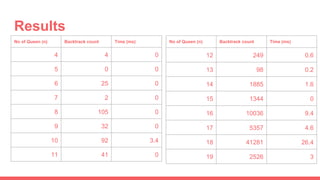
The document discusses the N-Queen puzzle problem of placing N chess queens on an N×N board so that no two queens attack each other. It presents a backtracking algorithm to solve the problem by placing queens one by one on each row from left to right while checking that the queen does not attack other previously placed queens. The algorithm tracks the number of backtracks required to solve instances of different board sizes (N) and the time taken. Solutions for boards up to size 30 are presented along with analysis of results and references for more information.

1. N-Queen
Puzzle
Akash Sethiya
Mississippi State University
Computer Science Graduate

2. Overview
The N queen puzzle is the problem of placing N chess queens on an NxN chess board
so that no two queens attack each other.
A queen can attack to another queen only if both queens shares same row, or
column, or diagonal.

3. Solution Algorithm
This problem can be solved by Backtracking and “branch and bound”.
Using Backtracking approach:
First we place the first queen on the first row first column of the chess board.
Then from second row placing second queen only if it passed three validation such
as : second queen is not on the same row or same column of the first queen, also
it does not lie on the diagonal of the first queen.
If the column comes to end and no solution found, we backtrack to previous row
and repeat the algorithm.
And if all the rows and columns comes to end and no solution found then we can

4. Algorithm Pseudo code
nQueen(row,n)
for(i=1 to n)
if(isPositionValidForQueen(row,i)) //check weather the cell is valid for queen or
not
board[row][i] = 1; // Place a queen;
if(row == n)
//done - return true;
else
nQueen(row+1,n)
board[row][i]=0; //backtrack
return false;

5. Results
No of Queen (n) Backtrack count Time (ms)
4 4 0
5 0 0
6 25 0
7 2 0
8 105 0
9 32 0
10 92 3.4
11 41 0
No of Queen (n) Backtrack count Time (ms)
12 249 0.6
13 98 0.2
14 1885 1.6
15 1344 0
16 10036 9.4
17 5357 4.6
18 41281 26.4
19 2526 3

6. Results
No of Queen (n) Backtrack count Time (ms)
20 199615 131
21 8541 6.4
22 1737166 928.4
23 25405 13.8
24 411584 223.6
25 48658 26.4
26 397673 234.4
27 454186 274.2
No of Queen (n) Backtrack count Time (ms)
28 3006270 1894.2
29 1532210 1002.4
30 56429589 38565.6

7. Result Analysis

8. Alternate Approach - Without Backtracking
Success
(Stop)

9. References
https://www.youtube.com/watch?v=kX5frmc6B7c&t=444s
http://www.geeksforgeeks.org/backtracking-set-3-n-queen-problem/
https://en.wikipedia.org/wiki/Eight_queens_puzzle

10. Thank you
Akash Sethiya