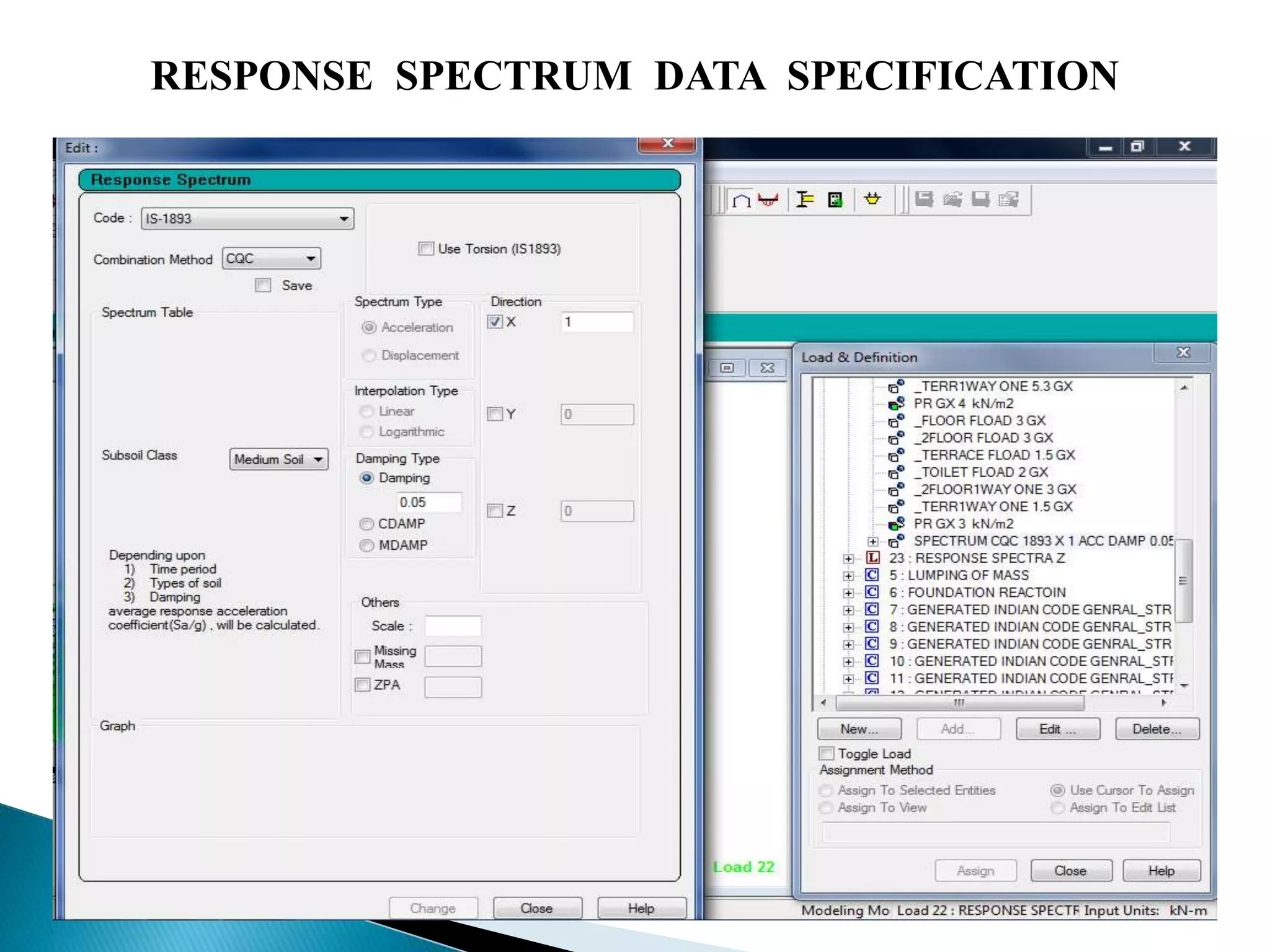
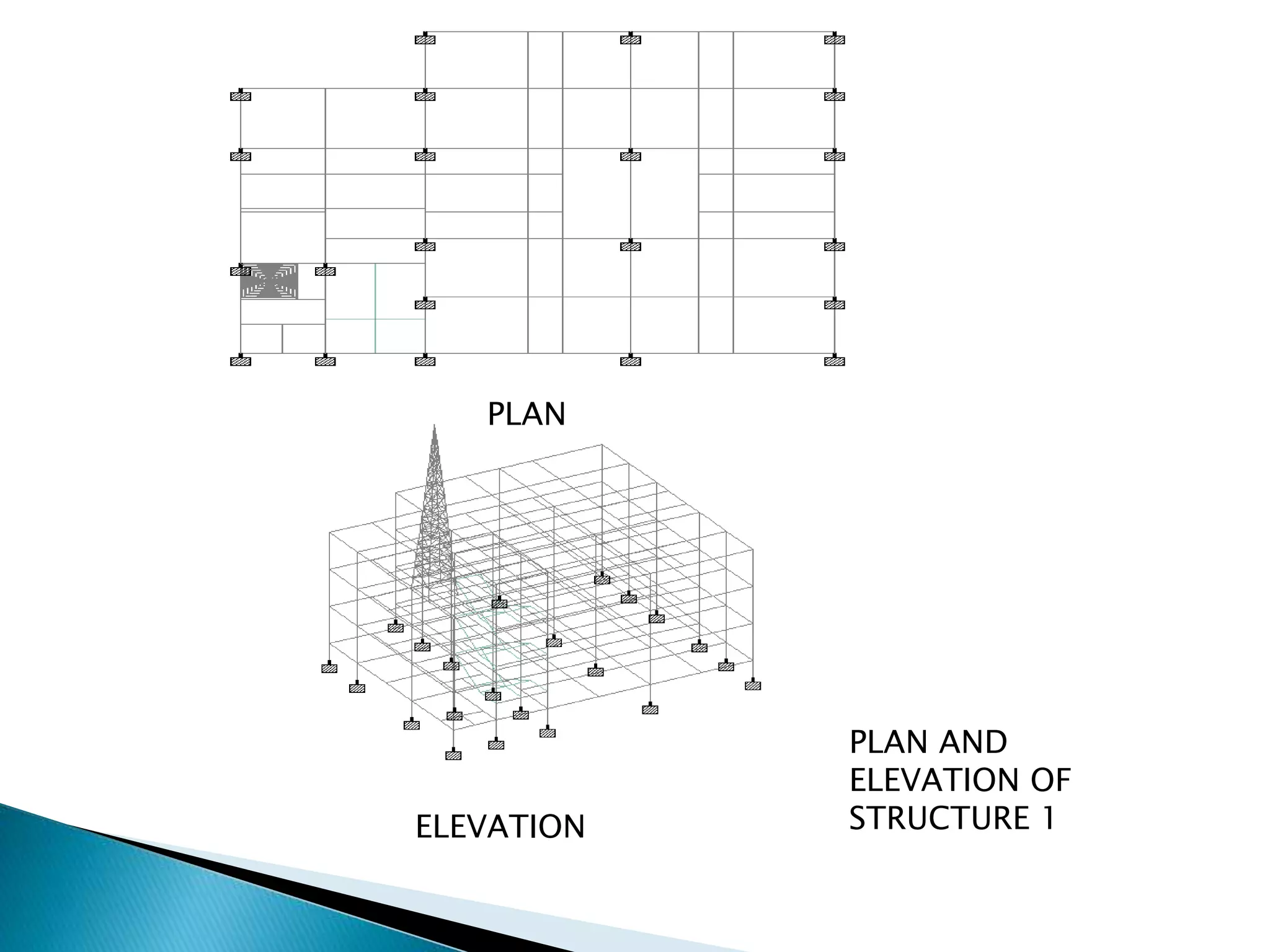
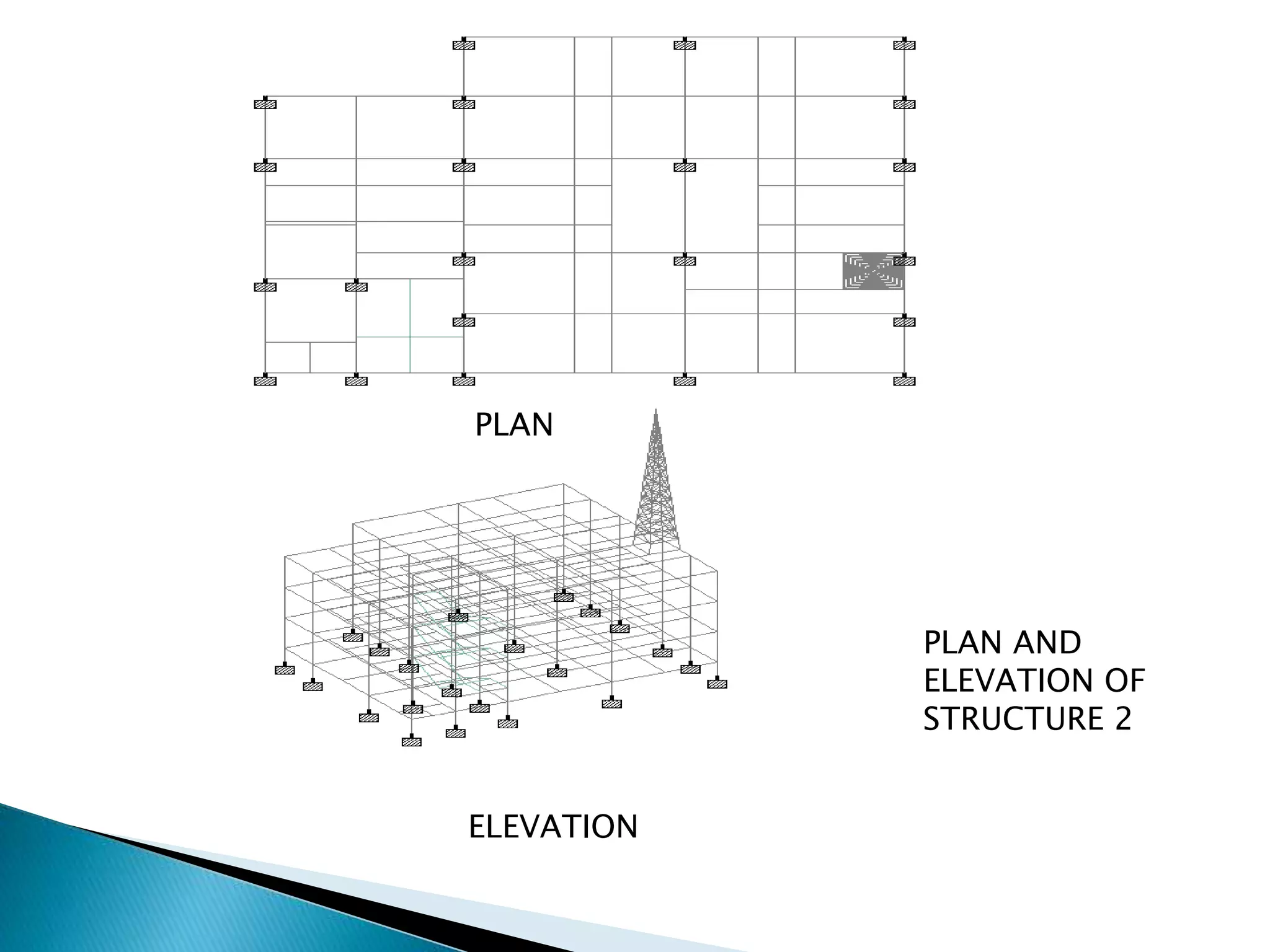
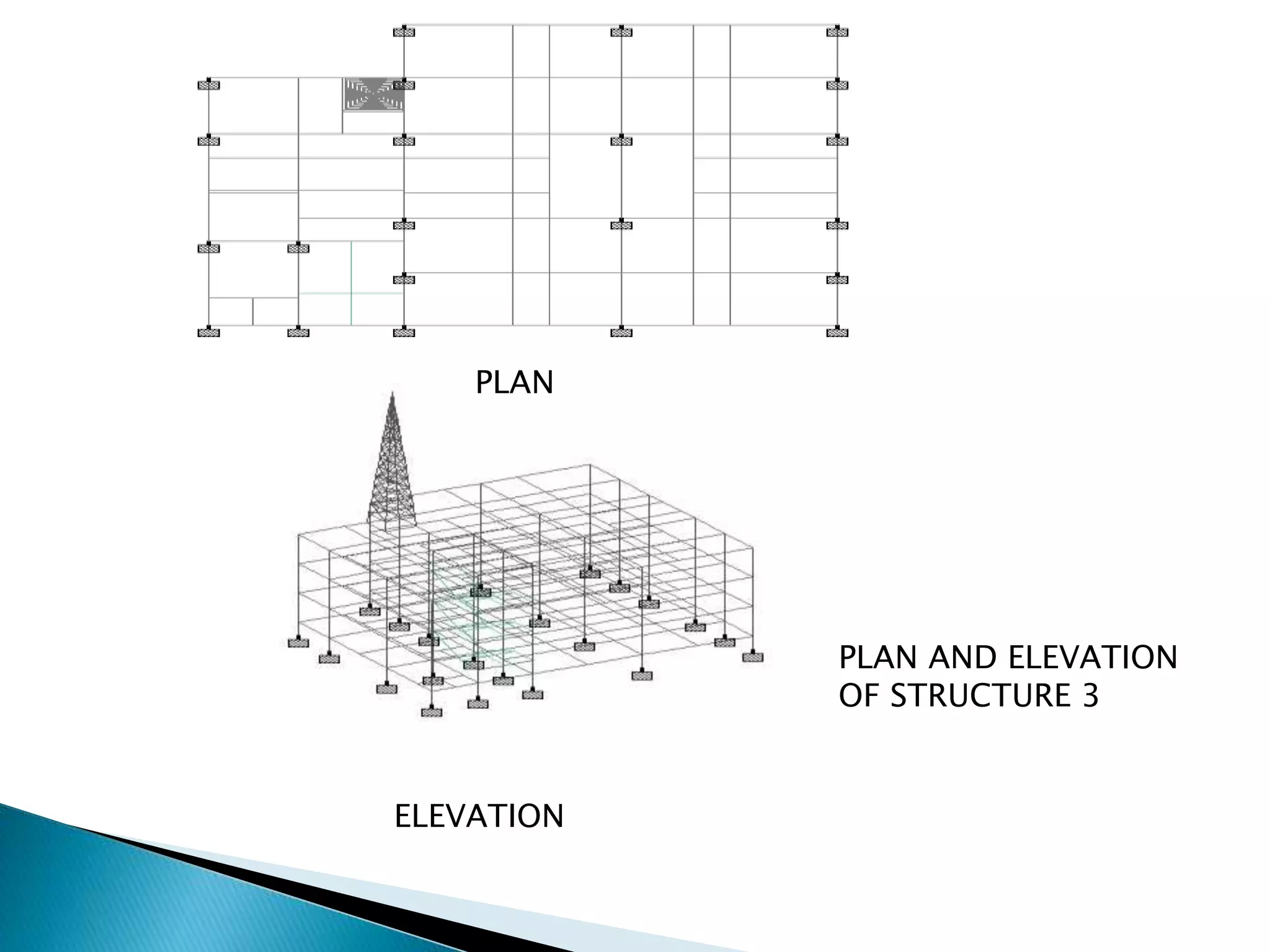
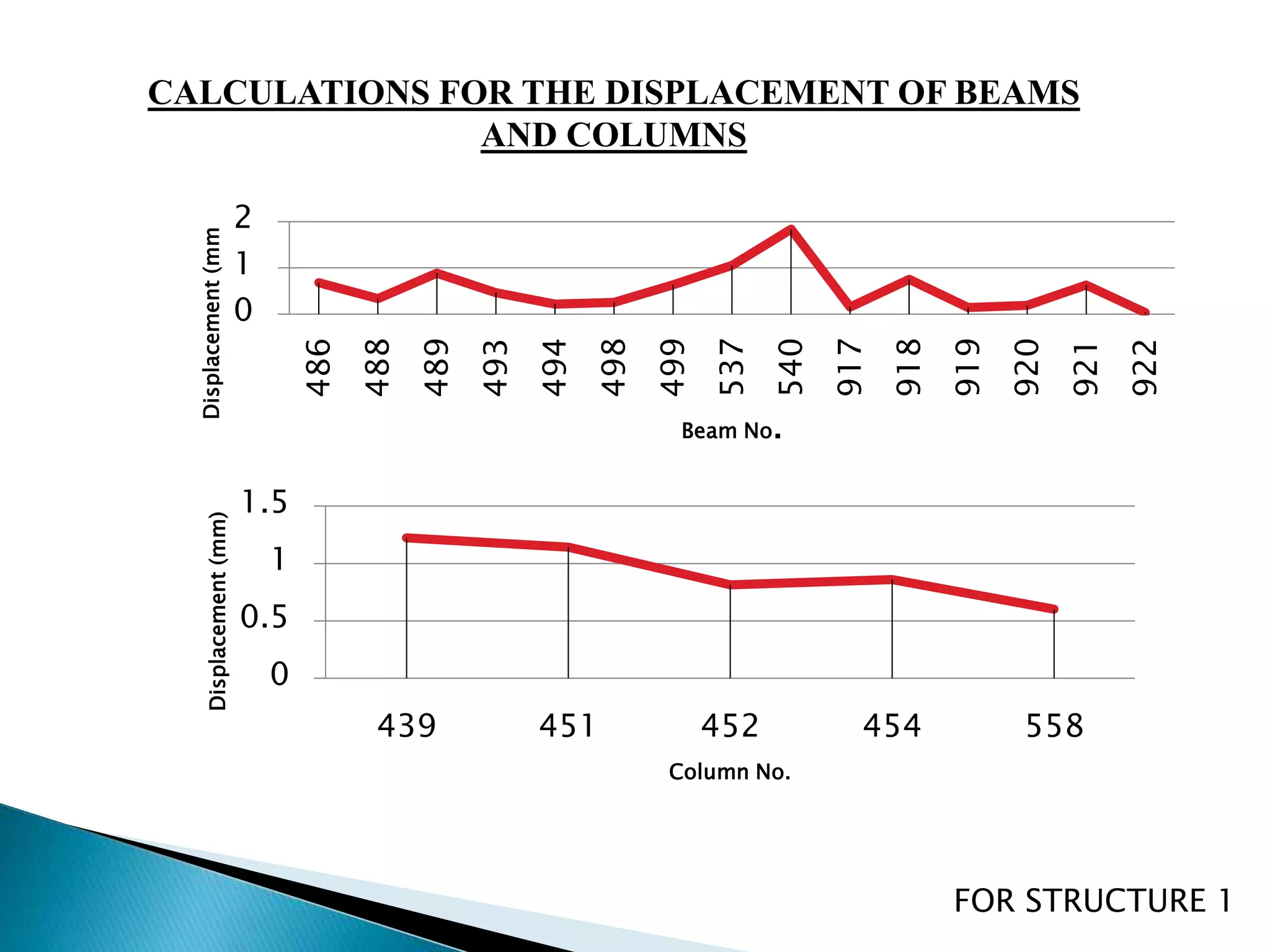
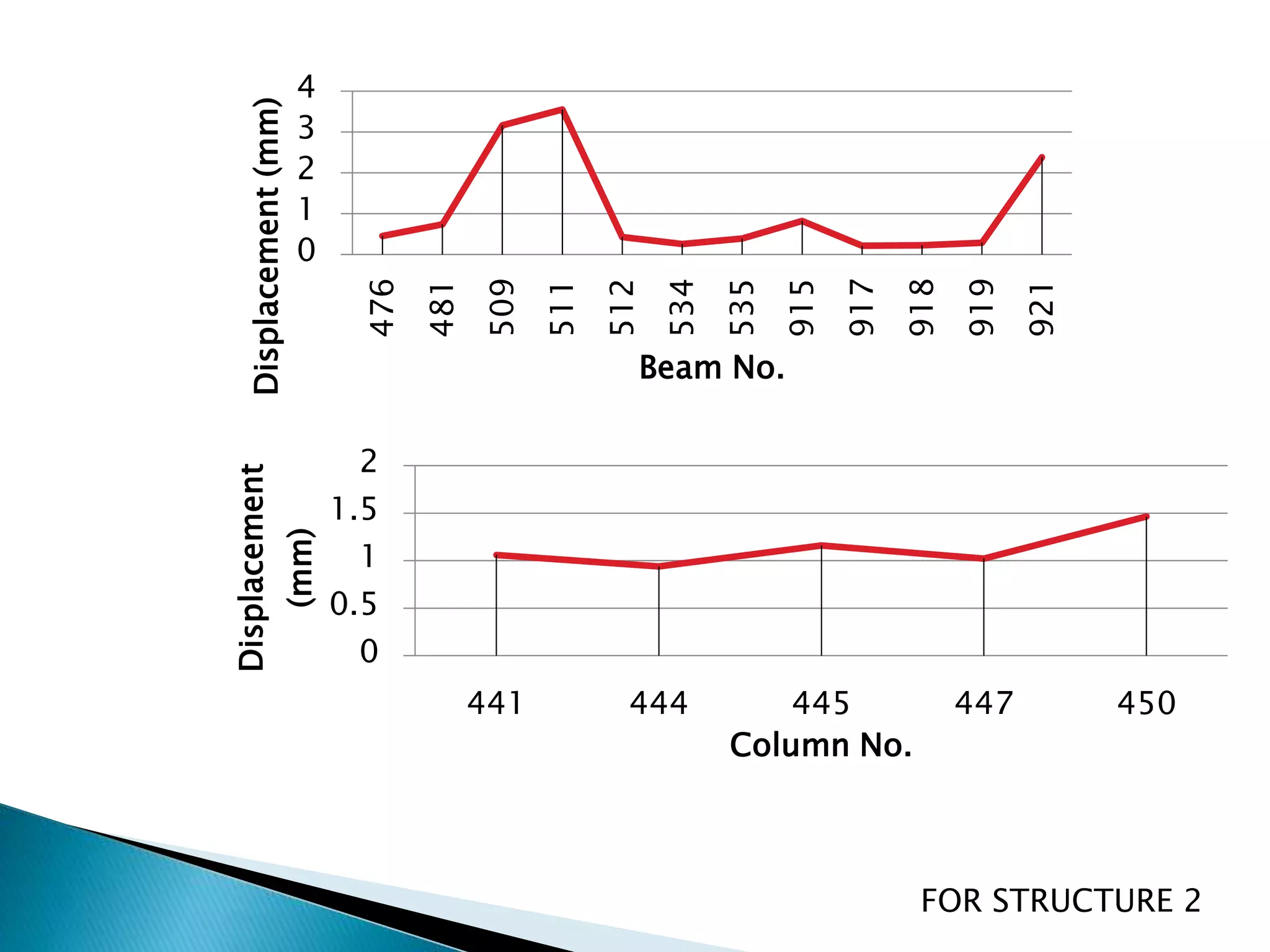
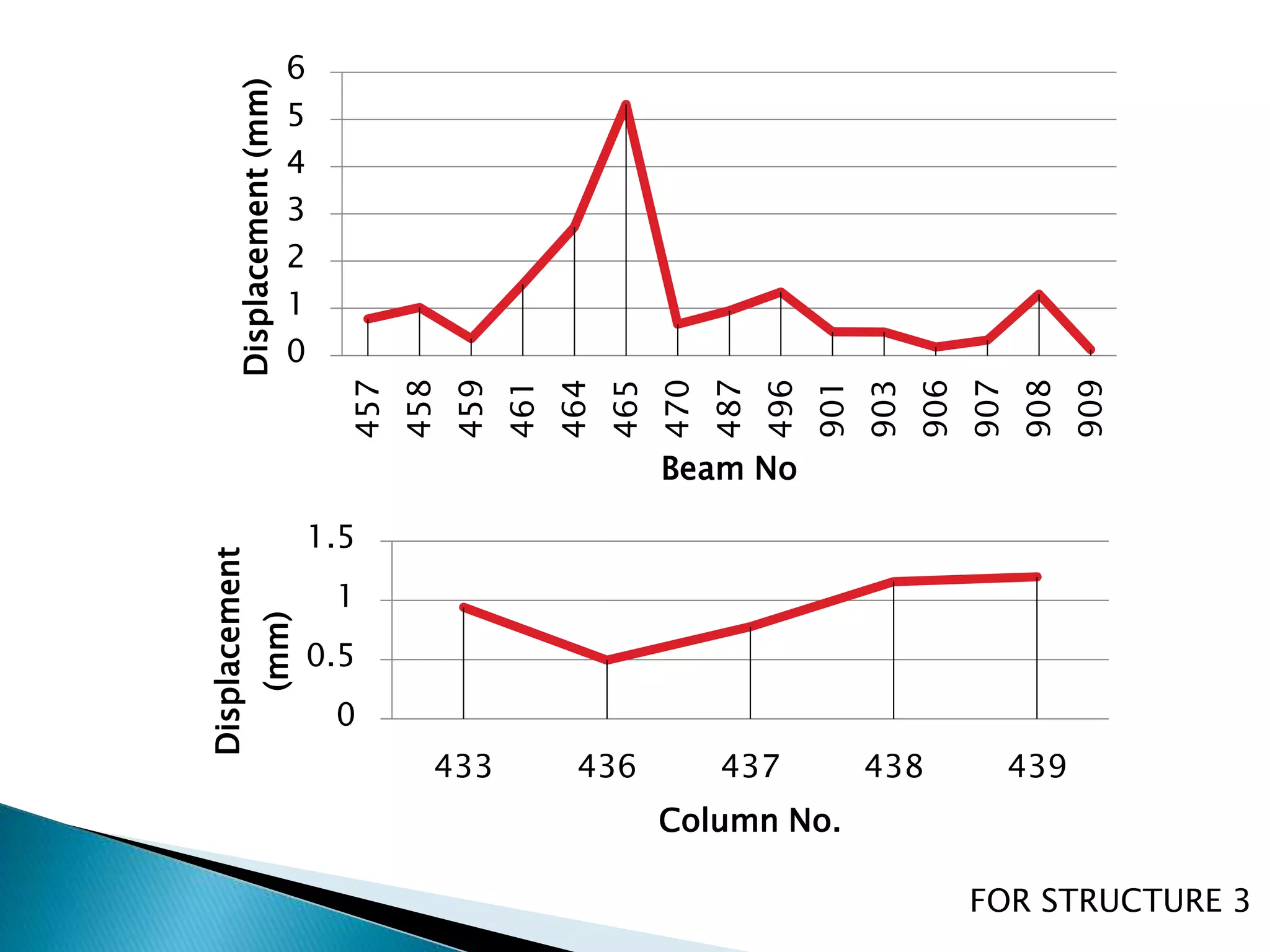
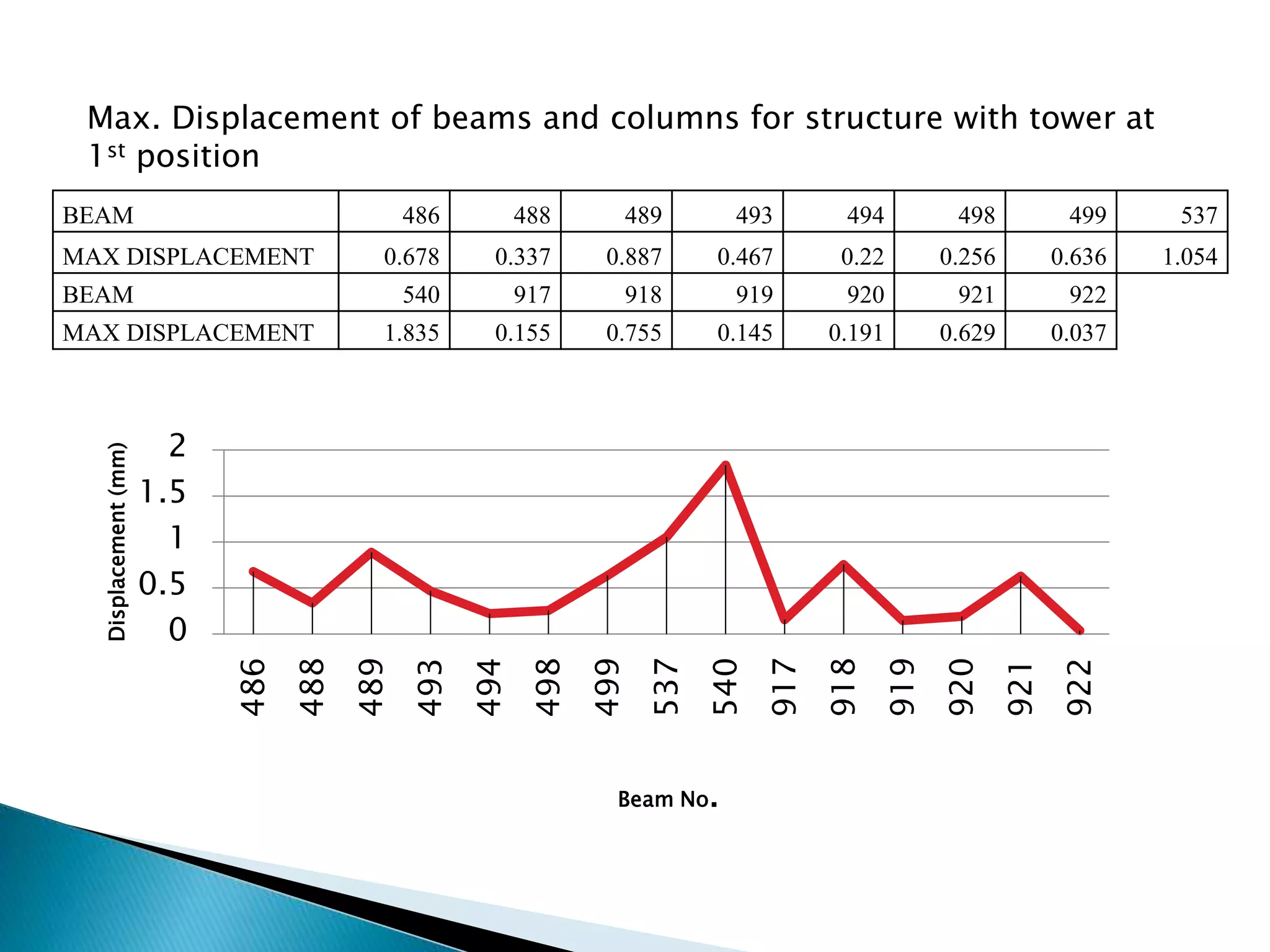
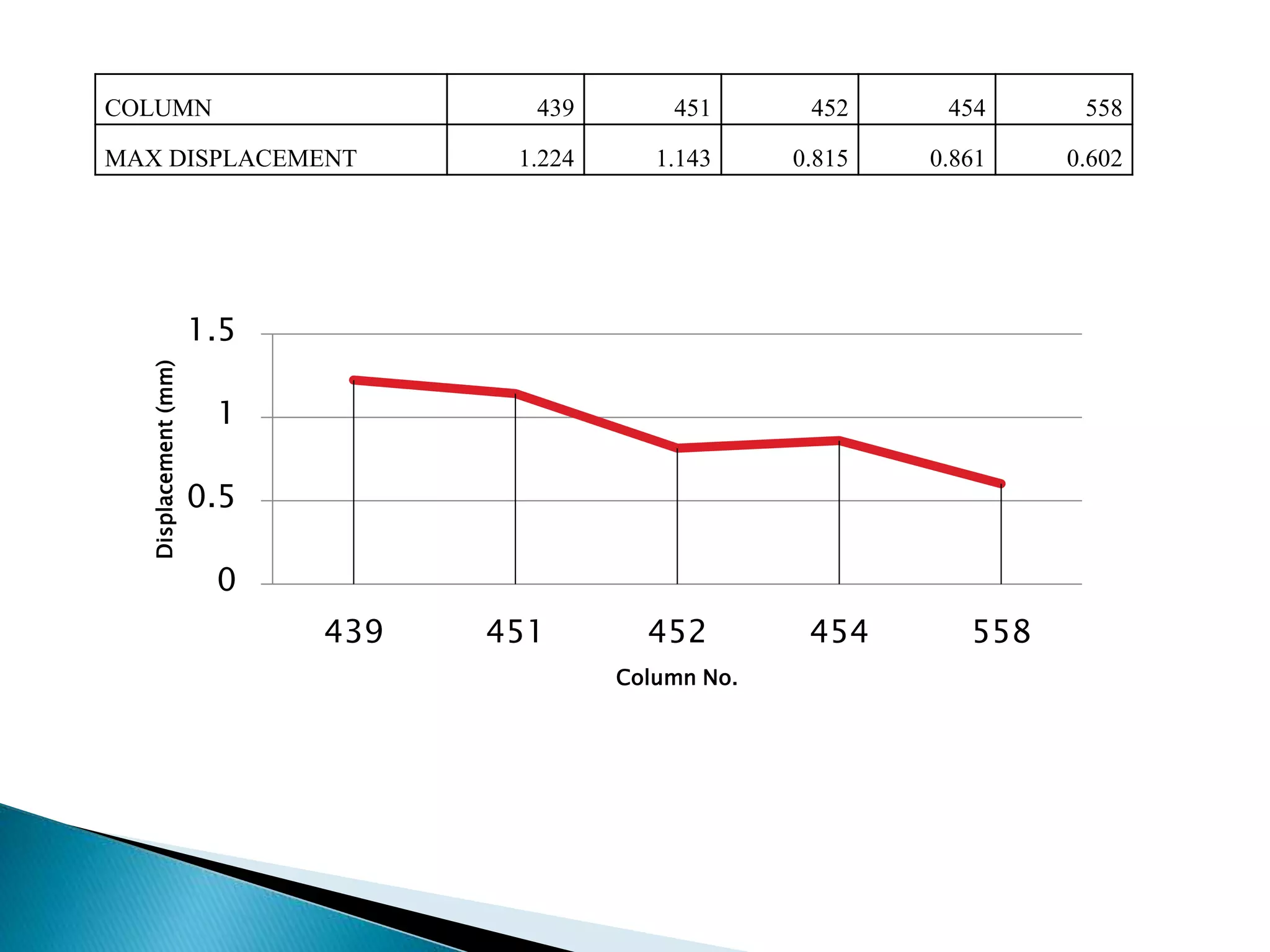
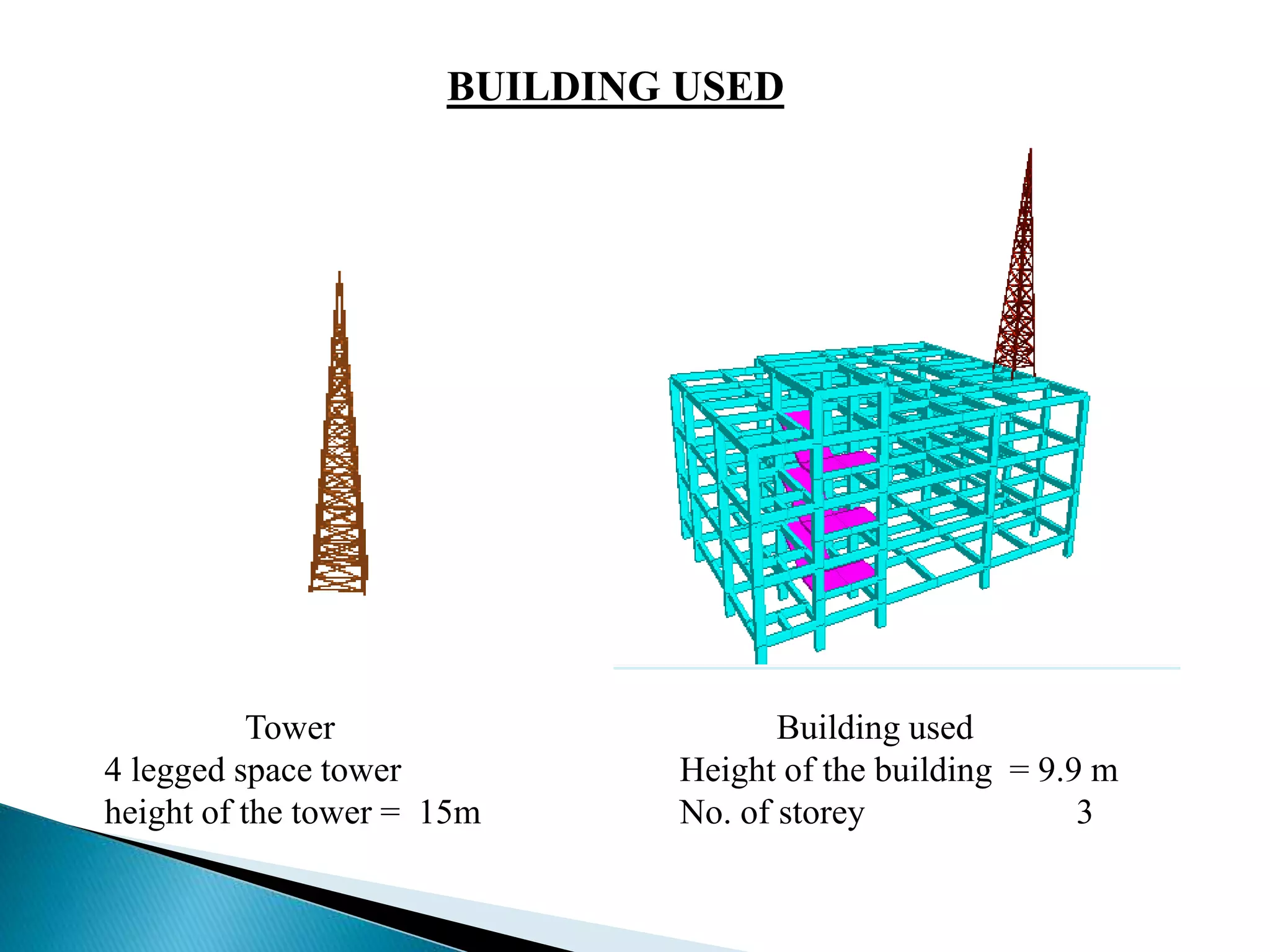
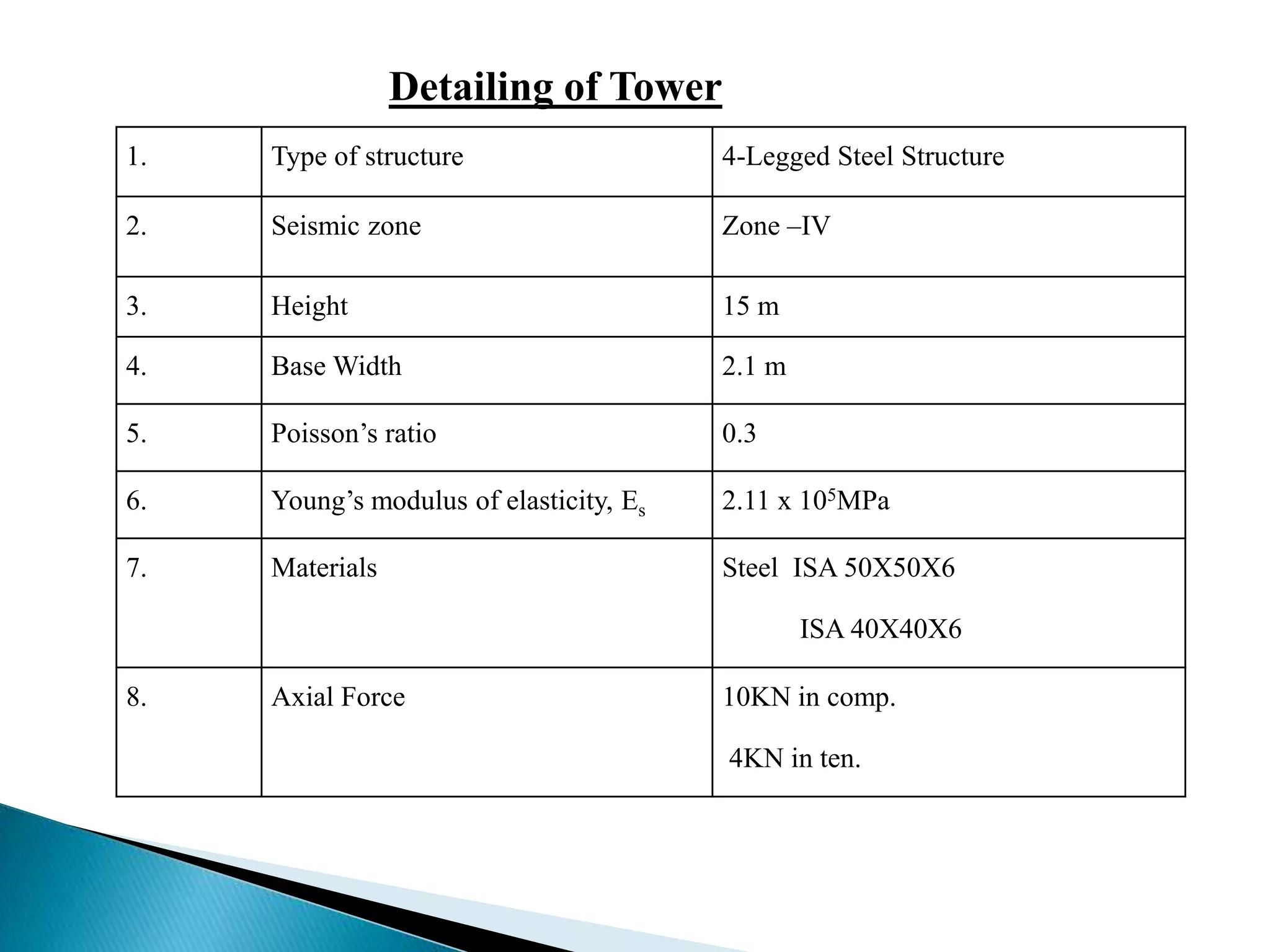
This document summarizes the dynamic analysis of a multi-storey framed structure with a roof tower conducted using STAAD-Pro. The objectives were to model the tower and building, study their response using the response spectra method under seismic loading, and analyze wind loads. A 3-storey building with dimensions and material properties was modeled along with a 15m 4-legged steel tower. Load combinations, mode shapes, and response spectra were defined to obtain displacements of beams and columns for the three structures under different load cases. Structure 2 and 3 showed higher displacements than Structure 1. Wind loads were not considered as the building height was under 10m.

1. DYNAMIC ANALYSIS
OF
MULTISTOREY FRAMED STRUCTURE
WITH ROOF TOWER
Guide :- Mr. PRAMOD TIWARI
PRESENTED BY:
Amit Ranjan (2002309)
Gupta Abhishek (2002964)
Mohit Jain (2002355)
Navdeep Kumar (2002357)
Siddhant Raturi (2002403)
Vipin Thapliyal (2002854)

2. INTRODUCTION
• Telecommunication structure designed for supporting
parabolic antennas.
e.g. microwave transmission for communication , radio and
T.V signals.
• Self-supporting structures.
• Three-legged and Four-legged space trussed structures.
• Consideration of load.
 Seismic load.
 Wind load.

3. OBJECTIVES
 Modeling of the tower.
 Modeling of the building.
 Study of the Response Spectra Method on the building with roof tower.
 Study of the wind load on the building.

4. BUILDING USED
Building used
Height of the building = 9.9 m
No. of storey 3
Tower
4 legged space tower
height of the tower = 15m

5. Detailing of Building
1. Type of structure Multi-storey rigid jointed framed structure
2. Seismic zone Zone -IV
3. Number of stories Three ( G+2 )
4. Floor height 3.3 m
5. Infill wall 250 mm thick including plaster in longitudinal and 150 mm in
transverse direction
6. Imposed load 3 kN/m2
7. Materials Concrete ( M 25) and reinforcement (Fe 500)
8.
Size of columns
460 mm x 340 mm
530 mm x 340 mm
450 mm x 340 mm
9. Size of beams 450 mm x 230 mm
300 mm x 230 mm
10. Depth of slab 150 mm thick
11. Specific weight of RCC 24 kN/m3
12. Specific weight of infill 20 kN/m3
13. Type of soil Medium soil
14. Response spectra As per IS 1893 ( part 1): 2002
15. Time history Compatible to IS 1893 ( part 1): 2002 spectra at medium soil
for 5% damping.

6. 1. Type of structure 4-Legged Steel Structure
2. Seismic zone Zone –IV
3. Height 15 m
4. BaseWidth 2.1 m
5. Poisson’s ratio 0.3
6. Young’s modulus of elasticity, Es 2.11 x 105MPa
7. Materials Steel ISA 50X50X6
ISA 40X40X6
8. Axial Force 10KN in comp.
4KN in ten.
Detailing of Tower

7. STEPS INVOLVED IN WORKING OF STAAD- PRO
GEOMETRY
GENERAL
PROPERTY SUPPORTS LOAD & DEFINITION
CROSS
SECTION
FIXED AND
PINNED
DEFINITION
DYNAMIC LOAD
RESPONSE SPECTRA
METHOD
LOAD CASE &
DETAILS
ANALYSE

8. RESPONSE SPECTRA
 Response spectra is a very useful tool of earthquake engineering
for analysing the performance of structure during earthquake.
 Response spectra is simply a plot of the peak or steady state
response (disp., vel., ace.)
 Response spectra is measured using accelerograph.

9. RESPONSE SPECTRUM METHOD BY USING
STAADPRO
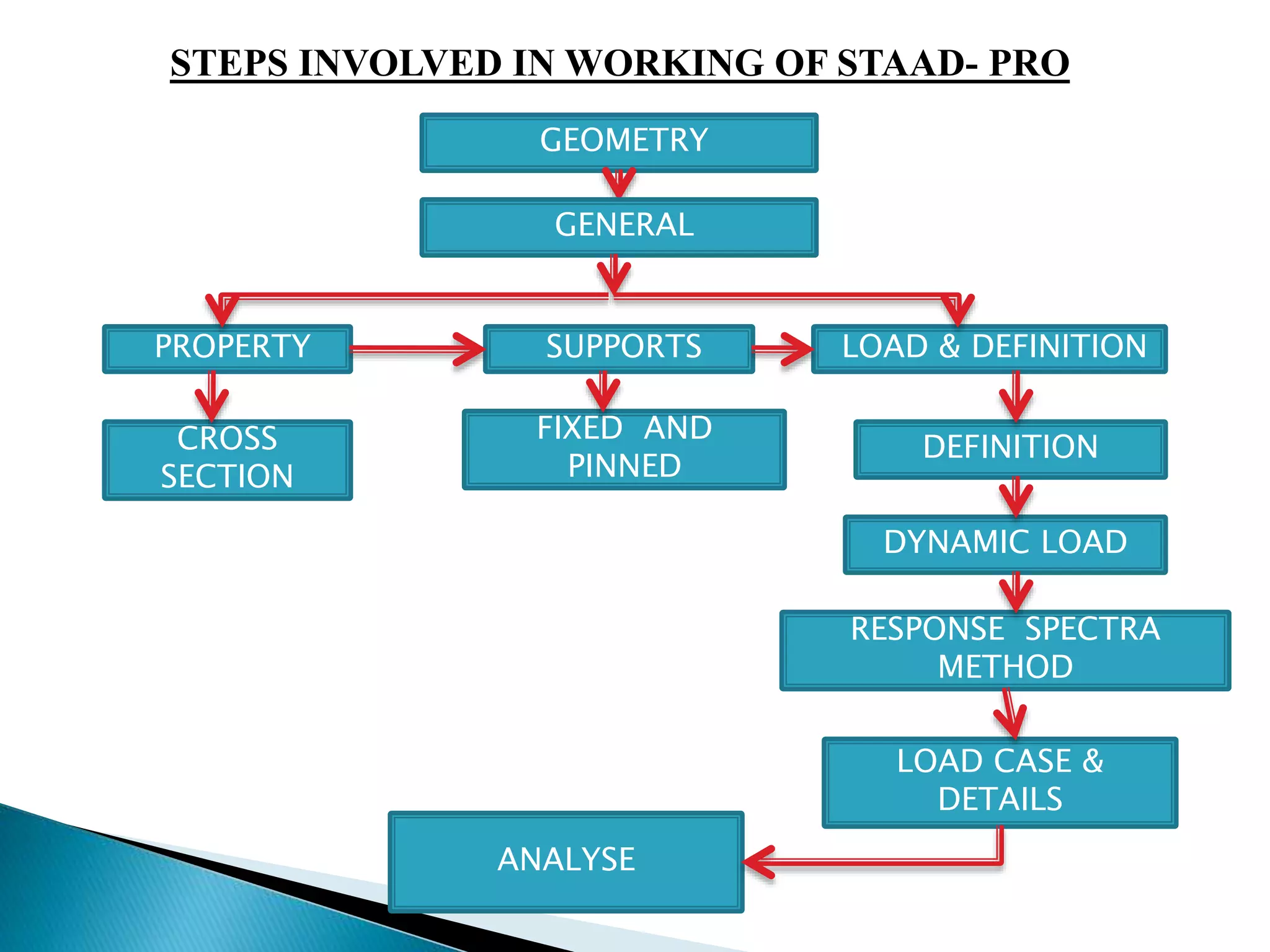
The design lateral shear force at each floor in each mode is
computed by STAAD in accordance with the IS: 1893 (Part 1) -
2002
STAAD utilizes the following procedure to generate the lateral seismic
loads.
[1] User provides the value for as factors for input spectrum. I* Z / 2 R
[2] Program calculates time periods for first six modes or as specified
by the user.
[3] Program calculates Sa/g for each mode utilizing time period and
damping for each mode.

10. [4] The program calculates design horizontal acceleration spectrum
for different modes
[5] The program then calculates mode participation factor for different
modes.
[6] The peak lateral seismic force at each floor in each mode is
calculated.
[7] All response quantities for each mode are calculated.
[8] The peak response quantities are then combined as per method
(CQC or SRSS or ABS ) as defined by the user to get the final results

11. RESPONSE SPECTRUM DATA SPECIFICATION

12. Mode shape
Mode shape is the deformed shape of the building when
shaken at natural period
Factors influencing Mode Shapes
(1) Effect of Flexural Stiffness of Structural Elements
(2) Effect of Axial Stiffness of Vertical Members
(3) Effect of Degree of Fixity at Member Ends
(4) Effect of Building Height

13. Wind :
Wind is the term used for air in motion and
is usually applied to the natural horizontal
motion of the atmosphere.
Types of wind:
1. Prevailing wind
2. Seasonal wind
3. Local wind

14. Design analysis of wind :
Design Wind Speed (Vz) :
Vz = Vb k1 k2 k3
Vz = design wind speed at any height z in m/s,
k1 = probability factor (risk coefficient)
k2 = terrain roughness and height factor
k3 = topography factor
Design Wind Pressure (pz):
pz = 0.6 vz
2
pz = wind pressure in N/m2 at height z, and
Vz = design wind speed in m/s at height z.

15. LOAD COMBINATIONS CONSIDERED IN
THIS ANALYSIS ARE
1) 1.5(DL+LL)
2) 1.2(DL+LL)
3) 1.2(DL+LL+EQX)
4) 1.2(DL+LL-EQX)
5) 1.2(DL+LL+EQZ)
6) 1.2(DL+LL-EQZ)
7) 1.5DL
8) 1.5(DL+EQX)
9) 1.5(DL+EQZ)
10) 1.5(DL-EQX)
11) 1.5(DL-EQZ)
12) 0.9DL+1.5EQX
13) 0.9DL+1.5EQZ
14) 0.9DL-1.5EQX
15) 0.9DL-1.5EQZ

16. PLAN
ELEVATION
PLAN AND
ELEVATION OF
STRUCTURE 1

17. PLAN
ELEVATION
PLAN AND
ELEVATION OF
STRUCTURE 2

18. PLAN
ELEVATION
PLAN AND ELEVATION
OF STRUCTURE 3

19. CALCULATIONS FOR THE DISPLACEMENT OF BEAMS
2
1
0
AND COLUMNS
486
488
489
493
494
498
499
537
540
917
918
919
920
921
922
Displacement (mm
Beam No.
1.5
1
0.5
0
439 451 452 454 558
Displacement (mm)
Column No.
FOR STRUCTURE 1

20. 4
3
2
1
0
476
481
509
511
512
534
535
915
917
918
919
921
Displacement (mm)
Beam No.
2
1.5
1
0.5
0
441 444 445 447 450
Displacement
(mm)
Column No.
FOR STRUCTURE 2

21. 6
5
4
3
2
1
0
457
458
459
461
464
465
470
487
496
901
903
906
907
908
909
Displacement (mm)
Beam No
1.5
1
0.5
0
433 436 437 438 439
Displacement
(mm)
Column No.
FOR STRUCTURE 3

22. RESULT AND CONCLUSION
1. The displacement of structure 2 and 3 are more than that of structure 1 by
comparing their graphical values which are generated with the help of software.
2. As the height of the building is 9.9 m and according to IS code the wind load is
applied on the structures whose height is more than 10 m ,So there is no need of
applying wind load.

23. Max. Displacement of beams and columns for structure with tower at
1st position
BEAM 486 488 489 493 494 498 499 537
MAX DISPLACEMENT 0.678 0.337 0.887 0.467 0.22 0.256 0.636 1.054
BEAM 540 917 918 919 920 921 922
MAX DISPLACEMENT 1.835 0.155 0.755 0.145 0.191 0.629 0.037
2
1.5
1
0.5
0
486
488
489
493
494
498
499
537
540
917
918
919
920
921
922
Displacement (mm)
Beam No.

24. COLUMN 439 451 452 454 558
MAX DISPLACEMENT 1.224 1.143 0.815 0.861 0.602
1.5
1
0.5
0
439 451 452 454 558
Displacement (mm)
Column No.

25. REFERENCES
 IS - 1893 – 2002 (part - 1)
 IS - 875 (part - 3)
Bhosale N.Kumar P., Pandey A.D., (2012), Influence of Host Structure
Characteristics on Response of Rooftop Telecommunication Towers,
International Journal of Civil and Structural Engineering, 2(3), 2012.
 Siddhesha H., (2010), Wind analysis of Microwave Towers, International
Journal of Applied Engineering Research, Dindigul, 1(3), 574-584.
 Amiri G., Barkhordari M.A., Massah S. R., Vafaei M.R.,(2007), Earthquake
Amplification Factors for Self-supporting 4-legged Telecommunication
Towers, World Applied Sciences Journal, 6(2), 635-643.
 McClure G., Georgi L., Assi R, (2004), Seismic considerations for
telecommunication towers mounted on building rooftop, 13th World
Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 1988.