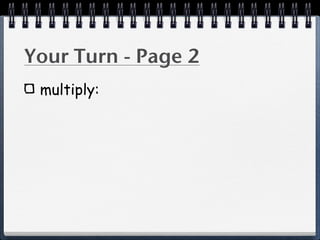
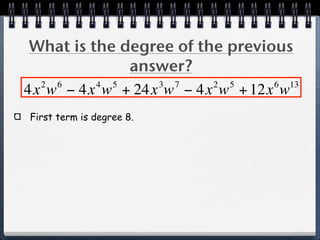
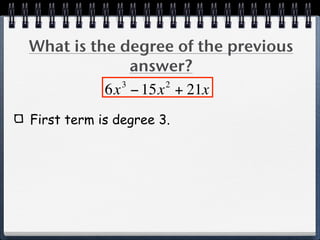
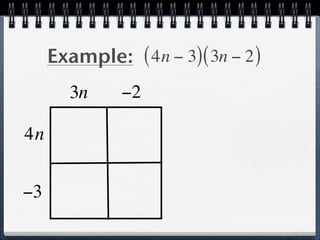
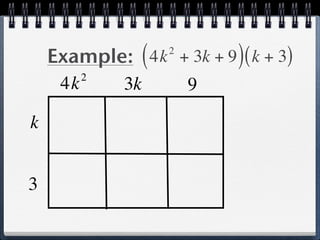
The document discusses multiplying polynomials by monomials. It provides examples of multiplying terms inside parentheses by a monomial outside, including distributing the monomial to each term. The key steps are to distribute the monomial to each term and then multiply the coefficients and variables. The degree of the resulting polynomial is determined by the highest exponent of any term.

1. Multiplying
Polynomials

2. Multiply a Polynomial by a
Monomial
Multiply each term
inside the parenthesis
2
( 2
3x 2x − 7x + 5 )
by the monomial
outside the
parenthesis.
The number of terms
inside the parenthesis
will be the same as
after multiplying.

3. Multiply a Polynomial by a
Monomial
Multiply each term
inside the parenthesis
2
(
3x 2x − 7x + 52
)
by the monomial
outside the
3x 2
( 2x ) + 3x ( −7x ) + 3x ( 5 )
2 2 2
parenthesis.
The number of terms
inside the parenthesis
will be the same as
after multiplying.

4. Multiply a Polynomial by a
Monomial
Multiply each term
inside the parenthesis
2
(
3x 2x − 7x + 52
)
by the monomial
outside the
3x 2
( 2x ) + 3x ( −7x ) + 3x ( 5 )
2 2 2
parenthesis.
The number of terms
inside the parenthesis
will be the same as
after multiplying.

5. Multiply a Polynomial by a
Monomial
Multiply each term
inside the parenthesis
2
(
3x 2x − 7x + 52
)
by the monomial
outside the
3x 2
( 2x ) + 3x ( −7x ) + 3x ( 5 )
2 2 2
parenthesis.
The number of terms
inside the parenthesis
2
(
3x 2x − 7x + 5 2
)
will be the same as
after multiplying.

6. Multiply a Polynomial by a
Monomial
Multiply each term
inside the parenthesis
2
(
3x 2x − 7x + 52
)
by the monomial
outside the
3x 2
( 2x ) + 3x ( −7x ) + 3x ( 5 )
2 2 2
parenthesis.
The number of terms
inside the parenthesis
2
(
3x 2x − 7x + 5 2
)
will be the same as 4
6x − 21x + 15x 3 2
after multiplying.

7. Multiply a Polynomial by a
Monomial
Review this Cool Math site to learn about
multiplying a polynomial by a monomial.
Do the Try It and Your Turn problems in
your notebook and check your answers on
the next slides.

8. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 3 2
)

9. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 32
)
Distribute the monomial.

10. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 3 2
)
Distribute the monomial.
4 2 4
6x ⋅ 2x + 6x ⋅ 3

11. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 3 2
)
Distribute the monomial.
4 2 4
6x ⋅ 2x + 6x ⋅ 3
Multiply each term.

12. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 3 2
)
Distribute the monomial.
4 2 4
6x ⋅ 2x + 6x ⋅ 3
Multiply each term.
6 4
12x + 18x

13. Cool Math Try It - Page 1
Multiply: 4
(
6x 2x + 3 2
)
Distribute the monomial.
4 2 4
6x ⋅ 2x + 6x ⋅ 3
Multiply each term.
6 4
12x + 18x
Verify that your answer has same number of
terms as inside original ( ). Both have 2 terms.

14. What is the degree of the previous
answer?
6 4
12x + 18x

15. What is the degree of the previous
answer?
6 4
12x + 18x
First term is degree 6.

16. What is the degree of the previous
answer?
6 4
12x + 18x
First term is degree 6.
Second term is degree 4.

17. What is the degree of the previous
answer?
6 4
12x + 18x
First term is degree 6.
Second term is degree 4.
Therefore, the polynomial is degree 6.

18. Your Turn - Page 2
multiply:

19. Your Turn - Page 2
multiply:
3
( 5 2
10x 2x + 1 − 3x + x )

20. Your Turn - Page 2
multiply:
3
( 5 2
10x 2x + 1 − 3x + x )
Distribute the monomial.

21. Your Turn - Page 2
multiply:
3
(
10x 2x + 1 − 3x + x5 2
)
Distribute the monomial.
( )
10x 2x + 10x (1) + 10x −3x + 10x ( x )
3 5 3 3
( 2
) 3

22. Your Turn - Page 2
multiply:
3
(
10x 2x + 1 − 3x + x5 2
)
( )
10x 2x + 10x (1) + 10x −3x + 10x ( x )
3 5 3 3
( 2
) 3
Multiply each term.

23. Your Turn - Page 2
multiply:
3
(
10x 2x + 1 − 3x + x 5 2
)
( )
10x 2x + 10x (1) + 10x −3x + 10x ( x )
3 5 3 3
( 2
) 3
Multiply each term. 8 3 5 4
20x + 10x − 30x + 10x

24. Your Turn - Page 2
multiply:
3
(
10x 2x + 1 − 3x + x 5 2
)
( )
10x 2x + 10x (1) + 10x −3x + 10x ( x )
3 5 3 3
( 2
) 3
8 3 5 4
Put in descending 20x + 10x − 30x + 10x
order and verify
number of terms.
(Both have 4 terms.)

25. Your Turn - Page 2
multiply:
3
(
10x 2x + 1 − 3x + x 5 2
)
( )
10x 2x + 10x (1) + 10x −3x + 10x ( x )
3 5 3 3
( 2
) 3
8 3 5 4
Put in descending 20x + 10x − 30x + 10x
order and verify
number of terms. 8 5 4 3
(Both have 4 terms.)
20x − 30x + 10x + 10x

26. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x

27. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x
First term is degree 8.

28. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x
First term is degree 8.
Second term is degree 5.

29. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x
First term is degree 8.
Second term is degree 5.
Third term is degree 4.

30. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x
First term is degree 8.
Second term is degree 5.
Third term is degree 4.
Fourth term is degree 3.

31. What is the degree of the previous
answer?
8 5 4 3
20x − 30x + 10x + 10x
First term is degree 8.
Second term is degree 5.
Third term is degree 4.
Fourth term is degree 3.
Therefore, the polynomial is degree 8.

32. Try It - Page 2
Multiply:
2 5
( 2 2 4
4x w w − x + 6xw − 1 + 3x w 8
)

33. Try It - Page 2
Multiply:
2 5
( 2 2 4
4x w w − x + 6xw − 1 + 3x w 8
)
Distribute the monomial.

34. Try It - Page 2
Multiply:
2 5
(
4x w w − x + 6xw − 1 + 3x w 2 2 4 8
)
Distribute the monomial.
5
( 2
) 2 5
( 2
)
4x w ( w ) + 4x w −x + 4x w 6xw + 4x w ( −1) + 4x w 3x w
2 5 2 2 5 2 5
( 4 8
)

35. Try It - Page 2
Multiply:
2 5
(
4x w w − x + 6xw − 1 + 3x w 2 2 4 8
)
5
( 2
) 2 5
( 2
)
4x w ( w ) + 4x w −x + 4x w 6xw + 4x w ( −1) + 4x w 3x w
2 5 2 2 5 2 5
( 4 8
)
Multiply each term.

36. Try It - Page 2
Multiply:
2 5
(
4x w w − x + 6xw − 1 + 3x w 2 2 4 8
)
5
( 2
)
4x w ( w ) + 4x w −x + 4x w 6xw + 4x w ( −1) + 4x w 3x w
2 5 2 2 5
( 2
) 2 5 2 5
( 4 8
)
Multiply each term.
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
Verify answer has 5 terms like original parenthesis.

37. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w

38. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.

39. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.
Second term is degree 9.

40. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.
Second term is degree 9.
Third term is degree 10.

41. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.
Second term is degree 9.
Third term is degree 10.
Fourth term is degree 7.

42. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.
Second term is degree 9.
Third term is degree 10.
Fourth term is degree 7.
Fifth term is degree 19.

43. What is the degree of the previous
answer?
2 6 4 5 3 7 2 5 6 13
4x w − 4x w + 24x w − 4x w + 12x w
First term is degree 8.
Second term is degree 9.
Third term is degree 10.
Fourth term is degree 7.
Fifth term is degree 19.
Therefore, the polynomial is degree 19.

44. Try this one...
Multiply: ( 2
3x 2x − 5x + 7 )

45. Try this one...
Multiply: ( 2
3x 2x − 5x + 7 )
Distribute the monomial.

46. Try this one...
Multiply: ( 2
3x 2x − 5x + 7 )
Distribute the monomial.
( )
3x 2x + 3x ⋅ ( −5x ) + 3x ( 7 )
2

47. Try this one...
Multiply: ( 2
3x 2x − 5x + 7 )
( )
3x 2x + 3x ⋅ ( −5x ) + 3x ( 7 )
2
Multiply each term.

48. Try this one...
Multiply: ( 2
3x 2x − 5x + 7 )
( )
3x 2x + 3x ⋅ ( −5x ) + 3x ( 7 )
2
Multiply each term.
3 2
6x − 15x + 21x

49. What is the degree of the previous
answer?
3 2
6x − 15x + 21x

50. What is the degree of the previous
answer?
3 2
6x − 15x + 21x
First term is degree 3.

51. What is the degree of the previous
answer?
3 2
6x − 15x + 21x
First term is degree 3.
Second term is degree 2.

52. What is the degree of the previous
answer?
3 2
6x − 15x + 21x
First term is degree 3.
Second term is degree 2.
Third term is degree 1.

53. What is the degree of the previous
answer?
3 2
6x − 15x + 21x
First term is degree 3.
Second term is degree 2.
Third term is degree 1.
Therefore, the polynomial is degree 3.

54. Try this one...
Multiply: 2 2
( 3
−2a b a + 3a b − 4b2 3 5
)

55. Try this one...
Multiply: 2 2
( 3
−2a b a + 3a b − 4b 2 3 5
)
Distribute the monomial.

56. Try this one...
Multiply: 2 2
( 3
−2a b a + 3a b − 4b 2 3 5
)
Distribute the monomial.
( −2a b )( a ) + ( −2a b )( 3a b ) + ( −2a b )( −4b )
2 2 3 2 2 2 3 2 2 5

57. Try this one...
Multiply: 2 2
( 3
−2a b a + 3a b − 4b 2 3 5
)
( −2a b )( a ) + ( −2a b )( 3a b ) + ( −2a b )( −4b )
2 2 3 2 2 2 3 2 2 5
Multiply each term.

58. Try this one...
Multiply: 2 2
( 3
−2a b a + 3a b − 4b 2 3 5
)
( −2a b )( a ) + ( −2a b )( 3a b ) + ( −2a b )( −4b )
2 2 3 2 2 2 3 2 2 5
Multiply each term.
5 2 4 5 2 7
−2a b − 6a b + 8a b

59. What is the degree of the previous
answer?
5 2 4 5 2 7
−2a b − 6a b + 8a b

60. What is the degree of the previous
answer?
5 2 4 5 2 7
−2a b − 6a b + 8a b
First term is degree 7.

61. What is the degree of the previous
answer?
5 2 4 5 2 7
−2a b − 6a b + 8a b
First term is degree 7.
Second term is degree 9.

62. What is the degree of the previous
answer?
5 2 4 5 2 7
−2a b − 6a b + 8a b
First term is degree 7.
Second term is degree 9.
Third term is degree 9.

63. What is the degree of the previous
answer?
5 2 4 5 2 7
−2a b − 6a b + 8a b
First term is degree 7.
Second term is degree 9.
Third term is degree 9.
Therefore, the polynomial is degree 9.

64. Multiplying Polynomials
Watch this 6 minute video to learn how to multiply a
trinomial by a binomial.
Here’s the link to copy/paste if the hyperlink didn’t work: http://www.phschool.com/atschool/
academy123/english/academy123_content/wl-book-demo/ph-270s.html
The video shows you 2 methods, the horizontal method
and vertical method.
Alternative: Visit the PurpleMath website to learn how
to multiply polynomials using these methods.
The next slide will show you another method for
multiplying polynomials, called the box method.

65. Box method
The previous video showed you how to
multiply 2 polynomials, which can get messy.
The Box Method is a way to keep you
organized while multiplying.
Follow this link to see a 5 minute video
organizing the multiplication using boxes.
Here’s the link to copy/paste if the hyperlink doesn’t work: http://
www.slideshare.net/secret/iiYvYrvk1SxdrG

66. Practice Multiplying 2 Binomials
You’ve seen 3 different methods for multiplying polynomial: 1)
Horizontal Method; 2) Vertical Method; 3) Box Method
Practice your favorite method at Coolmath.
Select the “Give me a Problem” button to keep trying problems.
Do your work in a notebook.
When you select “What’s the Answer?” your answer is erased and
correct answer is displayed. Having your work in a notebook will
allow you to compare your answer to the correct answer.
Keep working problems until you get 4 out of 5 correct.
The next 2 slides show multiplying 2 binomials using the box method.

67. Example: ( 5x + 8 ) ( 3x − 1)

68. Example: ( 5x + 8 ) ( 3x − 1)
3x −1
5x
8

69. Example: ( 5x + 8 ) ( 3x − 1)
3x −1
5x 15x 2
5x
8 24x −8

70. Example: ( 5x + 8 ) ( 3x − 1)
2
3x −1 = 15x + 29x − 8
5x 15x 2
5x
8 24x −8

71. Example: ( 4n − 3) ( 3n − 2 )

72. Example: ( 4n − 3) ( 3n − 2 )
3n −2
4n
−3

73. Example: ( 4n − 3) ( 3n − 2 )
3n −2
4n 12n 2
−8n
−3 −9n 6

74. Example: ( 4n − 3) ( 3n − 2 )
2
3n −2 = 12n − 17n + 6
4n 12n 2
−8n
−3 −9n 6

75. Practice Multiplying 2 Polynomials
Now that you are an EXPERT at the easy problems, try some
harder problems at Coolmath. If you have trouble, go back and
review a method. Remember, you can also see me on Pronto!
Select the “Give me a Problem” button to keep trying problems.
Do your work in a notebook.
When you select “What’s the Answer?” your answer is erased and
correct answer is displayed. Having your work in a notebook will
allow you to compare your answer to the correct answer.
Keep working problems until you get 4 out of 5 correct.
The next 2 slides show multiplying 2 polynomials using the box
method.

76. Example: ( 4k + 3k + 9 ) ( k + 3)
2

77. Example: ( 4k + 3k + 9 ) ( k + 3)
2
2
4k 3k 9
k
3

78. Example: ( 4k + 3k + 9 ) ( k + 3)
2
2
4k 3k 9
k 3 2
4k 3k 9k
3 12k 2
9k 27

79. Example: ( 4k + 3k + 9 ) ( k + 3)
2
2
4k 3k 9
k 3 2
4k 3k 9k
3 12k 2
9k 27
3 2
= 4k + 15k + 18k + 27

80. Example: ( 2x − 3) ( 3x − 5x + 7 )
2

81. Example: ( 2x − 3) ( 3x − 5x + 7 )
2
2
3x −5x 7
2x
−3

82. Example: ( 2x − 3) ( 3x − 5x + 7 )
2
2
3x −5x 7
2x 3 2
6x −10x 14x
−3 −9x 2 15x −27

83. Example: ( 2x − 3) ( 3x − 5x + 7 ) 2
2
3x −5x 7
2x 3 2
6x −10x 14x
−3 −9x 2 15x −27
3 2
= 6x − 19x + 29x − 27

84. Extra Help
Here’s a cool site. Enter the polynomials
you wish to multiply and it gives you the
answer. A description of how to multiply
the polynomials is included.
If the above hyperlink doesn’t work, copy/
paste this link: http://www.webmath.com/
polymult.html

85. FANTASTIC job! You are
ready to Master the
Assignment. Good Luck!