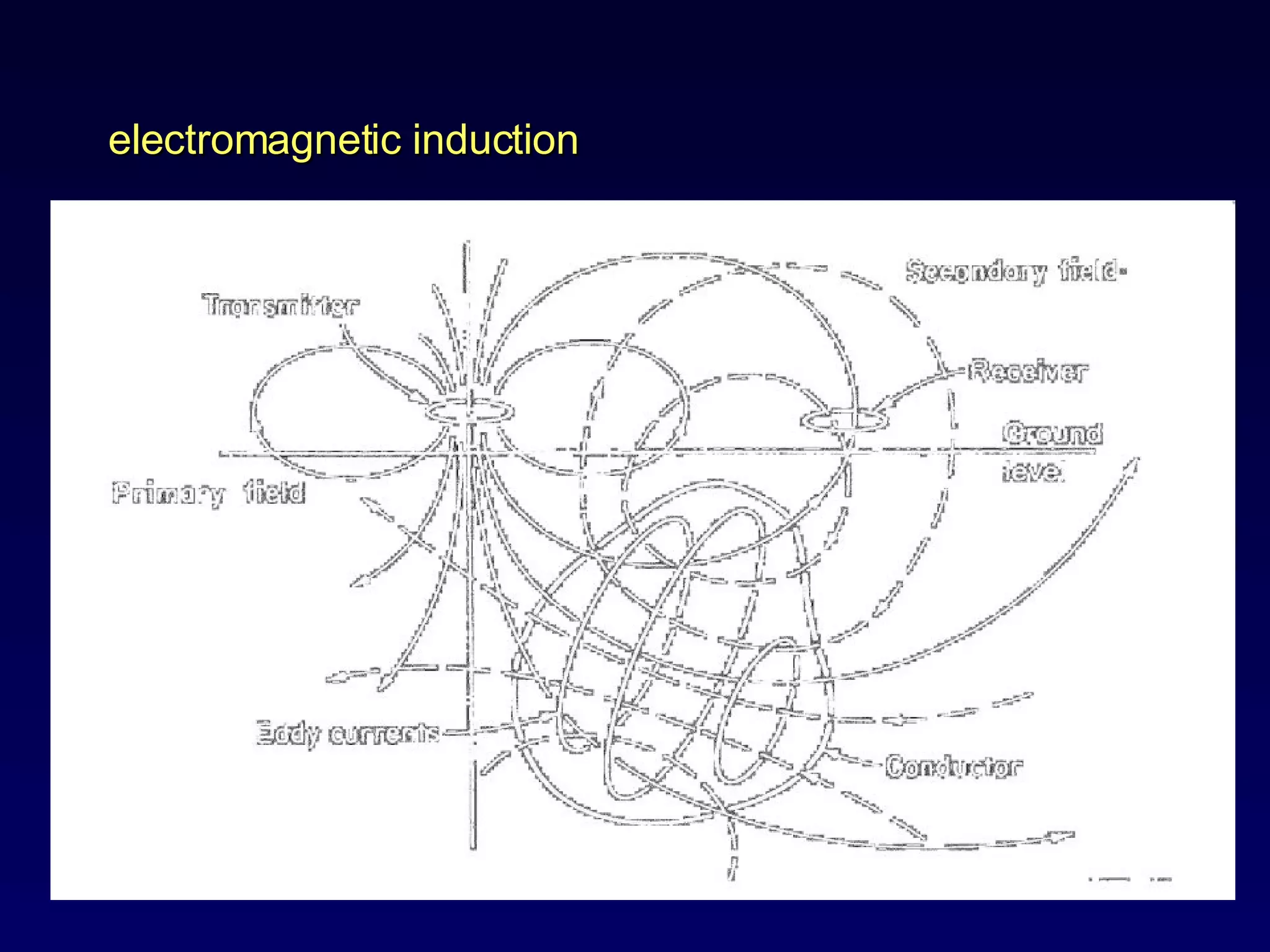
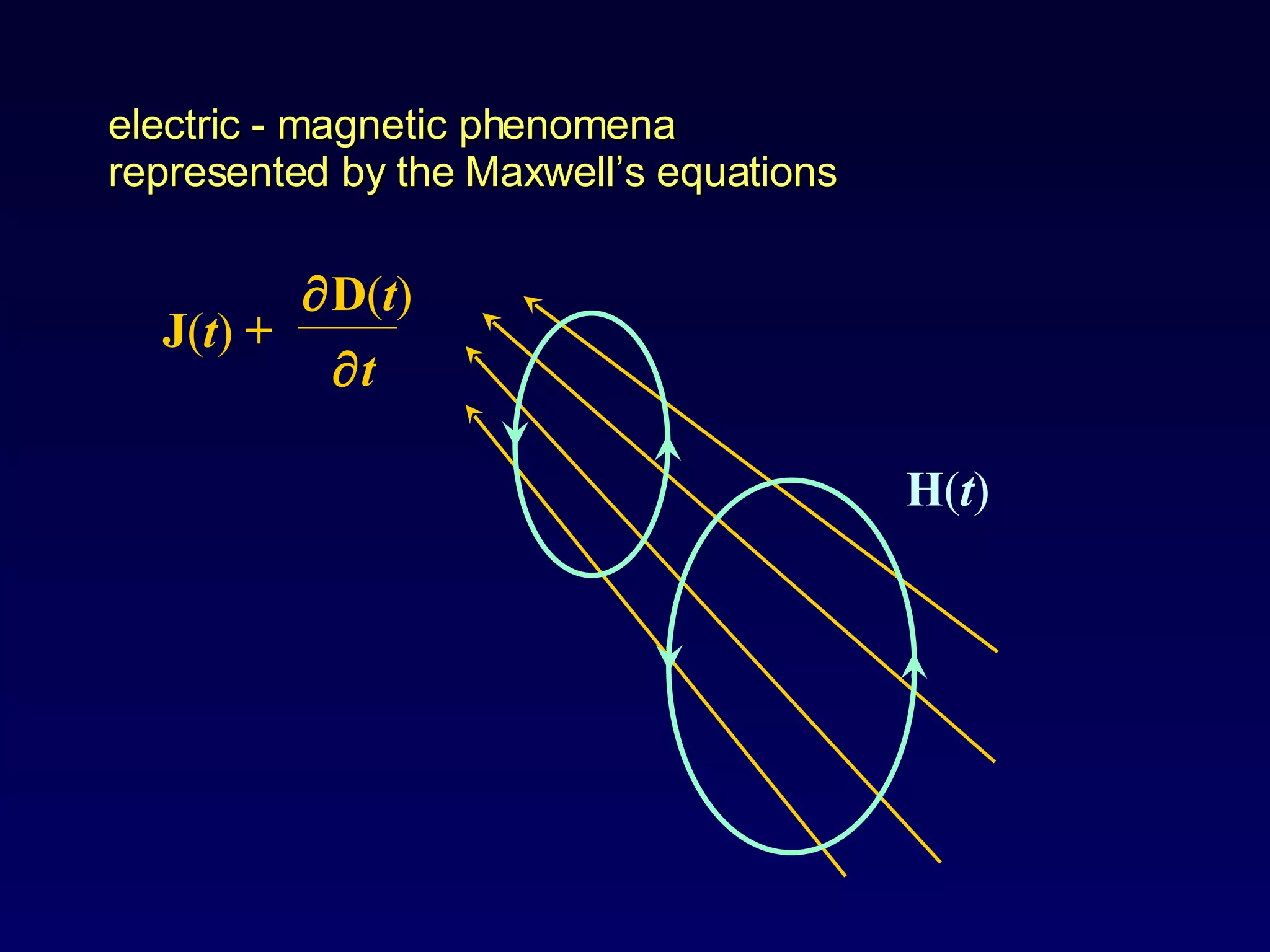
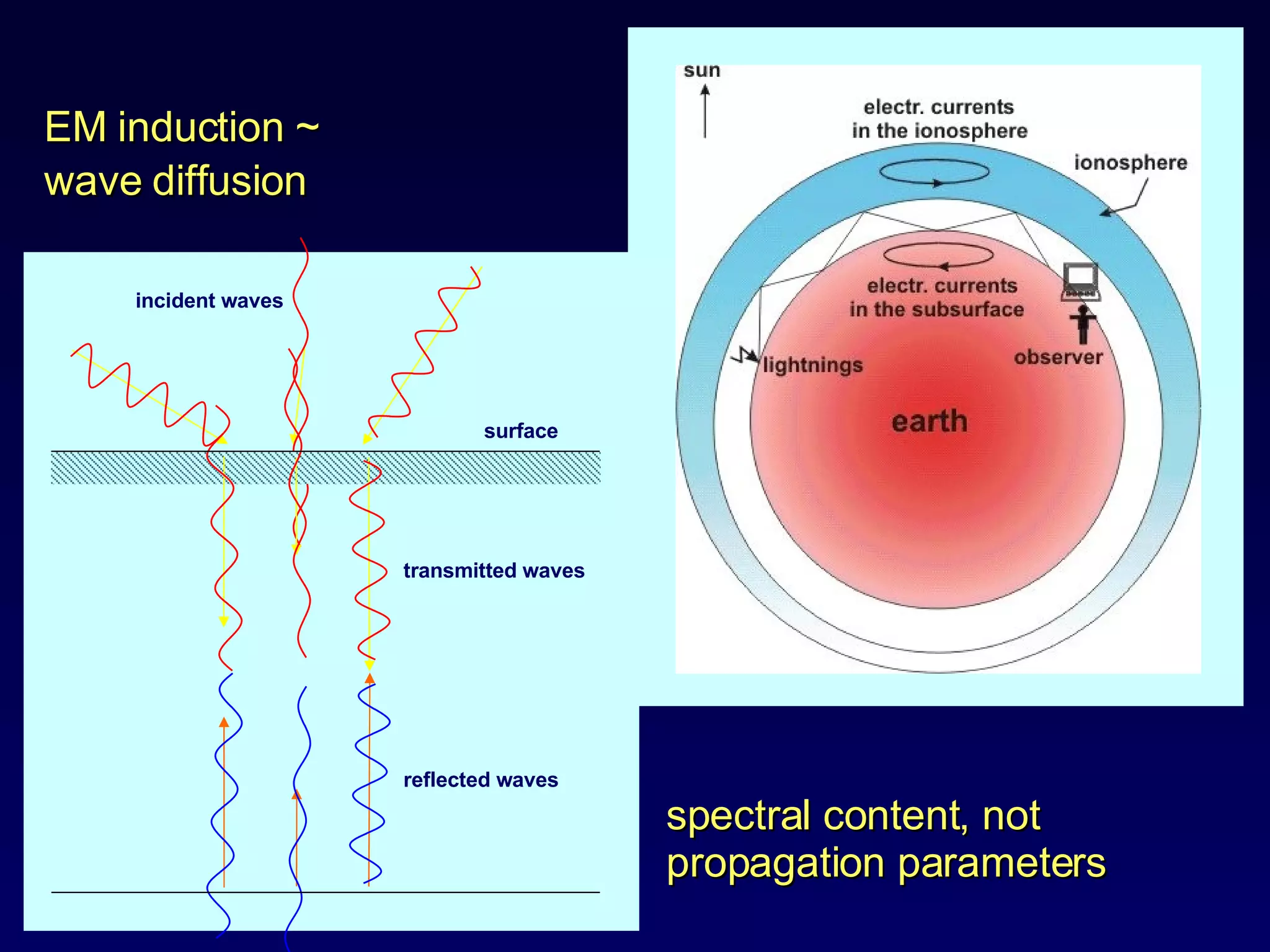
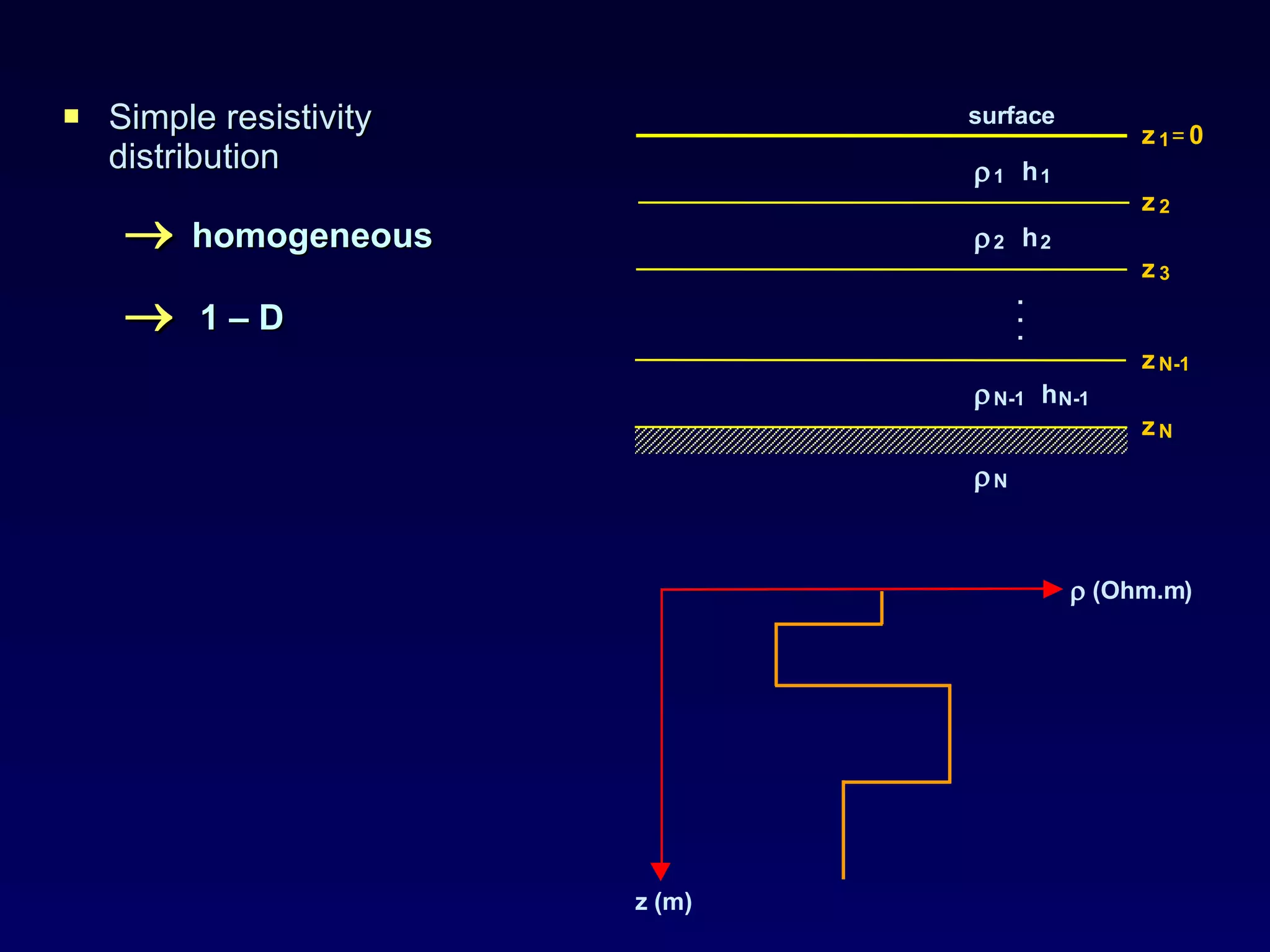
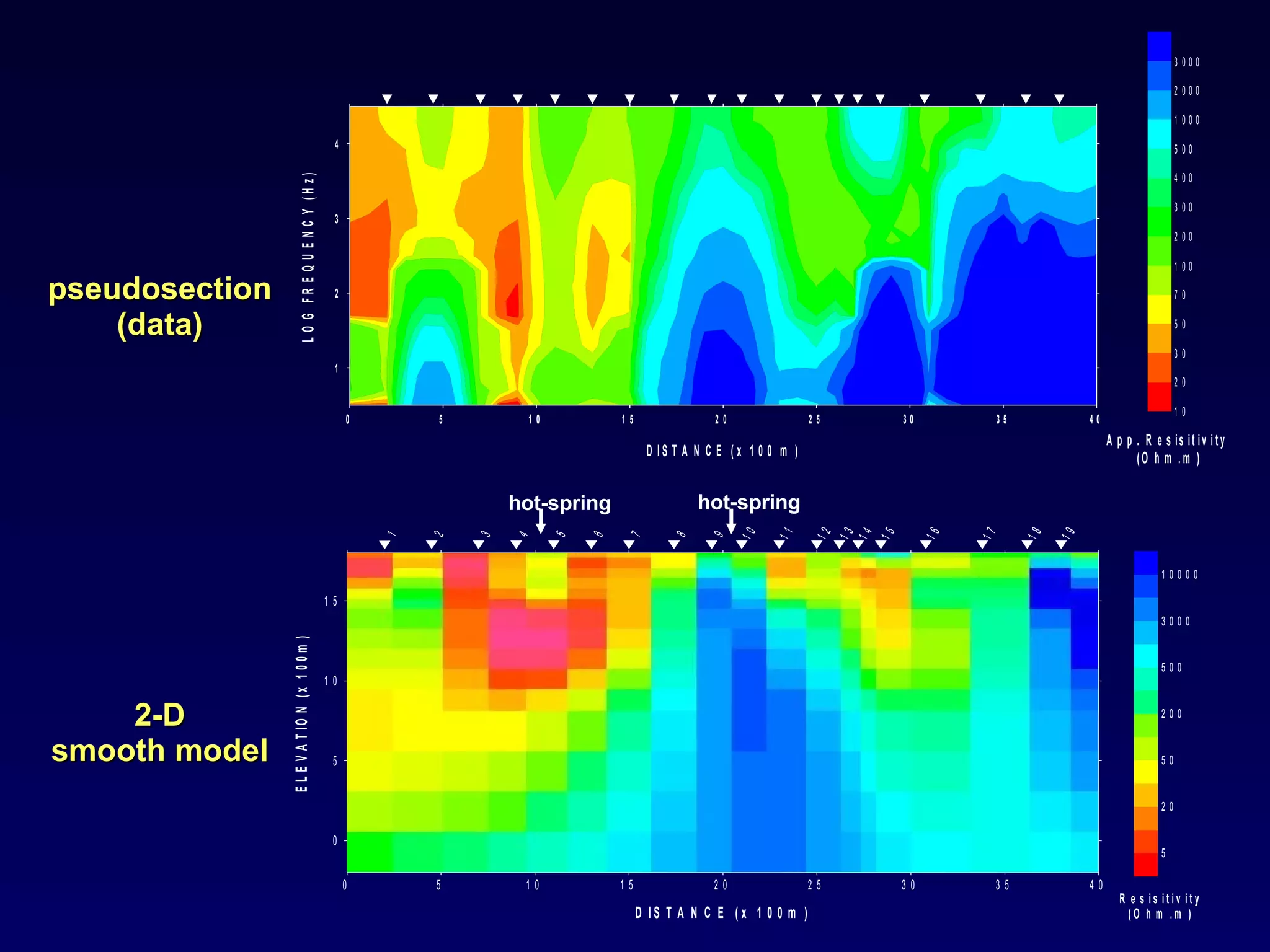
The document discusses the magnetotelluric (MT) method, which uses natural electromagnetic fields generated by solar winds and lightning to infer the conductivity and resistivity distribution of the subsurface. The MT method involves passive surface measurements of the earth's natural EM fields across a wide frequency range to investigate structures at intermediate to deep depths. Key aspects covered include skin effect, which causes exponential attenuation of EM waves with depth; MT data processing in the frequency domain; and 1D and 2D inversion modeling to estimate subsurface resistivity structures from measured impedance data.

1. MAGNETOTELLURIC (MT) METHOD

4. electromagnetic induction

5. natural electromagnetic field

6.  B ( t ) _______  t E ( t ) electric - magnetic phenomena represented by the Maxwell’s equations

7. H ( t ) electric - magnetic phenomena represented by the Maxwell’s equations  D ( t ) _______  t J ( t ) +

9. EM induction ~ wave diffusion spectral content, not propagation parameters incident waves transmitted waves surface reflected waves

15. Skin Effect and Penetration Depth

16. MT field set-up

17. MT field set-up

18. MT Time series data

19. Data processing sequence

20. E x = Z xx H x + Z xy H y E y = Z yx H x + Z yy H y  E = Z H  sounding curves Data Processing (Frequency Domain)  a = 0.2 T | Z | 2  = atan Im Z _______ Re Z

21. Modeling and Interpretation

25. 2-D resistivity section from 1-D models on a profile  correlation of resistivity units from station to station  correlation of resistivity units with geology and lithology

26. pseudosection (data) 2-D smooth model hot-spring hot-spring