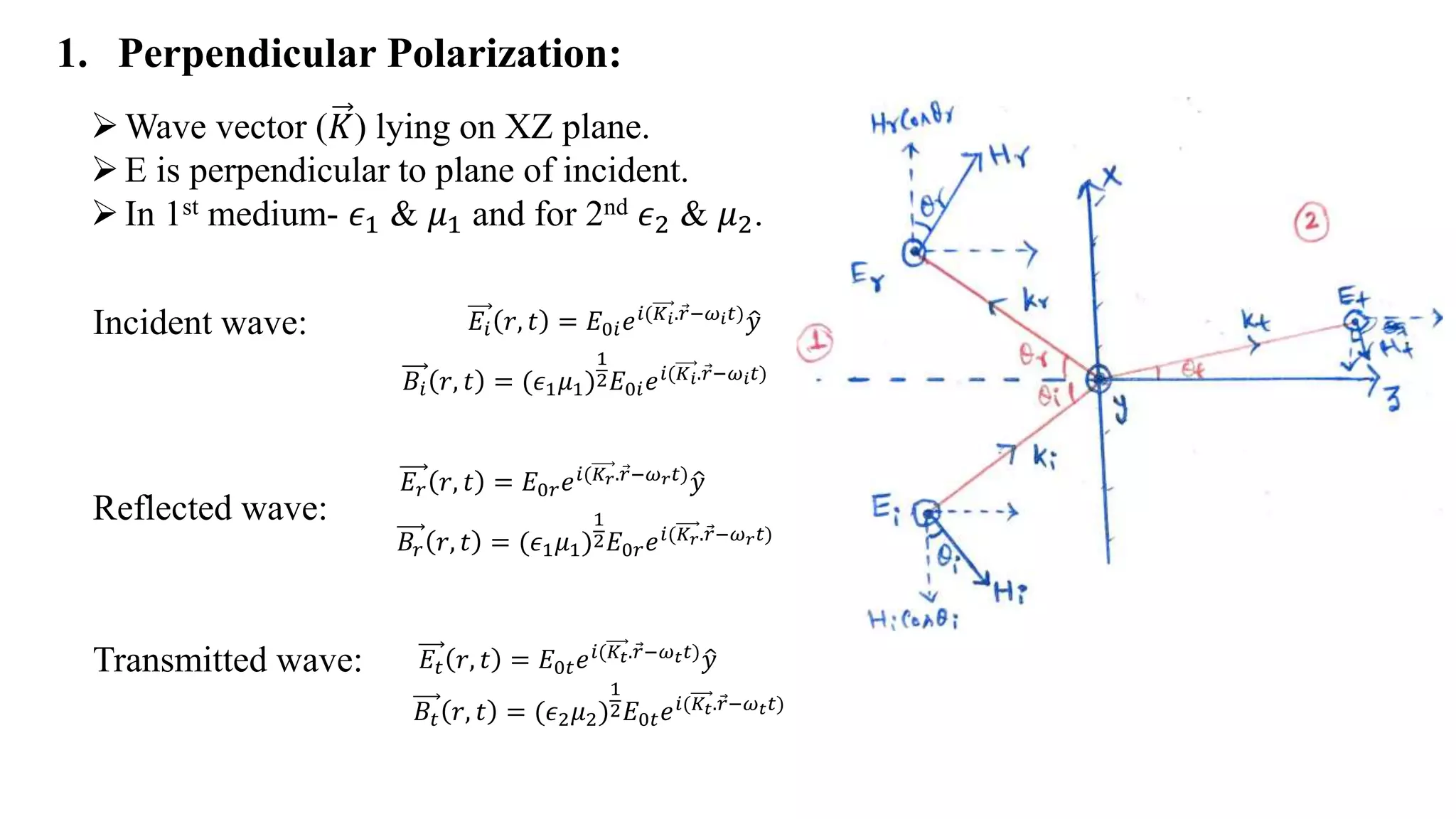
1. This document discusses the reflection and refraction of electromagnetic waves at boundaries between different media. It presents the boundary conditions and derives Fresnel's equations for both perpendicular and parallel polarizations.
2. Formulas are developed for the reflection and transmission coefficients relating to the electric field amplitudes. The coefficients satisfy the law of conservation of energy.
3. Special cases of normal incidence and reflection/refraction at a conducting medium are also considered. Complex refractive indices are introduced for conductors.