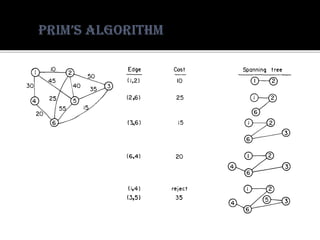
The document discusses greedy algorithms for solving optimization problems. It provides examples of using a greedy algorithm to solve the knapsack problem and the job sequencing problem. It also briefly mentions Prim's and Kruskal's algorithms for finding minimum spanning trees in graphs.

1. Kamalesh Karmakar,
Assistant Professor,
Dept. of C.S.E.
Meghnad Saha Institute of Technology

3. Algorithmsforoptimizationproblemstypicallygothroughasequenceofsteps,withasetofchoicesateachstep.Formanyoptimizationproblems,usingdynamicprogrammingtodeterminethebestchoicesisoverkill;simpler,moreefficientalgorithmswilldo.
Agreedyalgorithmalwaysmakesthechoicethatlooksbestatthemoment.Thatis,itmakesalocallyoptimalchoiceinthehopethatthischoicewillleadtoagloballyoptimalsolution.
Greedyalgorithmsdonotalwaysyieldoptimalsolutions,butformanyproblemstheydo.

5. Wearegivennobjectsandaknapsack.ObjectIhasanweightwiandtheknapsackhasthecapacitym.Ifafractionxi,0<=xi<=1ofobjectiisplacedintotheknapsack,thenaprofitofpixiisearned.
Objective:
maximizeΣpixi
1<=i<=n
maximizeΣwixi<=m
1<=i<=n
and0<=xi<=1,1<=I<=n
Afeasiblesolutionisanyset(x1,x2,…..,xn)satisfyingalltheabovesolution.

6. AlgorithmGeadyKnapsack(m,n)
/*p[1:n]andw[1:n]containtheprofitandweightsrespectivelyofthenobjectsorderedsuchthatp[i]/w[i]>=p[i+1]/w[i+1].Mistheknapsacksizeandx[1:n]isthesolutionvector.*/
{
fori:=1tondox[i]:=0.0;//Initialize
U:=m;
fori:=1tondo
{
if(w[i]>U)thenbreak;
x[i]:=1.0;U:=U–w[i];
}
if(i<=n)thenx[i]:=U/w[i];
}

7. High level description of Job Sequencing Algorithm

8. AlgorithmJS(d,j,n)
/*d[i]>=1,1<=i<=narethedeadlines,n>=1.Thejobsareorderedsuchthatp[1]>=p[2]>=….>=p[n].J[i]istheithjobintheoptimalsolution,1<=i<=k.Alsoatterminationd[J[i]]<=d[J[i+1]],1<=i<k*/
{
d[0]:=J[0]:=0;//Initialize.
J[1]:=1;//IncludeJob1.
k:=1;
fori:=2tondo
{
//Considerjobsinnon-increasingorderofp[i].Findposition
//ofIandcheckfeasibilityofinsertion.
r:=k;
while((d[J[r]]>d[i])and(d[J[r]]!=r))dor:=r-1;
if((d[J[r]<=d[i])and(d[i]>r))then
{
//InsertIintoJ[]
forq:=kto(r+1)step-1doJ[q+1]:=J[q];
J[r+1]:=i;k:=k+1;
}
}
returnk;
}

9. Prim’sAlgorithm
Kruskal’sAlgorithm