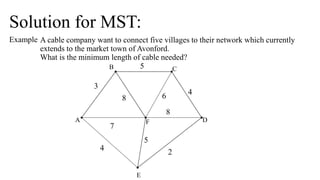
The document discusses greedy algorithms, which attempt to find optimal solutions to optimization problems by making locally optimal choices at each step that are also globally optimal. It provides examples of problems that greedy algorithms can solve optimally, such as minimum spanning trees and change making, as well as problems they can provide approximations for, like the knapsack problem. Specific greedy algorithms covered include Kruskal's and Prim's for minimum spanning trees.

1. Analysis and Design of Algorithms
(2150703)
Presented by :
Jay Patel (130110107036)
Gujarat Technological University
G.H Patel College of Engineering and Technology
Department of Computer Engineering
Greedy Algorithms
Guided by:
Namrta Dave

2. Greedy Algorithms:
• Many real-world problems are optimization problems in that they attempt to find an
optimal solution among many possible candidate solutions.
• An optimization problem is one in which you want to find, not just a solution, but the best
solution
• A “greedy algorithm” sometimes works well for optimization problems
• A greedy algorithm works in phases. At each phase: You take the best you can get right
now, without regard for future consequences.You hope that by choosing a local optimum at
each step, you will end up at a global optimum
• A familiar scenario is the change-making problem that we often encounter at a cash
register: receiving the fewest numbers of coins to make change after paying the bill for a
purchase.

3. • Constructs a solution to an optimization problem piece by
• piece through a sequence of choices that are:
1.feasible, i.e. satisfying the constraints
2.locally optimal (with respect to some neighborhood definition)
3.greedy (in terms of some measure), and irrevocable
• For some problems, it yields a globally optimal solution for every instance. For most, does
not but can be useful for fast approximations. We are mostly interested in the former case
in this class.
Greedy Technique:

4. Greedy Techniques:
• Optimal solutions:
• change making for “normal” coin denominations
• minimum spanning tree (MST)
• Prim’s MST
• Kruskal’s MST
• simple scheduling problems
• Dijkstra’s algo
• Huffman codes
• Approximations/heuristics:
• traveling salesman problem (TSP)
• knapsack problem
• other combinatorial optimization problems

5. Greedy Scenario:
• Feasible
• Has to satisfy the problem’s constraints
• Locally Optimal
• Has to make the best local choice among all feasible choices available on that step
• If this local choice results in a global optimum then the problem has optimal
substructure
• Irrevocable
• Once a choice is made it can’t be un-done on subsequent steps of the algorithm
• Simple examples:
• Playing chess by making best move without look-ahead
• Giving fewest number of coins as change
• Simple and appealing, but don’t always give the best solution

6. Change-Making Problem:
Given unlimited amounts of coins of denominations , give change for amount n with the least
number of coins
Example: d1 = 25 INR, d2 =10 INR, d3 = 5 INR, d4 = 1 INR and n = 48 INR
Greedy solution: <1, 2, 0, 3>
So one 25 INR coin
Two 10 INR coin
Zero 5 INR coin
Three 1 INR coin
But it doesn’t give optimal solution everytime.

7. Failure of Greedy algorithm
Example:
• In some (fictional) monetary system, “Coin” come in 1 INR, 7 INR, and 10 INR coins
Using a greedy algorithm to count out 15 INR, you would get
A 10 INR coin
Five 1 INR coin, for a total of 15 INR
This requires six coins
A better solution would be to use two 7 INR coin and one 1 INR coin
This only requires three coins
The greedy algorithm results in a solution, but not in an optimal solution

8. Knapsack Problem:
• Given n objects each have a weight wi and a value vi , and given a knapsack of total
capacity W. The problem is to pack the knapsack with these objects in order to maximize
the total value of those objects packed without exceeding the knapsack’s capacity.
• More formally, let xi denote the fraction of the object i to be included in the knapsack, 0 
xi  1, for 1  i  n. The problem is to find values for the xi such that
• Note that we may assume because otherwise, we would choose xi = 1 for each i
which would be an obvious optimal solution.
 

n
i
ii
n
i
ii vxWwx
11
maximized.isand
 

n
i
i Ww
1

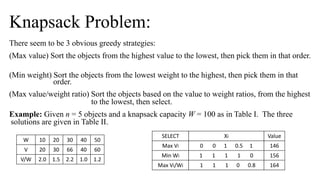
9. The optimal Knapsack Algorithm:
This algorithm is for time complexity O(n lgn))
(1) Sort the n objects from large to small based on the ratios vi/wi . We assume the
arrays w[1..n] and v[1..n] store the respective weights and values after sorting.
(2) initialize array x[1..n] to zeros.
(3) weight = 0; i = 1
(4) while (i  n and weight < W) do
(I) if weight + w[i]  W then x[i] = 1
(II) else x[i] = (W – weight) / w[i]
(III) weight = weight + x[i] * w[i]
(IV) i++

10. There seem to be 3 obvious greedy strategies:
(Max value) Sort the objects from the highest value to the lowest, then pick them in that order.
(Min weight) Sort the objects from the lowest weight to the highest, then pick them in that
order.
(Max value/weight ratio) Sort the objects based on the value to weight ratios, from the highest
to the lowest, then select.
Example: Given n = 5 objects and a knapsack capacity W = 100 as in Table I. The three
solutions are given in Table II.
Knapsack Problem:
W
V
V/W
10 20 30 40 50
20 30 66 40 60
2.0 1.5 2.2 1.0 1.2
Max Vi
Min Wi
Max Vi/Wi
SELECT Xi
0 0 1 0.5 1
1 1 1 1 0
1 1 1 0 0.8
Value
146
156
164

11. Minimum Spanning Tree (MST):
16 states of Spanning tree can happened

12. A cable company want to connect five villages to their network which currently
extends to the market town of Avonford.
What is the minimum length of cable needed?
A F
B C
D
E
2
7
4
5
8 6
4
5
3
8
Example
Solution for MST:

13. Kruskal’s Algorithm:
A F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
List the edges in order of size:
ED 2 AB 3
AE 4 CD 4
BC 5 EF 5
CF 6 AF 7
BF 8 CF 8
MST-KRUSKAL(G, w)
1. A ← Ø
2. for each vertex v V[G]
3. do MAKE-SET(v)
4. sort the edges of E into nondecreasing order
by weight w
5. for each edge (u, v) E, taken in
nondecreasing
order by weight
6. do if FIND-SET(u) ≠ FIND-SET(v)
7. then A ← A {(u, v)}
8. UNION(u, v)
9. return A

14. Select the shortest
edge in the network
ED 2
A F
B C
D
E
2
7
4
5
8 6 4
5
3
8
Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
A F
B C
D
E
2
7
4
5
8 6 4
5
3
8
1
43
2
Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4 (or AE 4)
A F
B
C
D
E
2
7
4 5
8 6 4
5
3
8
Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
A F
B C
D
E
2
7
4
5
8 6 4
5
3
8

15. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
BC 5 – forms a cycle
EF 5
A F
B
C
D
E
2
7
4
5
8 6 4
5
3
8
All vertices have been conn
The solution is
ED 2
AB 3
CD 4
AE 4
EF 5
A F
B C
D
E
2
7
4
5
8 6 4
5
3
8
5
6
Total weight of tree: 18
Kruskal’s Algorithm:

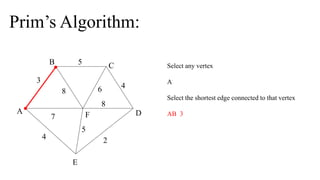
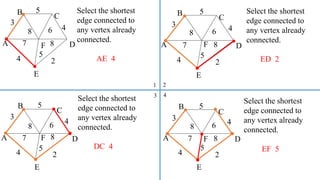
16. Prim’s Algorithm:
MST-PRIM(G, w, r)
1. for each u V [G]
2. do key[u] ← ∞
3. π[u] ← NIL
4. key[r] ← 0
5. Q ← V [G]
6. while Q ≠ Ø
7. do u ← EXTRACT-MIN(Q)
8. for each v Adj[u]
9. do if v Q and w(u, v) < key[v]
10. then π[v] ← u
11. key[v] ← w(u, v)

17. A F
B C
D
E
2
7
4
5
8 6 4
5
3
8
Select any vertex
A
Select the shortest edge connected to that vertex
AB 3
Prim’s Algorithm:

18. A F
B C
D
E
2
7
4
5
8 6 4
5
3
8
Select the shortest
edge connected to
any vertex already
connected.
AE 4
1
43
2
Select the shortest
edge connected to
any vertex already
connected.
ED 2
A F
B
C
D
E
2
7
4
5
8 6 4
5
3
8
Select the shortest
edge connected to
any vertex already
connected.
DC 4
A F
B
C
D
E
2
7
4
5
8 6 4
5
3
8
Select the shortest
edge connected to
any vertex already
connected.
EF 5
A F
B
C
D
E
2
7
4
5
8 6 4
5
3
8

19. Prim’s Algorithm:
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
All vertices have been connected.
The solution is
AB 3
AE 4
ED 2
DC 4
EF 5
Total weight of tree: 18

20. There are some methods left:
• Dijkstra’s algorithm
• Huffman’s Algorithm
• Task scheduling
• Travelling salesman Problem etc.
• Dynamic Greedy Problems
Greedy Algorithms:
We can find the optimized solution with Greedy method which may be optimal sometime.

21. THANK YOU