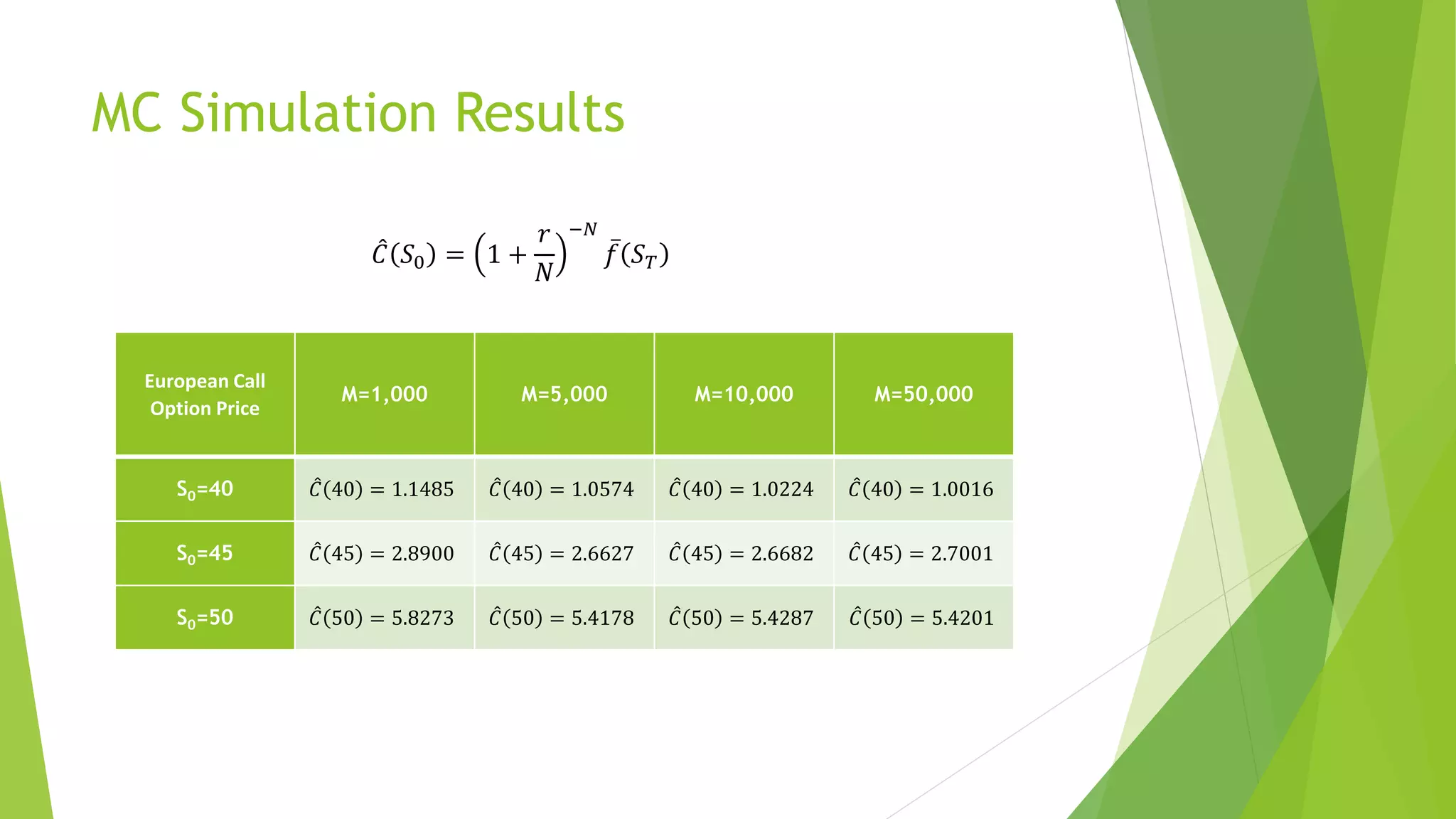
This document discusses using Monte Carlo simulation to price European call options. It begins by noting the uncertainty in underlying asset prices makes option pricing difficult. It then outlines the Monte Carlo simulation procedure of generating random price paths, calculating payoffs, and averaging. Key assumptions are presented for the stock price model and payoff calculation. Simulation results are shown for different numbers of simulations and compared to the Black-Scholes model, with error decreasing as the number of simulations increases.