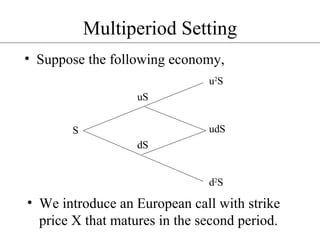
The document discusses binomial pricing models for pricing American options. It introduces a binomial model where the underlying asset price can move up or down between time periods. It shows how to price a European call option in this framework by constructing a replicating portfolio. The price of the option is set so that this portfolio replicates the payoffs. It then extends this to multiple time periods and discusses how to price early exercise features of American options.

1. Binomial Pricing Pricing of American Options

2. Introduction It is also based in an arbitrage argument. The option can be replicated with the underlying stock and bonds. Objective: Find the price of the option. Derive the replicating portfolio: basis of hedging and (therefore) investment banking.

3. Binomial Setting The price of the stock only can go up to a given value or down to a given value. Besides, there is a bond (bank account) that will pay interest of r. S uS dS

4. Binomial Setting (cont.) We assume u (up) > d (down). For Black and Scholes we will need d = 1/u For consistency we also need u > (1+r) > d. Example: u = 1.25; d = 0.80; r = 10%. S=100 S = 125 S = 80

5. Binomial Setting (cont.) Basic model that describes a simple world. As the number of steps increases, it becomes more realistic. We will price and hedge an option: it applies to any other derivative security. Key: we have the same number of states and securities (complete markets) Basis for arbitrage pricing.

6. Option Pricing Introduce an European call option: X = 110. It matures at the end of the period. S=100 uS = 125 dS = 80 S C (X=110) C u = 15 C d = 0

7. Option Pricing (cont.) We can replicate the option with the stock and the bond. Construct a portfolio that pays C u in state u and C d in state d. The price of that portfolio has to be the same as the price of the option. Otherwise there will be an arbitrage opportunity.

8. Option Pricing (cont.) We buy  shares and invest B in the bank. They can be positive (buy or deposit) or negative (shortsell or borrow). We want then, With solution,

9. Option Pricing (cont.) In our example, we get for stock: And, for bonds: The cost of the portfolio is,

10. Option Pricing (cont.) The price of the European call must be 9.09. Otherwise, there is an arbitrage opportunity. If the price is lower than 9.09 we would buy the call and shortsell the portfolio. If higher, the opposite. We have computed the price and the hedge simultaneously: We can construct a call by buying the stock and borrowing. Short call: the opposite.

11. Risk Neutral Pricing Remember that And Substituting,

12. Risk Neutral Pricing (cont.) After some algebra, Observe the coefficients, Positive. Smaller than one. Add up to one. Like a probability.

13. Risk Neutral Pricing (cont.) Rewrite Where This would be the pricing of: A risk neutral investor With subjective probabilities p and (1-p)

14. Multiperiod Setting Suppose the following economy, We introduce an European call with strike price X that matures in the second period. S uS dS u 2 S udS d 2 S

15. Multiperiod Setting (cont.) The price of the option will be: There are “two paths” that lead to the intermediate state (that explains the “2”).

16. Multiperiod Setting (cont.) Consider now n periods. Trick: count the minimum number of “up” movements that puts the call in the money. Call that number a, substitute above and get rid of 0.

17. Binomial Pricing The price of the European call becomes, Where, And  (a,n,p’) is the complementary binomial distribution. Probability of getting at least a “up” changes after n tosses with p’ the probability of “up” at each toss.

18. Binomial Pricing (cont.) The binomial distribution is tabulated.  (a,n,p’) is (approximately) the “delta” of the call: Number of shares (smaller than one) we need to replicate the European call. Suppose we know the volatility  and the time to maturity t. We can retrieve u and d:

19. American Options Objective: we want to value an American call that matures in two periods. Strike price, X = 100. Interest rate: 5% (each period). The underlying will pay a dividend of 8 after the first period. Problem: should we exercise after the first period or wait until maturity?

20. American Options (cont.) 100 Call Payoff 90 (82) 90.2 73.8 0 0 110 (102) 112.2 91.8 12.2 0 I II III In parenthesis: ex-dividend

21. American Options (cont.) Price of option at node II, 0: regardless of what happens afterwards the call pays zero. Price of call option at node I: If we exercise it (before the dividend is paid), 110-100 = 10. Unexercised: we compute the value of the replicating portfolio. Then, we compare.

22. American Options (cont.) Value of call:  Solution: exercise and get 10. Replicating portfolio: 110 (102) 112.2 91.8 12.2 0 I

23. American Options (cont.) At node III: Value of call: Replicating portfolio: 100 110 90 10 0 III