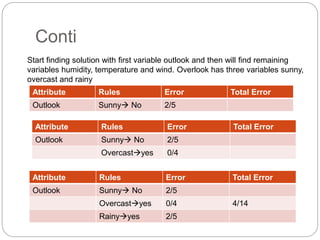
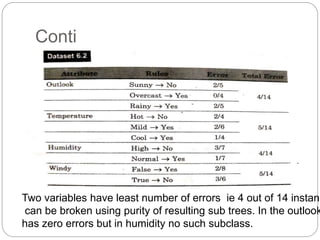
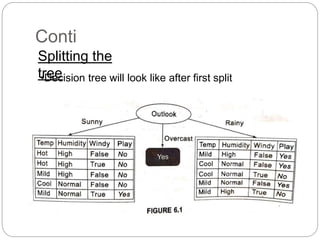
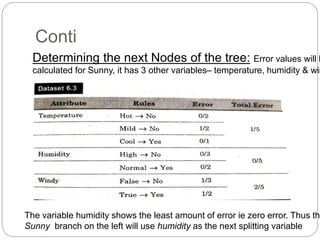
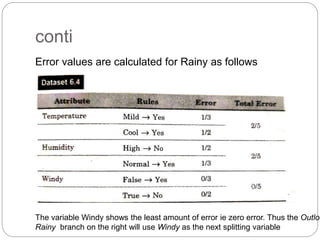
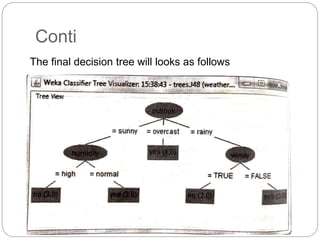
The document focuses on decision trees, emphasizing their structure, efficiency, and application in decision-making processes using past data points. It details steps for constructing a decision tree, including selecting variables, splitting criteria, and pruning methods to enhance predictive accuracy. The document also compares popular decision tree algorithms such as C4.5, CART, and CHAID, highlighting their characteristics and use cases.

1. Nandini V Patil
Asst.Professor
Godutai Engg. College Kalaburagi
Decision Trees

2. Introduction
 Decision tree are a simple way to guide one’s
path to a decision.
 Decision may be simple binary Eg. Approve of
loan or complex multi-valued decision Eg.
Sickness diagnosis
 Decision trees are hierarchically branched
structures that helps to come out to the decision
on asking certain questions.
 Good decision tree should short and ask only few
meaningful questions.
 Decision trees are very efficient to use, easy to
explain and their classification accuracy is
competitive with other methods.

3. Decision tree problem
 Experts will use decision tree or decision rules for
solving problems. Human experts Learns
experiences or data points. Similarly machine can be
trained to learn from the past data points and extract
some knowledge or rules from it.
 Predictive accuracy is based on the correct decision
made.
 The more data available for training the decision tree,
the more accurate its knowledge extraction, then it will
make more accurate decisions.
 The more variables the tree can choose from, the
greater is the accuracy of the decision tree.
 Good decision tree should frugal so that it takes the least
no of questions, thus least amount of effort to get to the

4. Conti
 Decision Problem: Create a decision tree that
helps to make decisions about approving for
playing out door games.
 The objective for predictions are atmospheric
conditions of that place.
 For answering this above question we need past
experiences what decisions are made in the
similar instances. The past data is as follows in
dataset 6.1
Outlook Temp Humidity Windy Play
Sunny Hot Normal True ??

5. Conti
We don’t have direct solution from the data set so we have to compute the

6. Decision tree construction
 Decision tree is a hierarchically branched structure.
 Creating a decision is based on asking few simple
questions more important question should be first and
then less important one.
Determining the root node of the tree
 Start the tree constructing by taking an example of
Weather problem for playing.
 Four choices for four variables –start with following
questions
 What is the outlook
 What is the temperature
 What is the humidity
 What is the wind speed

7. Conti
Attribute Rules Error Total Error
Outlook Sunny No 2/5
Attribute Rules Error Total Error
Outlook Sunny No 2/5
Overcastyes 0/4
Attribute Rules Error Total Error
Outlook Sunny No 2/5
Overcastyes 0/4 4/14
Rainyyes 2/5
Start finding solution with first variable outlook and then will find remaining
variables humidity, temperature and wind. Overlook has three variables sunny,
overcast and rainy

8. Conti
Two variables have least number of errors ie 4 out of 14 instanc
can be broken using purity of resulting sub trees. In the outlook
has zero errors but in humidity no such subclass.

9. Conti
Splitting the
tree•Decision tree will look like after first split

10. Conti
Determining the next Nodes of the tree: Error values will b
calculated for Sunny, it has 3 other variables– temperature, humidity & win
The variable humidity shows the least amount of error ie zero error. Thus the
Sunny branch on the left will use humidity as the next splitting variable

11. conti
Error values are calculated for Rainy as follows
The variable Windy shows the least amount of error ie zero error. Thus the Outloo
Rainy branch on the right will use Windy as the next splitting variable

12. Conti
The final decision tree will looks as follows

13. conti
Outlook Temp Humidity Windy Play
Sunny Hot Normal True ??
Outlook Temp Humidity Windy Play
Sunny Hot Normal True yes
Solve the current problem using the decision tree.
First question to ask is about outlook. Outlook is sunny, thus decision problem
moves to
sunny branch of the tree. In that, node has humidity subtree, in this problem
humidity is normal
thus branch leads to yes answer. Thus the answer to the play problem is yes.

14. Comparing Decision tree with table
lookup

15. Lessons from constructing trees
 Final decision tree has zero errors in mapping to the
prior data ie predictive accuracy of tree should be
100%.
 Algorithm should select the minimum no of variables
which are important to solve the problem.
 Tree is almost symmetric with all branches of almost
similar lengths.
 It may possible to increase predictive accuracy by
making more sub-trees & making the tree longer.
 Perfect fitting tree has the danger of over-fitting the
data, thus capturing all the random variations in the
data.
 There will be single best tree for this data, however
two or more equally efficient decision tree of similar
length with similar predictive accuracy for the same
dataset.

16. Decision tree Algorithms
 Decision tree is based on divide and conquer
method.
 Pseudo code for making decision tree is as
follows—
1. Create a root node & assign all of the training data
to it.
2. Select the best splitting attribute according to
certain criteria.
3. Add a branch to the root node for each value of
the split.
4. Split the data into mutually exclusive subsets
along the lines of the specific split.
5. Repeat steps 2 & 3 for each & every leaf node

17. Decision tree key elements
 Splitting criteria—
 Which variable to use for the first split? How should one determine the most
important variable for the first branch & subsequently for each subtree?
 Ans: Algorithms use different measures like least error, information gain,Gini’s coefficient.
 What values to use for the split? If the variables have continuous values such
as for age or blood pressure, what value-ranges should be used to make bins.
 How many branches should be allowed for each node? There could be binary
trees, with just two branches at each node. Or there could be more branches
allowed.
 Stopping criteria – When to stop building the tree? Two major ways–
a) When certain depth of the branches has been reached & tree becomes
unreachable after that.
b)When the error level at any node is within predefined tolerable levels.
 Pruning– Act of reducing the size of decision trees by removing sectins of
the tree that provide little value. The decision tree could be trimmed to make
it more balanced, more general &more easily usable. Two approaches in
pruning
 Prepruning
 Postpruning.

18. Comparing popular Decision tree
Algorithms
Decision
Tree
C4.5 CART CHAID
Fullname Iterative
Dichotomizer(ID3)
Classification and
Regression Trees
Chi-squar automatic
Interaction Detector
Basic
Algorithm
Huntis algorithm Huntis algorithm Adjusted significance
testing
Developer Ross Quinlan Bremman Gordon kass
When
developed
1986 1984 1980
Type of trees Classification Classification &
regression
Classification &
regression
Serial
implementati
on
Tree growth &
tree pruning
Tree growth & tree
pruning
Tree growth & tree
pruning
Type of data Discrete &
continuous;
Incomplete data
Discrete &
continuous;
Non-normal data also
accepted

19. Conti
Decision
Tree
C4.5 CART CHAID
Type of splits Multi-way Binary splits only;
clever surrogate
splits to reduce tree
depth
Multiway splits
as default
Splitting
criteria
Information gain Gini’s coefficient,&
other
Chi-square test
Pruning
criteria
Clever bottom-
up technique
avoid over-fitting
Remove weakest
links first
Trees can
become very
large
Implementati
on
Publically
available
Publically available
In most packages
Popular in
market research
for segmentation