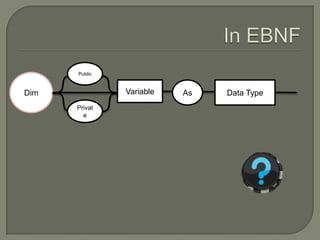
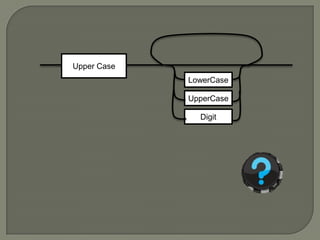
The document discusses metalanguages, specifically Backus-Naur Form (BNF) and Extended Backus-Naur Form (EBNF), highlighting their uses in representing syntax through text and diagrams. It explains the differences between BNF and EBNF, such as readability and handling of optional elements and repetition, and provides examples of EBNF syntax for legal statements in Visual Basic. The document serves as a guide for constructing EBNF diagrams for programming structures like 'if' statements.

1. Meta Languages BNF/EBNFKelly Bauer

2. 2 Basic Forms of metalanguageRailroad diagram (aka syntax structure diagrams)BNF/EBNF

3. Construct a railroad diagram of a legal if statement for Visual BasicHW

4. Railroad Diagrams

5. BNF/EBNFWere created to make it easier to represent syntax

6. Backus–Naur FormBNF is a text based metalanguage that is read right to left. This way, syntax can be represented by text, rather than diagrams

7. Extended Backus–Naur Form (EBNF)Invented to avoid the disadvantages of BNF. Easier to read, and less issues with things like repetition and optional elements

8. Is defined asBNFEBNF::=Boolean::=T|F=Boolean=T|F

9. Non-terminal ElementsBNFEBNF< ><Digit>::-0|1|2|<Letter>::-a|b|c< ><Digit>=0|1|2|<Letter>=a|b|c

10. Terminal Elements (eg, reserved words)BNFEBNFWritten as isDimIf01kWritten as isDimIf01k

11. SelectionBNFEBNFDefined as |Boolen::-T|FDefined as |Boolen=T|F

12. Optional ElementsBNFEBNFNo Optional Elements, so each option must be repeatedInteger::- - {<digit>} |{<digit>}[ ]Integer=[-] {<digit>}

13. RepetitionBNFEBNFNo repetitionRepetition through recursionRecursion is repetition achieved through a process calling itselfText page 170Indicated by { } Word={Letter}Repeated zero or more timesIf it needs to be repeated one or more times, it is written asWord=Letter{Letter}

14. an example

15. In EBNFPublicDimVariableAsData TypePrivate

16. SingleShortBooleanByteCharDateTimeDecimalDoubleIntLong

17. Upper CaseLowerCaseUpperCaseDigit

18. 0987654321

19. In Visual Basic Construct an EBNF diagram to describe a best practice, legal if statement. Should follow the following structure: If condition Then statements Else elsestatements

20. Syllabus Sections?