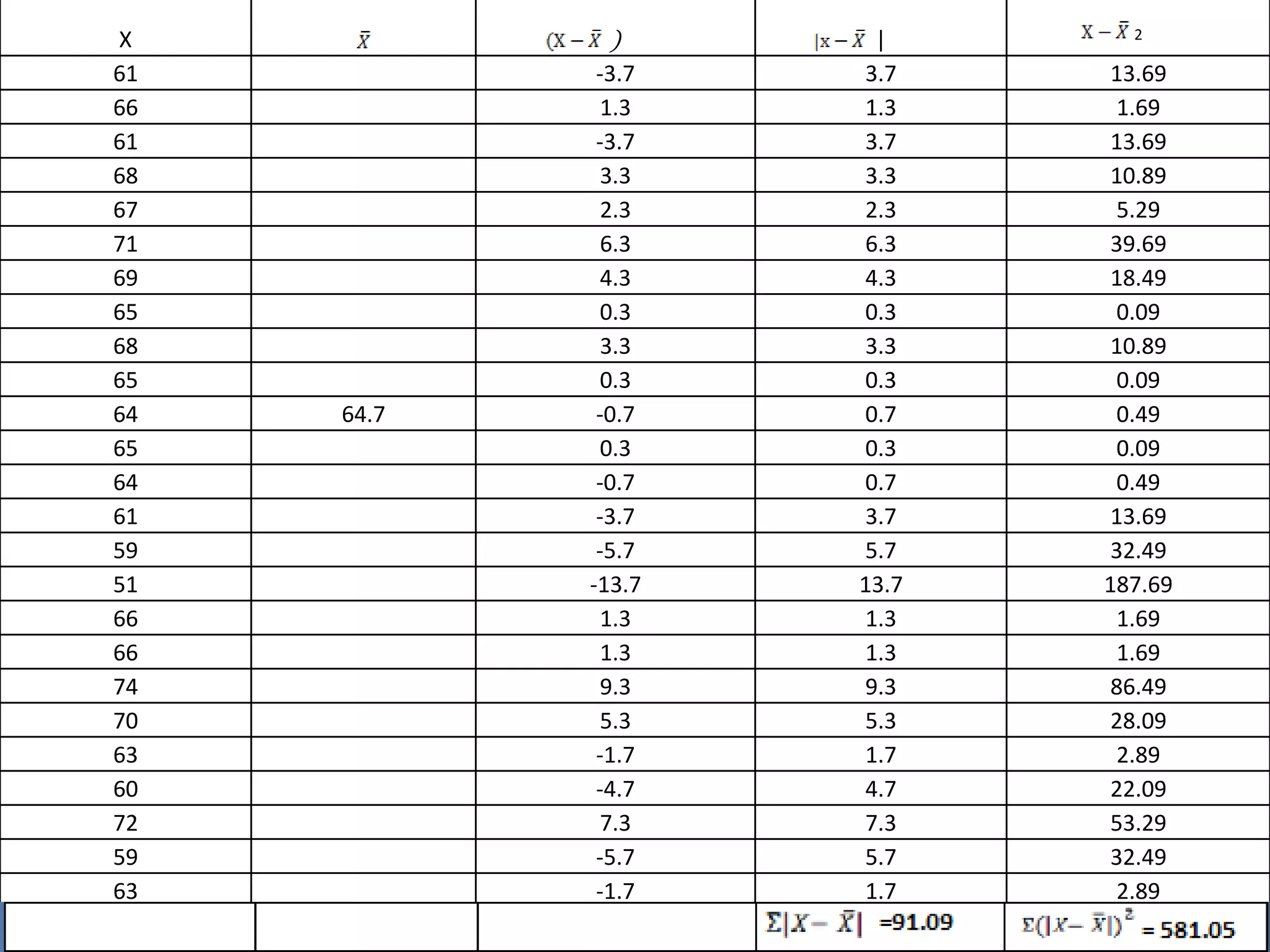
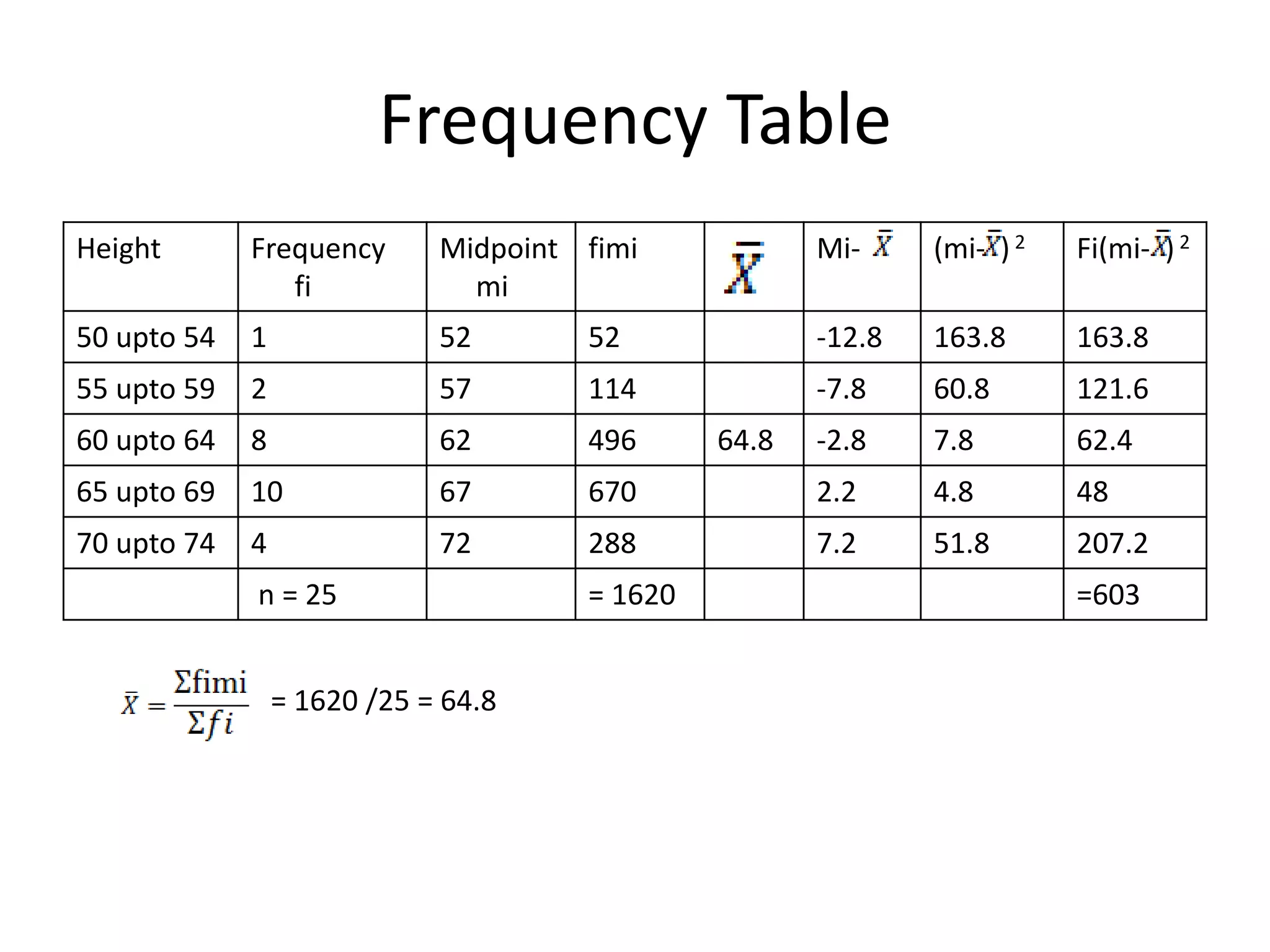
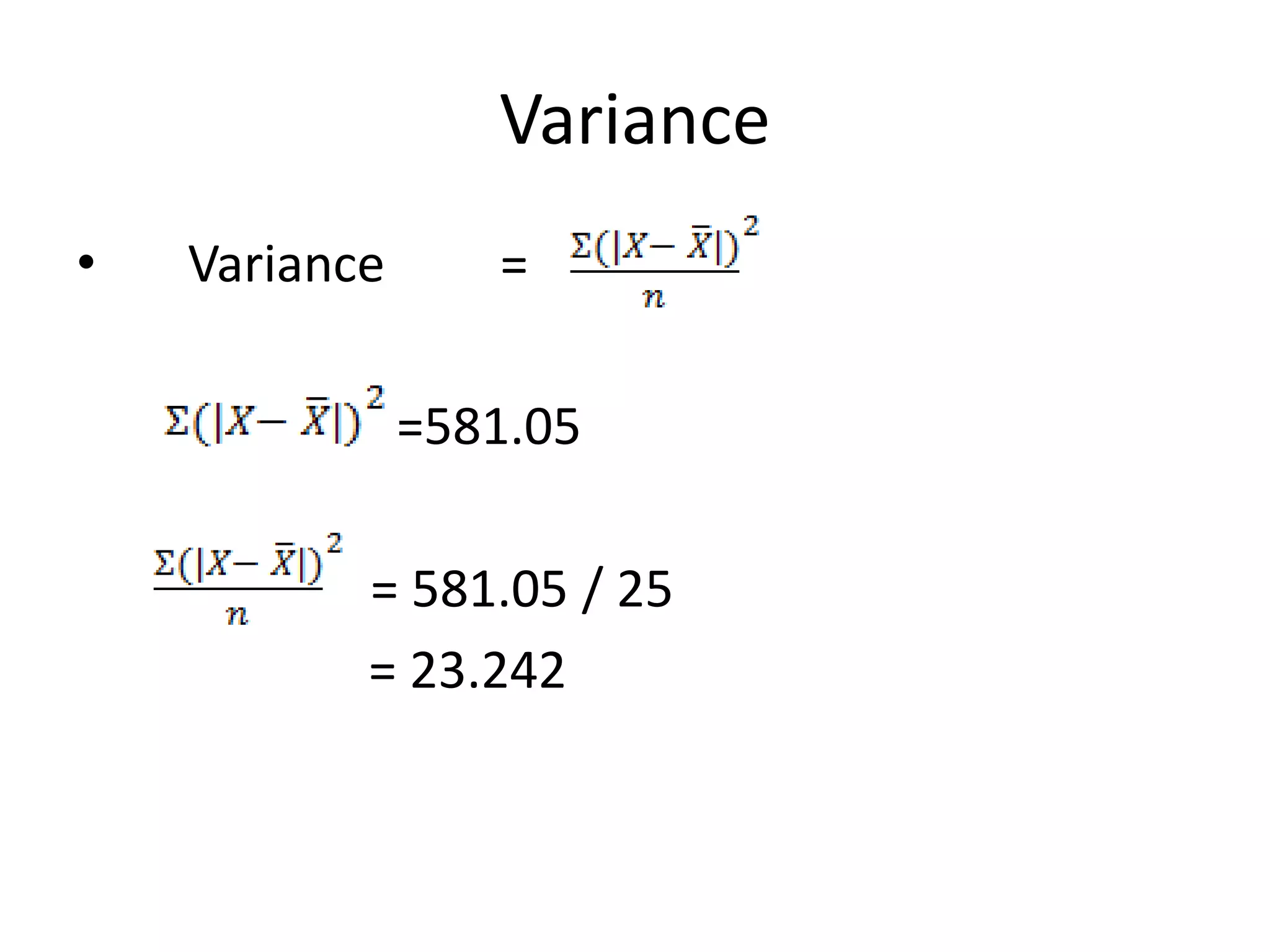This document presents information on measures of dispersion used to analyze student height data. It defines measure of dispersion as the average deviation from a central value to describe data spread. Formulas are provided for range, coefficient of range, mean deviation, variance, and standard deviation. Raw height data for 25 students is analyzed, finding a range of 23 inches, mean of 64.7 inches, and standard deviation of approximately 5 inches. Measures of dispersion are used to understand data homogeneity, mean reliability, and distribution comparisons.

1. Welcome To Our Presentation
Topic: Measure of Dispersion
Daffodil International University
Bangladesh.

2. What is Measure of Dispersion
• Measure of dispersion is defined as average
deviation of observations from some central
value.
To describe us about the spread of the data.
To compare the spread in two or more
distributions.
To calculate the lower limit and upper limit of
the observations under study.
Why Study Measure of dispersion?

3. Formula We are using.
• Range, n = x(n) - x(1)
• Here, x(n) = maximum value &
• x(1) = minimum value
• Coefficient of range = {(L-S)/(L+S)} X 100

4. Formula We are using.
• Mean deviation from mean =
• Variance =
• Standard Division S =

5. Raw Data
• We are collect 25 student’s height. (in inch)
61,66,61,68,67,71,69,65,68,65,64,65,64,61,59
,51,66,66,74,70,63,60,72,59,63
• Range = x(n) - x(1)
• = 74 - 51
• =23
coefficient of range :
= {(L-S)/(L+S)} X 100
= {(74-51)/(74+51)} X 100
= (23/125) X 100
= 18.4%

6. Mean
• =
1/25(61+66+61+68+67+71+69+65+68+65+64+
65+64+61+59+51+66+66+74+70+63+60+72+5
9+63)
• = 1/25*(1618)
• =64.7

7. X ) | 2
61 -3.7 3.7 13.69
66 1.3 1.3 1.69
61 -3.7 3.7 13.69
68 3.3 3.3 10.89
67 2.3 2.3 5.29
71 6.3 6.3 39.69
69 4.3 4.3 18.49
65 0.3 0.3 0.09
68 3.3 3.3 10.89
65 0.3 0.3 0.09
64 64.7 -0.7 0.7 0.49
65 0.3 0.3 0.09
64 -0.7 0.7 0.49
61 -3.7 3.7 13.69
59 -5.7 5.7 32.49
51 -13.7 13.7 187.69
66 1.3 1.3 1.69
66 1.3 1.3 1.69
74 9.3 9.3 86.49
70 5.3 5.3 28.09
63 -1.7 1.7 2.89
60 -4.7 4.7 22.09
72 7.3 7.3 53.29
59 -5.7 5.7 32.49
63 -1.7 1.7 2.89

8. Mean Deviation From Mean
= 91.09
=91.09/ 25
= 3.98

9. Variance
• Variance =
=581.05
= 581.05 / 25
= 23.242

10. Frequency Table
Height Frequency
fi
Midpoint
mi
fimi Mi- (mi- ) 2 Fi(mi- ) 2
50 upto 54 1 52 52 -12.8 163.8 163.8
55 upto 59 2 57 114 -7.8 60.8 121.6
60 upto 64 8 62 496 64.8 -2.8 7.8 62.4
65 upto 69 10 67 670 2.2 4.8 48
70 upto 74 4 72 288 7.2 51.8 207.2
n = 25 = 1620 =603
= 1620 /25 = 64.8

11. Standard Division From Grouped Data
• We Know That,
• S =
• =
• = 5.01
• =5

12. Advantages & Disadvantages
• Advantages:
• Easy to compute.
• Easy to understand.
• Scores exist in the data set.

13. Advantages & Disadvantages
• Disadvantages: -
• Value depends only on two scores. -Influenced
by sample size.
• Very sensitive to outliers. -Insensitive to the
distribution of scores within the two
extremes.
e.g. 1,2,2,3,4,6,7 vs. 1,1,1,1,1,1,7 both
have R=6

14. Application:
• Describe the homogeneity or heterogeneity of
the distribution.
• Understand the reliability of the mean.
• Compare the distributions as regards the
variability.
• Describe the relative standing of the data and
also shape of the distribution.

15. Review
• In summery we compute the range is 23 again
mean from raw data is about 64.7 and from
grouped data is about 64.8 . The coefficient of
range is about 18.4% . Standard division from
group data approximate 5.01 .