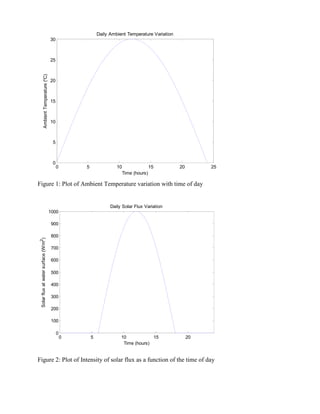
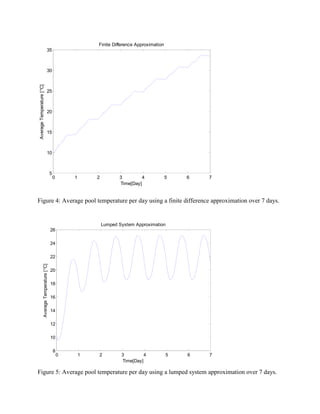
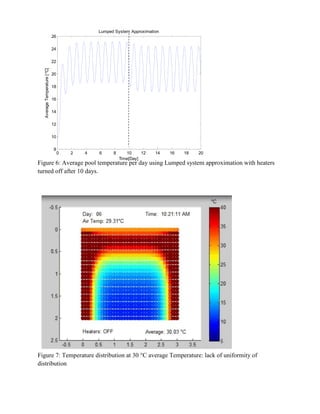
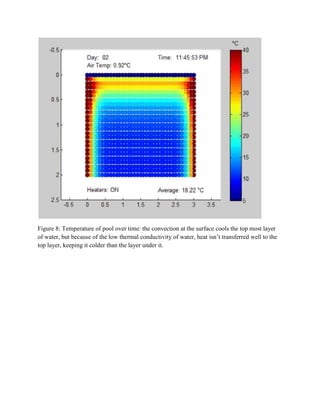
1) The document describes a study analyzing different methods to heat a swimming pool using solar radiation and electric heaters along the sides. 2) A finite difference method is used to model the pool as nodes and calculate heat transfer between nodes over time, predicting it would take 5 days and 11 hours to reach an average temperature of 30°C. 3) A lumped system approximation treats the pool as a single unit and predicts oscillating temperatures that never reach 30°C due to ambient heat losses exceeding heater output.

1. Pool Heating using Solar Radiation and Heating Elements<br />933450119380<br />Anthony Williams, Brandon Pak, Carlaton Wong,<br /> Jamil Khoury & Jonathan Wong<br />Group: DTM>JDM<br />ME 116A: Heat Transfer<br />Professor G. Aguilar<br />3 June 2010<br />Introduction: <br />In a world surrounded by the different facets of luxury, swimming pools are considered a novelty. They attract people during comfortable weather to come together and spend quality time with each other, and they serve as an attraction for playful children of all ages. In order to enjoy these outings, however, it is important that the swimming pool be of comfortable temperature, in order not to discourage swimmers sensitive to drastic temperature gradients relative to their own natural temperature. To solve this problem, we must use a preexisting design for heating a pool and model the heat transfer in order to verify that the pool temperature reaches an optimal 30º C. <br />Given Information: <br />The basic information was given as follows: the pool would be 2 meters deep, 3 meters wide, and ‘very’ long. The sides of the pools are covered by electric heaters, each of which provides a constant heat flux of 250 W/m2K, but only through the hours of 6 PM to 6 AM. The surface of the water would be exposed to the ambient air, which would be a source of convective heat transfer. The daily temperature distribution was given as sinusoidal ranging from 0 to 30º C from midnight to noon, respectively. Since wind speed was minimal, we were able to approximate the coefficient of convective heat transfer as 150 W/m2K. From 6 AM to 6 PM the pool was to encounter a solar radiation dependent on the time of day and depth of the water, which was incident in a sinusoidal manner. The solar flux was given as an equation dependent on the depth of the point in question and the time of day, or the intensity of sunlight. The penetration depth of sunlight was given as 0.3 meters.<br />With solar radiation and heaters along the sides of the pool as the main modes of heat transfer, we were to assume infinite pool length along the heated sides, and we were given the heat transfer rate relative to a unit of area. By modeling the pool as having one unit length, we were able to calculate the heat flux into the pool by the heaters alongside the pool, and the heat flux by solar radiation per unit length. We were to assume perfect insulation of the pool walls, standard water properties, and negligible evaporation.<br />We also assumed the fluid properties to be constant throughout the pool and do not change as a function of temperature. The following are tabulated fluid properties at T = 290 K, which is roughly the average temperature of the pool.<br />Thermal Conductivity: k=0.598 Wm∙K

2. Convection Coefficient: h=150 Wm2∙K

3. Specific Heat of Water: CP=4.184 kJkg∙K

4. Density of Water: ρ=1001 kgm3-174567-241069<br />Figure 1: Plot of Ambient Temperature variation with time of day<br />-91440159385<br />Figure 2: Plot of Intensity of solar flux as a function of the time of day<br />Calculations and Governing Equations:<br />From the schematic shown in Figure 1, there is a line of symmetry across the center of the pool, which will simplify the analysis by saving computation time. Based on the finite difference method, we calculated the heat influx and efflux at each ‘node’, which are arbitrarily placed points along the sides, by creating energy balances at each node. Since we know that q''conduction=-kdTdx, qconvection''=h(Ts-T∞), and qradiation''=I0(e-ziμ-e-z0μ), the energy balance of flux in and flux out yields the net flux in and out of each node, which equals the transient heat balance term qt''=mcpdTdt. Knowing that Ein-Eout+Egen=Estored, we balanced these equations for each node and generated the equations shown on the next page.<br />19050124617<br />qradiation\"
00<br />qconvection\"
<br />qheater\"
<br />Figure 3: Schematic of our Pool analysis: note the line of symmetry allowing for simplified calculations. Node Set 1 experiences the heat source, while Node Set 2 experiences solar flux. Node sets 3 and 4 are considered to be insulated.<br />Node C1 (Top Left Corner)

5. Node C2 (Top Right Corner)

6. Node C3 (Bottom Left Corner)

7. Node C4 (Bottom Right Corner)

8. Node Group 1 (Heater Wall Nodes)

9. Node Group 2 (Water Surface Nodes)