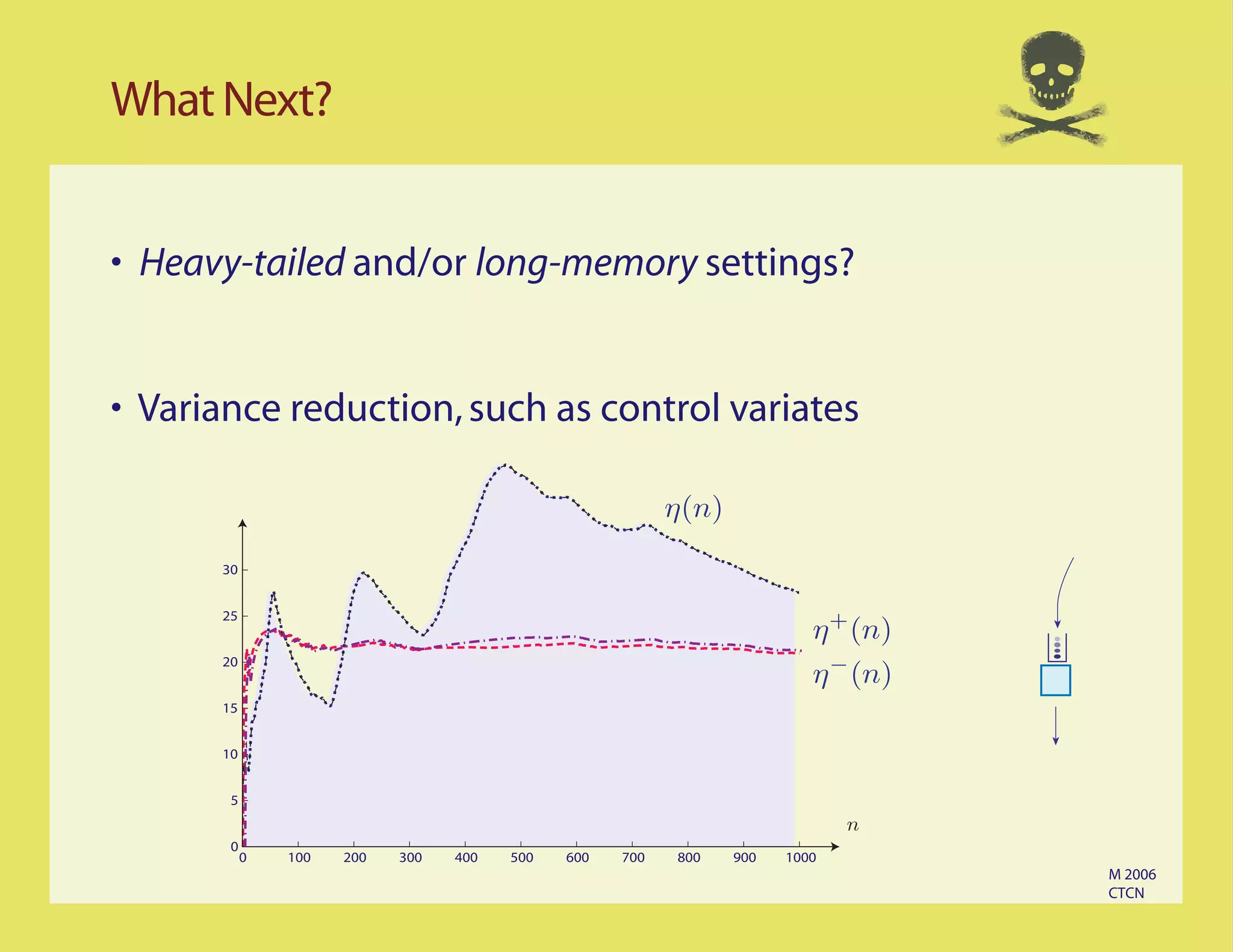
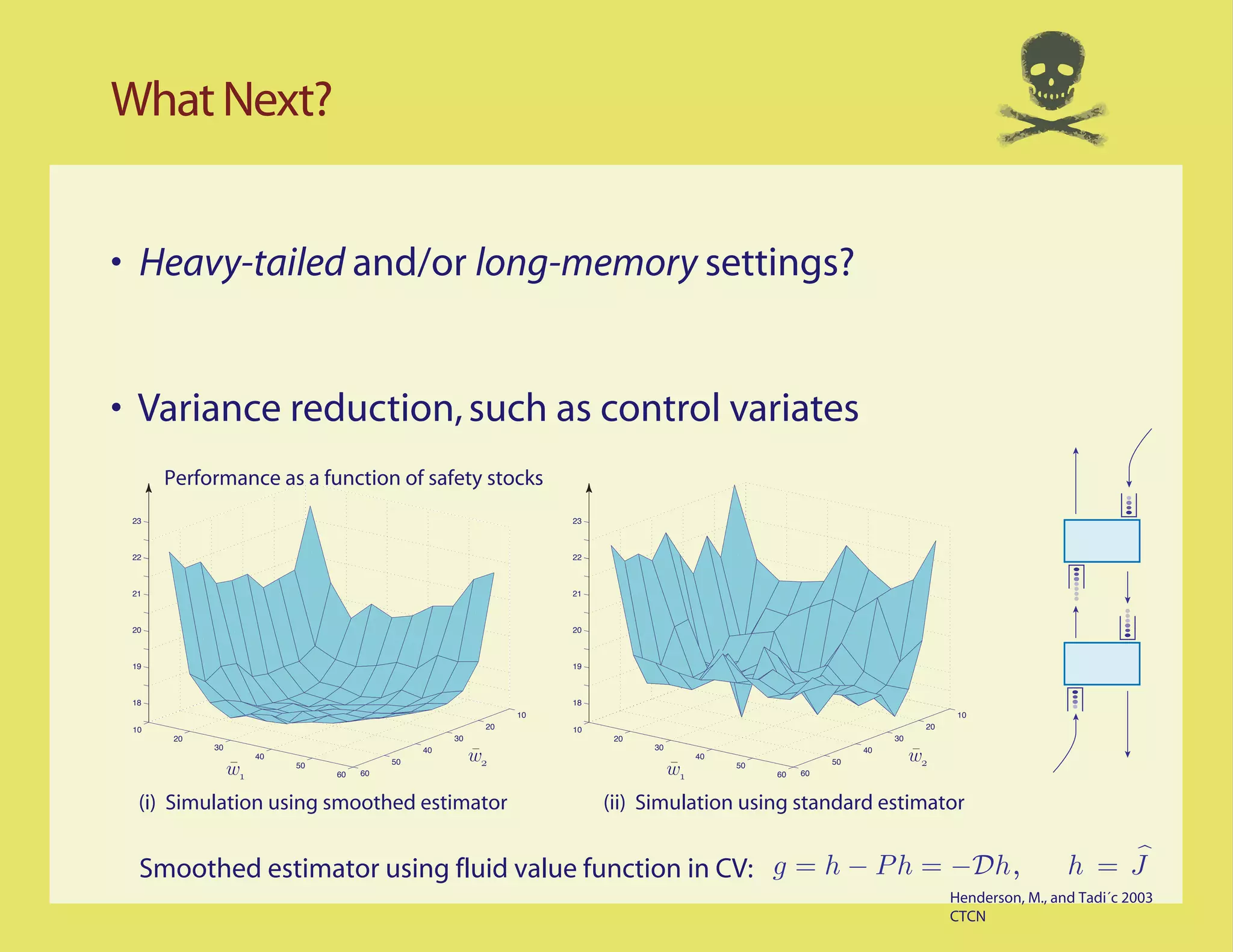
The document discusses the challenges of simulating reflected random walks (RRW) and the implications for queueing models, particularly the MM1 queue. It highlights the high variance in simulations during 'heavy traffic' and presents findings on sample-path behavior under large deviations. The document also suggests future research directions, including examining heavy-tailed or long-memory settings and variance reduction techniques.

1. Why are reflected random walks
so hard to simulate ?
Sean Meyn
Department of Electrical and Computer Engineering
and the Coordinated Science Laboratory
University of Illinois
Joint work with Ken Duffy - Hamilton Institute, National University of Ireland
NSF support: ECS-0523620

2. References
(Skip this advertisement)

3. Outline
Motivation
Reflected Random Walks
Why So Lopsided?
0 T
20
Theory:
Observed: X
Most Likely Paths
16
12
8
4
0
0 10 20 30 40 50
Summary and Conclusions

4. MM1 queue - the nicest of Markov chains
For the stable queue, with load strictly less than one, it is
• Reversible
• Skip-free
• Monotone
• Marginal distribution geometric
• Geometrically ergodic

5. MM1 queue - the nicest of Markov chains
For the stable queue, with load strictly less than one, it is
• Reversible
• Skip-free
• Monotone
• Marginal distribution geometric
• Geometrically ergodic
Why then, can’t I simulate my queue?

6. MM1 queue - the nicest of Markov chains
Ch 11 CTCN
1000
800
Gaussian density
600 Histogram
100,000
1
400
√ X(t) − η
100,000 t=1
200
MM1 queue
0 ρ = 0.9
−1000 −500 0 500 1000 1500 2000
Why then, can’t I simulate my queue?

7. II
Reflected Random Walk
t

8. Reflected Random Walk
A reflected random walk
where is the initial condition,
and the increments ∆ are i.i.d.

9. Reflected Random Walk
A reflected random walk
where is the initial condition,
and the increments ∆ are i.i.d.
Basic stability assumption:
and finite second moment

10. MM1 queue - the nicest of Markov chains
Reflected random walk with increments,
Load condition

11. Reflected Random Walk
A reflected random walk
where is the initial condition,
and the increments ∆ are i.i.d.
Basic stability assumption:
Basic question: Can I compute sample path averages
to estimate the steady-state mean?

12. Simulating the RRW: Asymptotic Variance
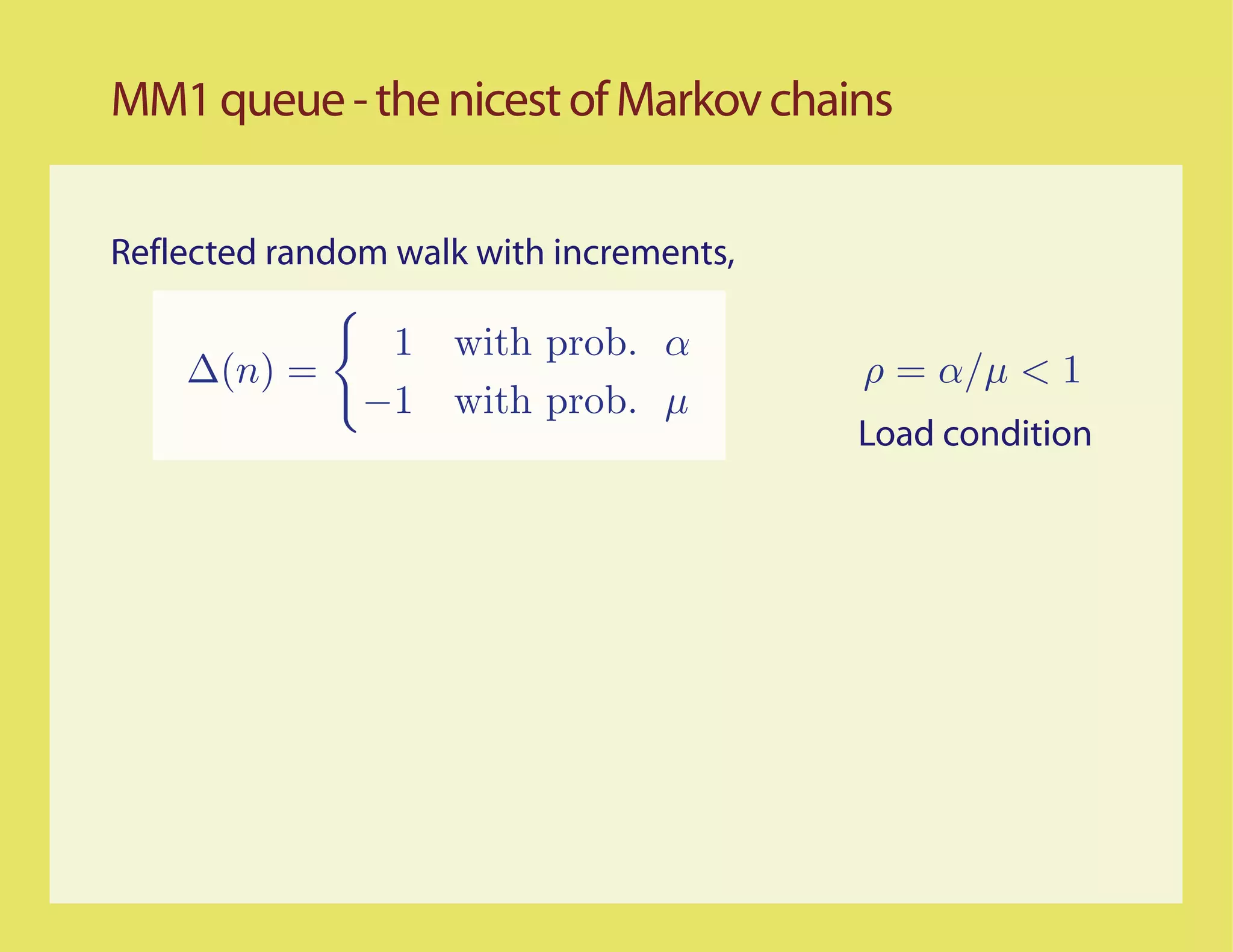
The CLT requires a third moment for the increments
E[∆(0)] < 0 and E[∆(0)3 ] < ∞
1
Asymptotic variance = O
(1 − ρ)4 Whitt 1989
Asmussen 1992

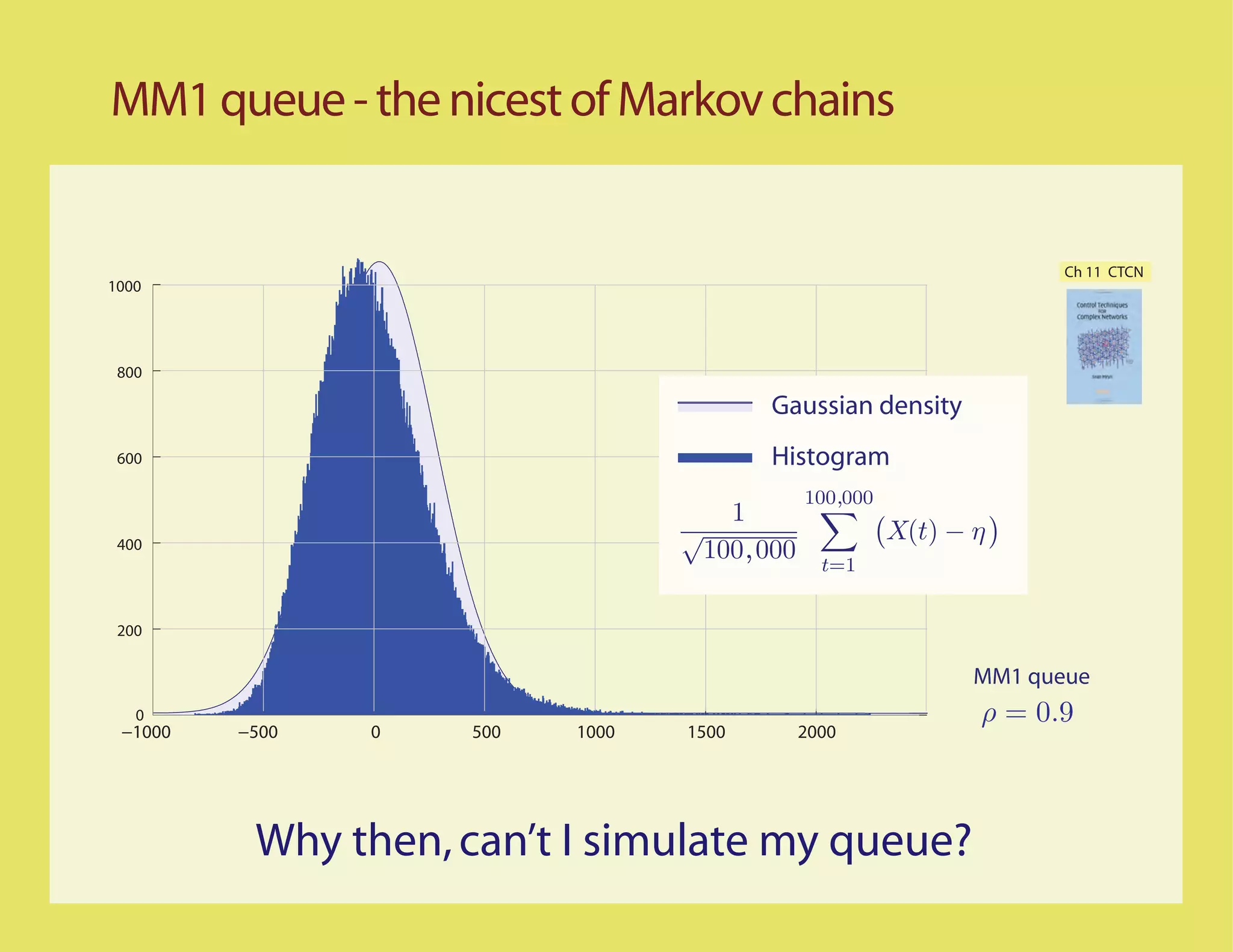
13. Simulating the RRW: Asymptotic Variance
The CLT requires a third moment for the increments
E[∆(0)] < 0 and E[∆(0)3 ] < ∞
1
Asymptotic variance = O
(1 − ρ)4
Ch 11 CTCN
1000
800
Gaussian density
600 Histogram
100,000
1
400
√ X(t) − η
100,000 t=1
200
MM1 queue
0 ρ = 0.9
−1000 −500 0 500 1000 1500 2000

14. Simulating the RRW: Lopsided Statistics
Assume only negative drift, and finite second moment:
E[∆(0)] < 0 and E[∆(0)2 ] < ∞
Lower LDP asymptotics: For each r < η ,
1
lim log P η(n) ≤ r
n→∞ n
= −I(r) < 0
M 2006

15. Simulating the RRW: Lopsided Statistics
Assume only negative drift, and finite second moment:
E[∆(0)] < 0 and E[∆(0)2 ] < ∞
Lower LDP asymptotics: For each r < η ,
1
lim log P η(n) ≤ r
n→∞ n
= −I(r) < 0
M 2006
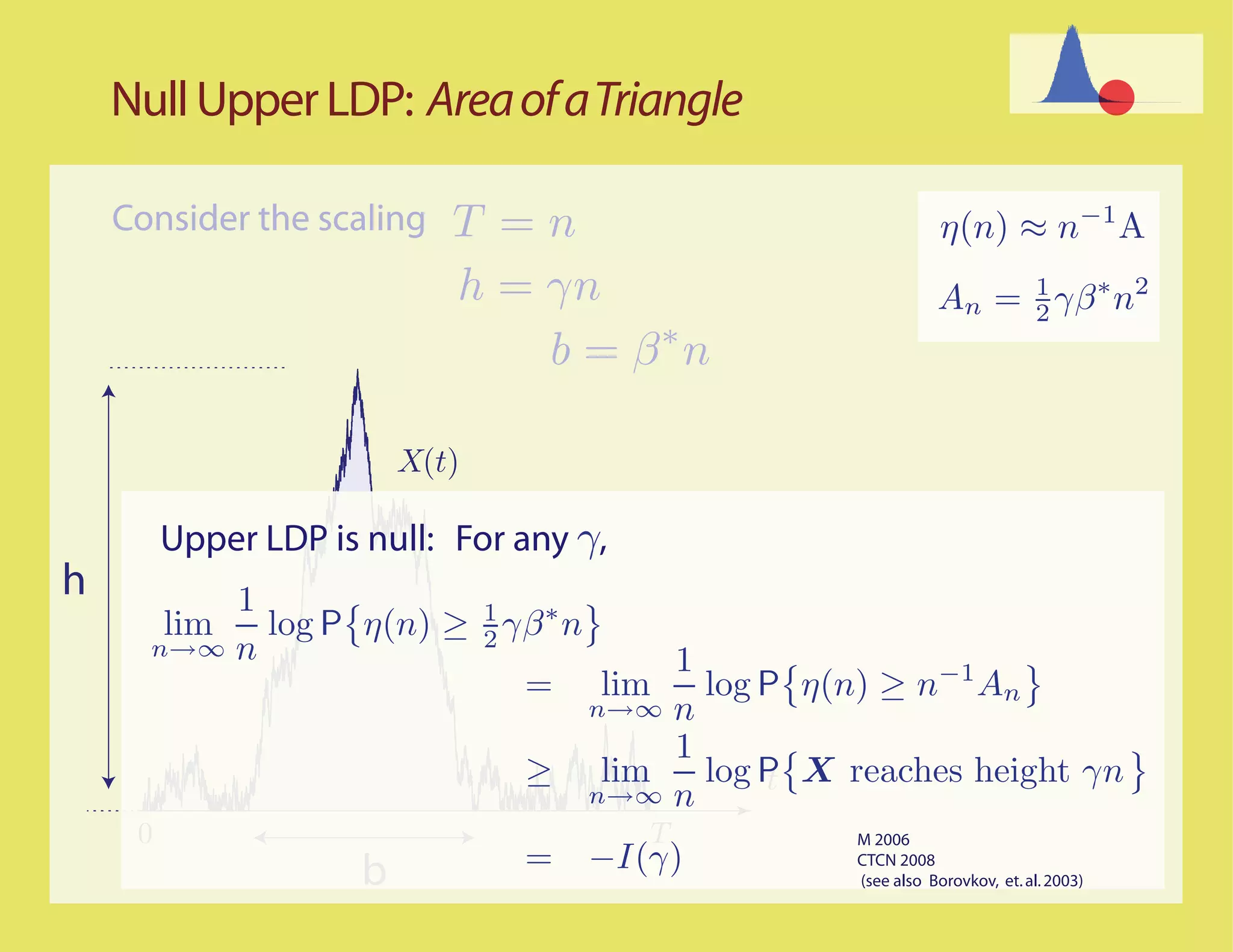
Upper LDP asymptotics are null: For each r ≥ η ,
1
lim log P η(n) ≥ r = 0 M 2006
n→∞ n CTCN
even for the MM1 queue!

16. III
Why So Lopsided?

17. Lower LDP
Construct the family of twisted transition laws
ˇ ˇ
ˇ (x, dy) = eθx−Λ(θ)+F (x) P (x, dy)eF (y)
P θ<0

18. Lower LDP
Construct the family of twisted transition laws
ˇ ˇ
ˇ (x, dy) = eθx−Λ(θ)+F (x) P (x, dy)eF (y)
P θ<0
Geometric ergodicity of the twisted chain implies multiplicative
ergodic theorems, and thence Bahadur-Rao LDP asymptotics
Kontoyiannis & M 2003, 2005
M 2006

19. Lower LDP
Construct the family of twisted transition laws
ˇ ˇ
ˇ (x, dy) = eθx−Λ(θ)+F (x) P (x, dy)eF (y)
P θ<0
Geometric ergodicity of the twisted chain implies multiplicative
ergodic theorems, and thence Bahadur-Rao LDP asymptotics
Kontoyiannis & M 2003, 2005
M 2006
This is only possible when θ is negative

20. Null Upper LDP: What is the area of a triangle?
1
A= 2 bh
h
b

21. Null Upper LDP: What is the area of a triangle?
1
A= 2 bh
X(t)
η(n) ≈ n−1 A
h
t
0 T
b

22. Null Upper LDP: Area of a Triangle?
Consider the scaling T =n η(n) ≈ n−1 A
h = γn Base obtained from most
likely path to this height:
b = β∗n
e.g., Ganesh, O’Connell, and Wischik, 2004
X(t)
Large deviations for reflected random walk:
h
t
0 T
b

23. Null Upper LDP: Area of a Triangle
Consider the scaling T =n η(n) ≈ n−1 A
h = γn An = 1 γβ ∗ n2
2
b = β∗n
X(t)
Upper LDP is null: For any γ,
h
t
0 T M 2006
b CTCN 2008
(see also Borovkov, et. al. 2003)

24. IV
Most Likely Paths

25. What Is The Most Likely Area?
Are triangular excursions optimal?
Most likely path?
t
0 T

26. What Is The Most Likely Area?
Triangular excursions are not optimal:
Better...
t
0 T
A concave perturbation: greatly increased
area at modest “cost”

27. Better...
Most Likely Paths t
0 T
Scaled process
ψ n (t) = n−1 X(nt)
LDP question translated to the scaled process
Duffy and M 2009, ...

28. Better...
Most Likely Paths t
0 T
Scaled process
ψ n (t) = n−1 X(nt)
LDP question translated to the scaled process
1
η(n) ≈ An ⇐⇒ ψ n (t) dt ≈ A
0

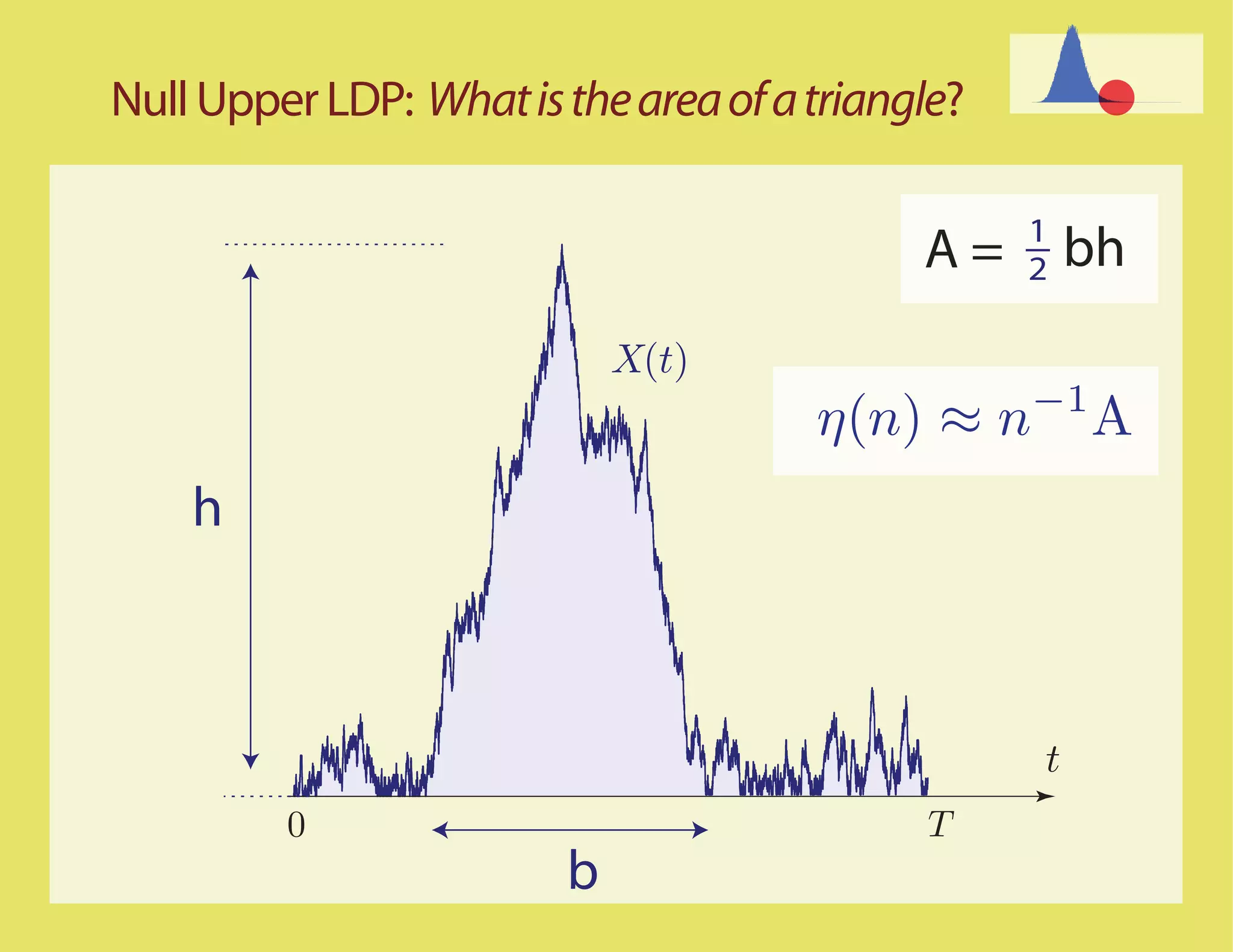
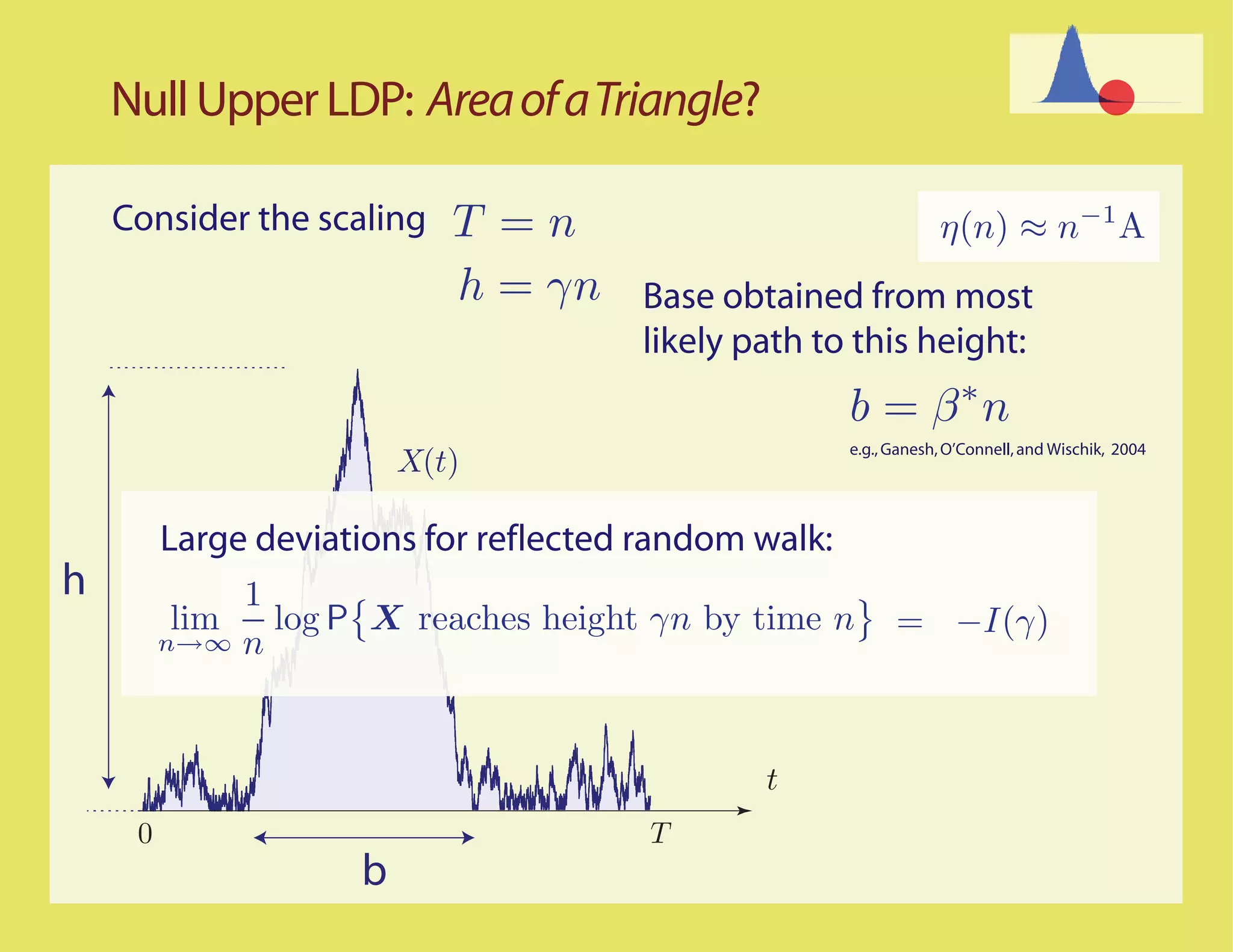
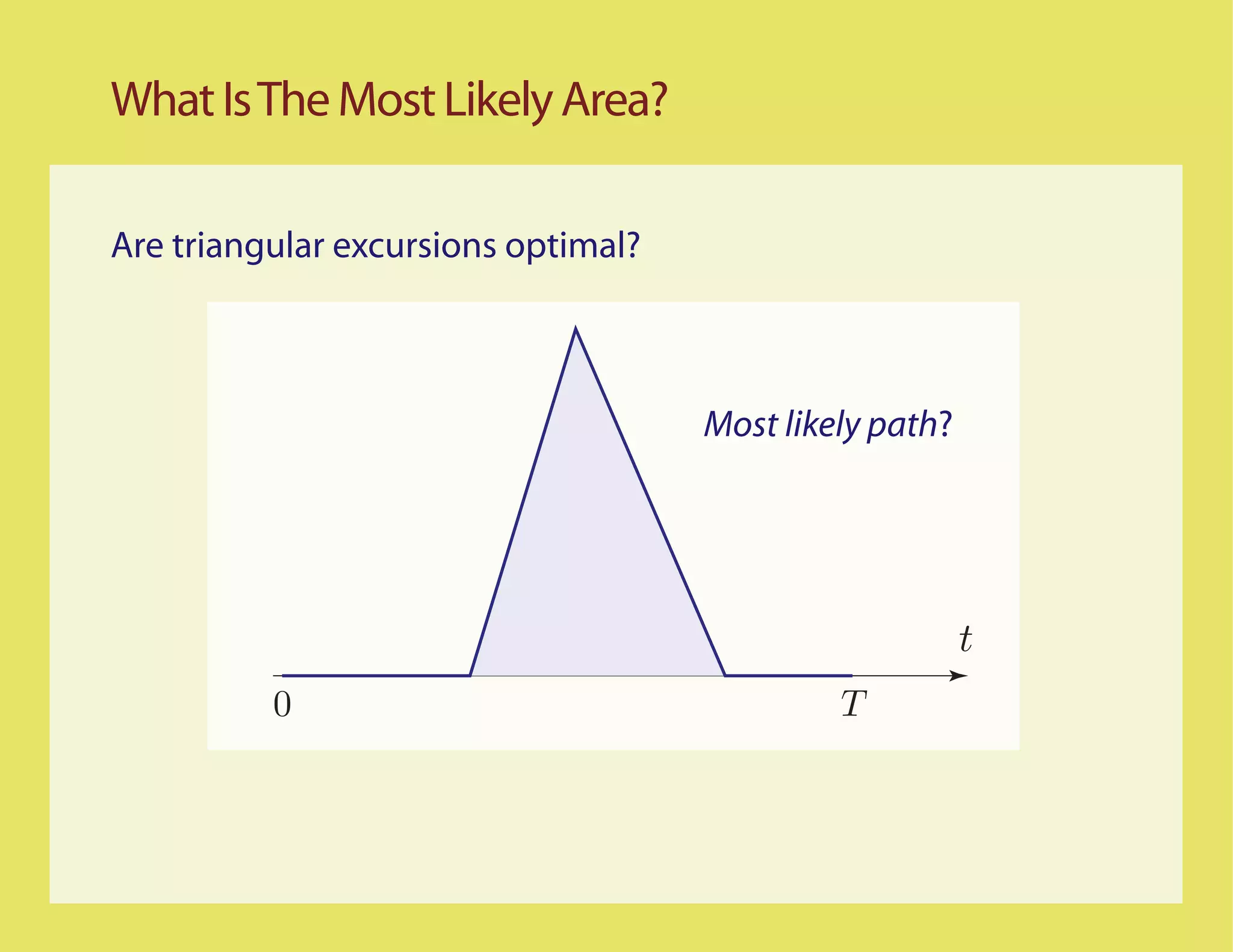
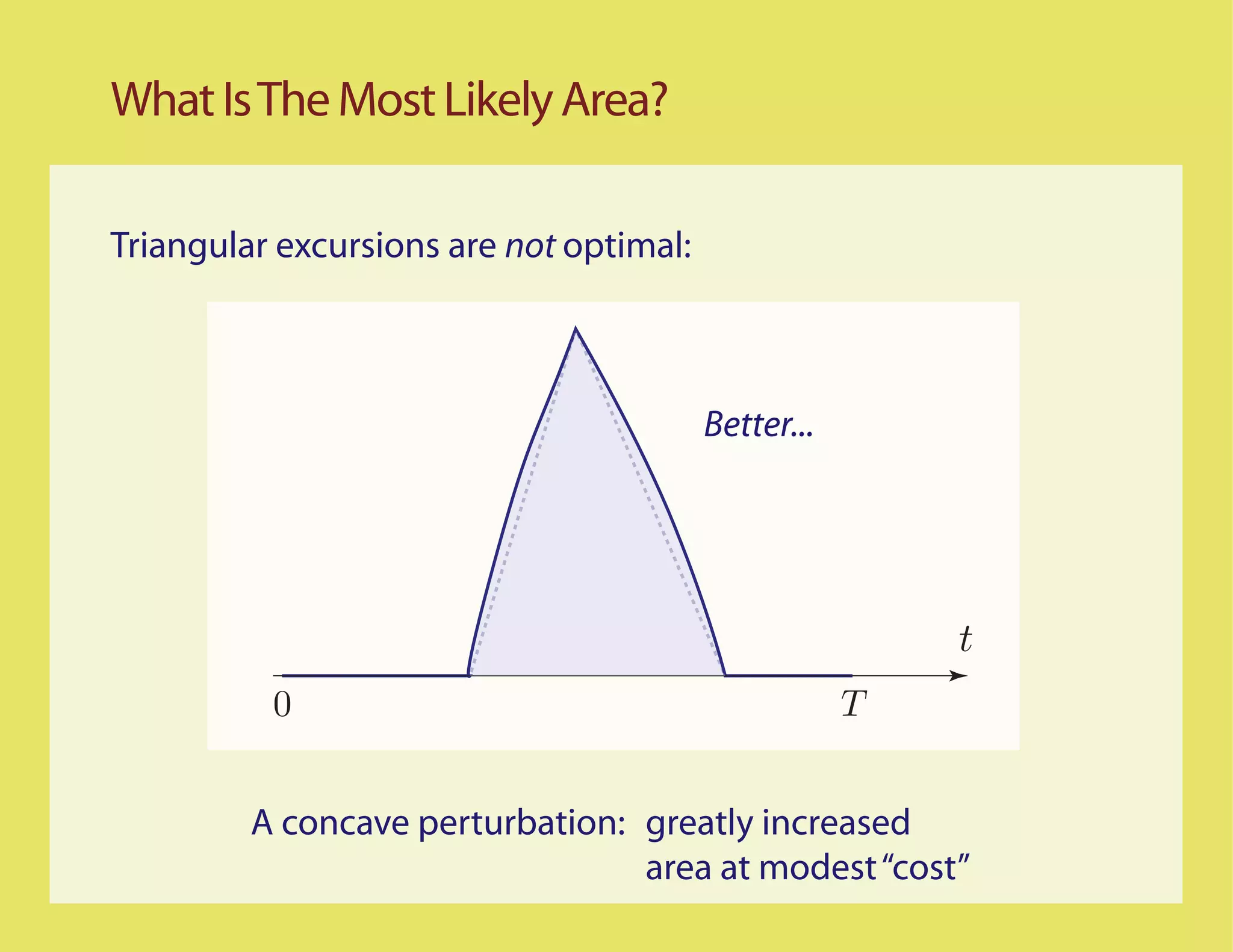
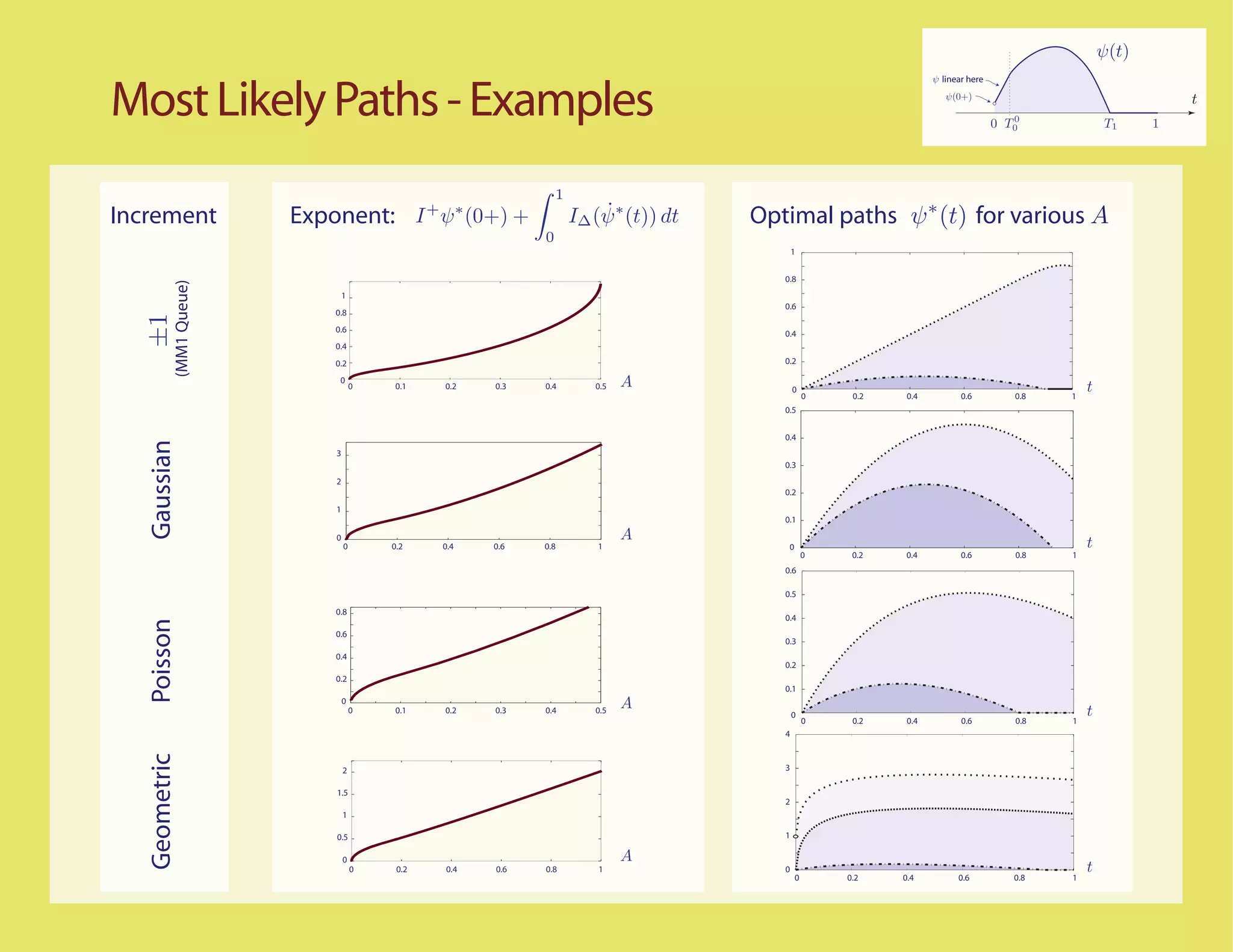
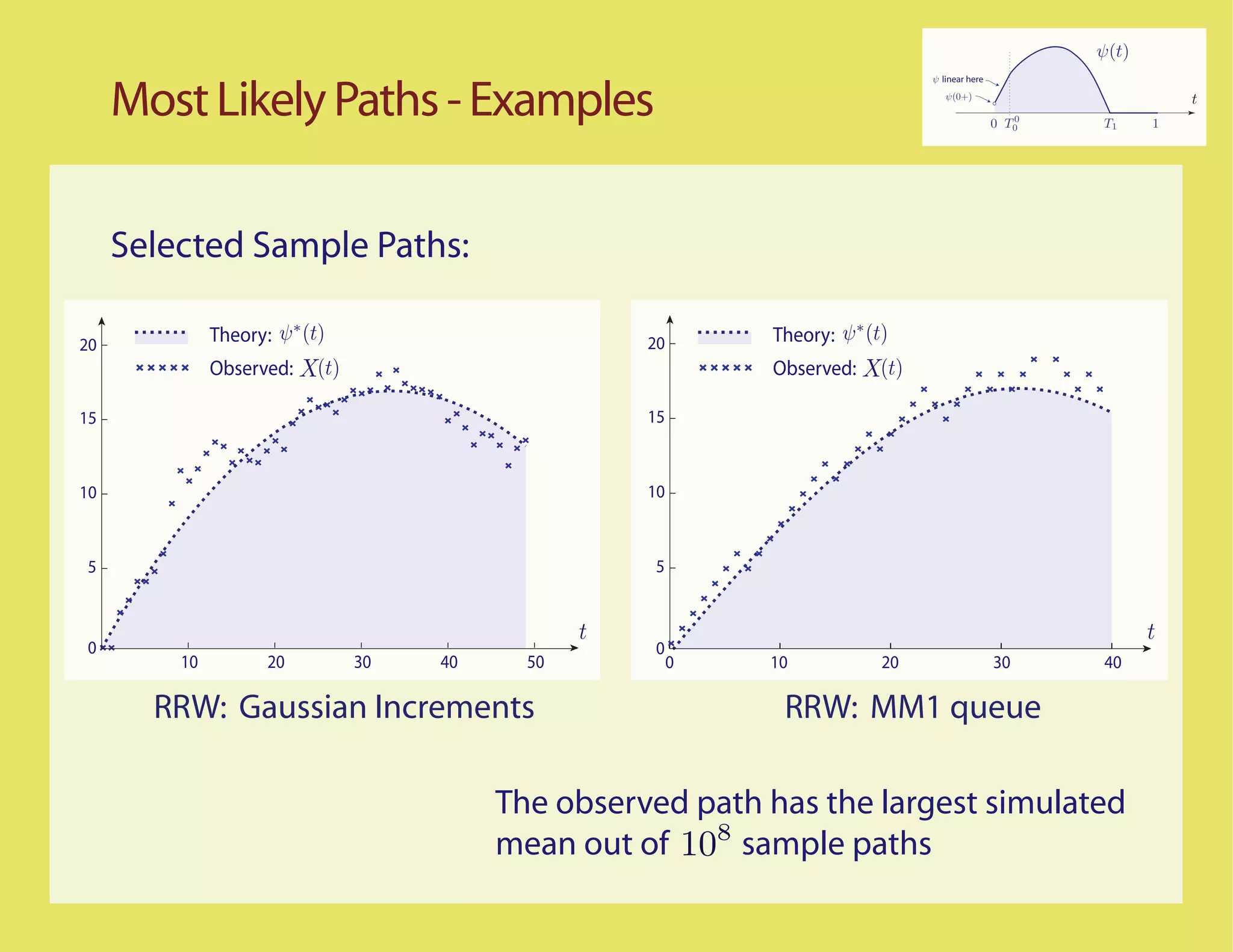
29. Better...
Most Likely Paths t
0 T
Scaled process
ψ n (t) = n−1 X(nt)
LDP question translated to the scaled process
1
η(n) ≈ An ⇐⇒ ψ n (t) dt ≈ A
0
Basic assumption: The sample paths for the unconstrained
random walk with increments ∆ satisfy the LDP in D[0,1] with
good rate function IX

30. Better...
Most Likely Paths t
0 T
Scaled process
ψ n (t) = n−1 X(nt)
LDP question translated to the scaled process
1
η(n) ≈ An ⇐⇒ ψ n (t) dt ≈ A
0
Basic assumption: The sample paths for the unconstrained
random walk with increments ∆ satisfy the LDP in D[0,1] with
good rate function IX
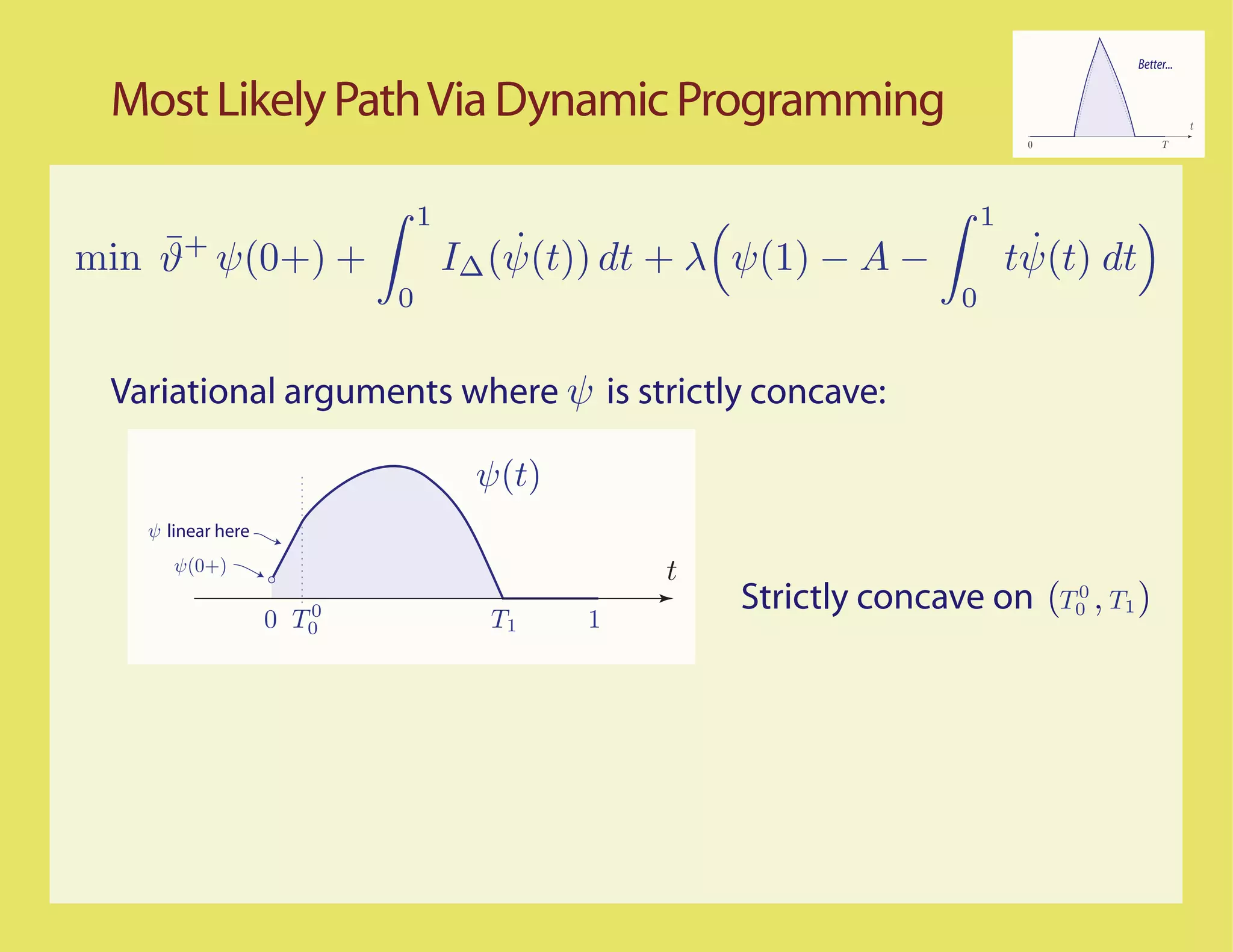
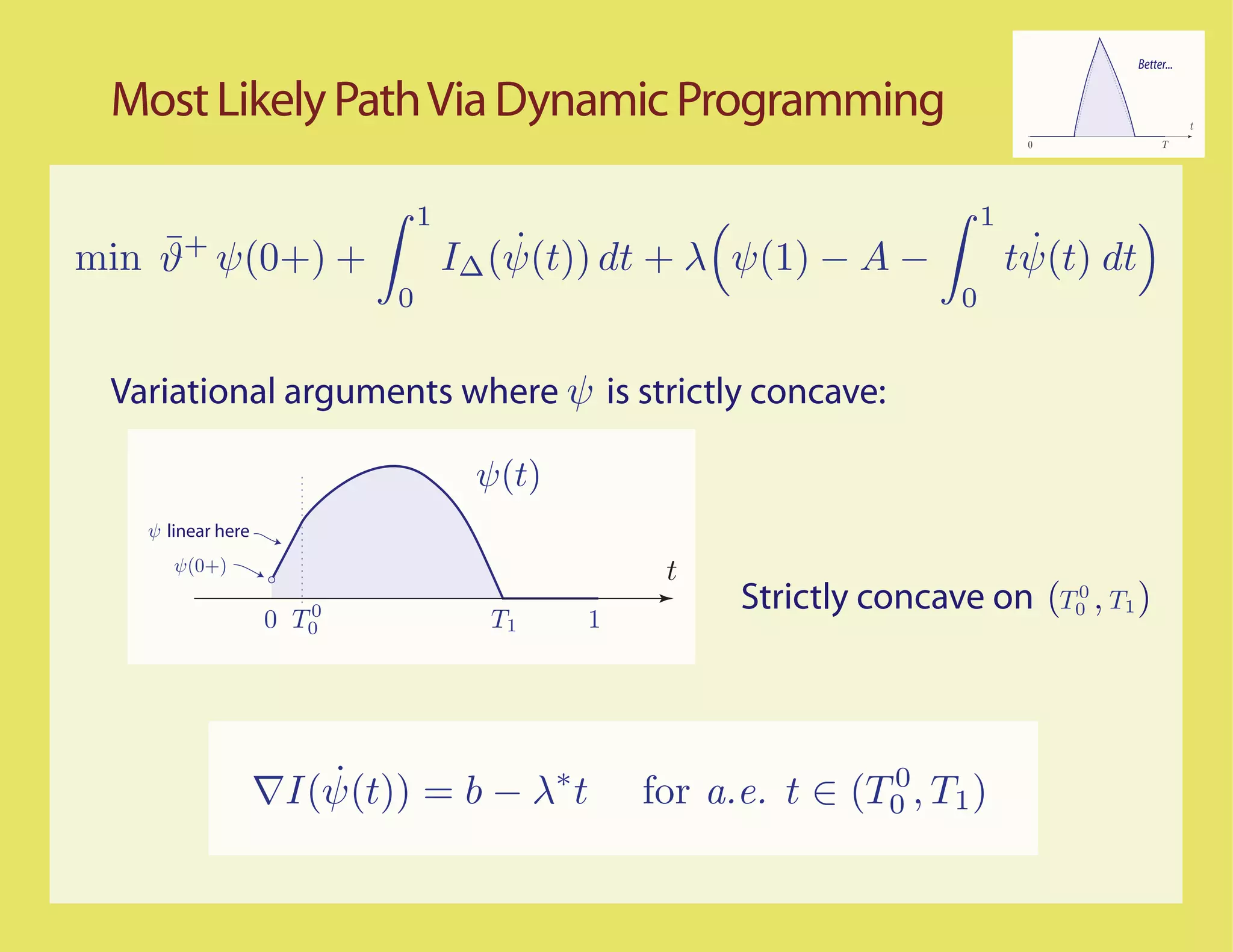
1
¯
IX (ψ) = ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt For concave ψ, with
no downward jumps
0

31. Better...
Most Likely Path Via Dynamic Programming t
0 T
Dynamic programming formulation
1
min ¯
ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt
0
1
s.t. ψ(t) dt = A
0

32. Better...
Most Likely Path Via Dynamic Programming t
0 T
Dynamic programming formulation
1
min ¯
ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt
0
1
s.t. ψ(t) dt = A
0
Solution: Integration by parts + Lagrangian relaxation:
1 1
¯
min ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt + λ ψ(1) − A − ˙
tψ(t) dt
0 0

33. Better...
Most Likely Path Via Dynamic Programming t
0 T
1 1
¯
min ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt + λ ψ(1) − A − ˙
tψ(t) dt
0 0
Variational arguments where ψ is strictly concave:
ψ(t)
ψ linear here
ψ(0+) t
0 Strictly concave on (T00 , T1 )
0 T0 T1 1

34. Better...
Most Likely Path Via Dynamic Programming t
0 T
1 1
¯
min ϑ+ ψ(0+) + ˙
I∆ (ψ(t)) dt + λ ψ(1) − A − ˙
tψ(t) dt
0 0
Variational arguments where ψ is strictly concave:
ψ(t)
ψ linear here
ψ(0+) t
0 Strictly concave on (T00 , T1 )
0 T0 T1 1
˙
I(ψ(t)) = b − λ∗ t 0
for a.e. t ∈ (T0 , T1 )

35. ψ(t)
Most Likely Paths - Examples
ψ linear here
ψ(0+) t
0
0 T0 T1 1
1
Increment Exponent: I ψ (0+) + + ∗ ˙
I∆ (ψ ∗ (t)) dt Optimal paths ψ ∗ (t) for various A
0
1
0.8
(MM1 Queue)
1
0.6
0.8
±1
0.6 0.4
0.4
0.2 0.2
0
0 0.1 0.2 0.3 0.4 0.5 A 0 t
0 0.2 0.4 0.6 0.8 1
0.5
0.4
Gaussian
3
0.3
2
0.2
1
0.1
0 A t
0 0.2 0.4 0.6 0.8 1 0
0 0.2 0.4 0.6 0.8 1
0.6
0.5
0.8
0.4
Poisson
0.6
0.3
0.4
0.2
0.2
0.1
0
0 0.1 0.2 0.3 0.4 0.5
A t
0
0 0.2 0.4 0.6 0.8 1
4
Geometric
2 3
1.5
2
1
0.5 1
0 A
0 0.2 0.4 0.6 0.8 1 0 t
0 0.2 0.4 0.6 0.8 1

36. ψ(t)
Most Likely Paths - Examples
ψ linear here
ψ(0+) t
0
0 T0 T1 1
Selected Sample Paths:
20
Theory: 20 Theory:
Observed: X Observed: X
15 15
10 10
5 5
0 0
10 20 30 40 50 0 10 20 30 40
RRW: Gaussian Increments RRW: MM1 queue
The observed path has the largest simulated
mean out of 108 sample paths

37. Conclusions

38. Summary
It is widely known that simulation variance
is high in “heavy traffic” for queueing models
Large deviation asymptotics are exotic,
regardless of load
Sample-path behavior is identified for RRW when
the sample mean is large.
This behavior is very different than previously seen
in “buffer overflow” analysis of queues

39. Summary
It is widely known that simulation variance
is high in “heavy traffic” for queueing models
Large deviation asymptotics are exotic,
regardless of load
Sample-path behavior is identified for RRW when
the sample mean is large.
This behavior is very different than previously seen
in “buffer overflow” analysis of queues
What about other Markov models?

40. MM1 queue - the nicest of Markov chains
What about other Markov models?
• Reversible
• Skip-free
• Monotone
• Marginal distribution geometric
• Geometrically ergodic

41. MM1 queue - the nicest of Markov chains
What about other Markov models?
• Reversible
• Skip-free
• Monotone
• Marginal distribution geometric
• Geometrically ergodic
The skip-free property makes
the fluid model analysis possible. Similar behavior in
• Fixed-gain SA
• Some MCMC algorithms

42. What Next?
• Heavy-tailed and/or long-memory settings?

43. What Next?
• Heavy-tailed and/or long-memory settings?
• Variance reduction, such as control variates
η(n)
30
25
η + (n)
η − (n)
20
15
10
5
n
0
0 100 200 300 400 500 600 700 800 900 1000
M 2006
CTCN

44. What Next?
• Heavy-tailed and/or long-memory settings?
• Variance reduction, such as control variates
Performance as a function of safety stocks
23 23
22 22
21 21
20 20
19 19
18 18
10 10
10 20 10 20
20 30 20 30
30 40 30 40
40
50 50 w 40
50 50 w
w 60 60 w 60 60
(i) Simulation using smoothed estimator (ii) Simulation using standard estimator
ˆ
Smoothed estimator using fluid value function in CV: g = h − P h = −Dh, h = J
Henderson, M., and Tadi´c 2003
CTCN

45. What Next?
• Heavy-tailed and/or long-memory settings?
• Variance reduction, such as control variates
• Original question? Conjecture,
1
lim √ log P η(n) ≥ r = −Jη (r) < 0, r>η
n→∞ n
for some range of r

46. [1] S. P. Meyn. Large deviation asymptotics and control variates for simulating large functions. Ann. Appl.
Probab., 16(1):310–339, 2006.
[2] S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, Cambridge, 2007.
[3] K. R. Duffy and S. P. Meyn. Most likely paths to error when estimating the mean of a reflected random
walk. http://arxiv.org/abs/0906.4514, June 2009.
References [1] I. Kontoyiannis and S. P. Meyn. Spectral theory and limit theorems for geometrically ergodic Markov
processes. Ann. Appl. Probab., 13:304–362, 2003. Presented at the INFORMS Applied Probability
Conference, NYC, July, 2001.
[2] I. Kontoyiannis and S. P. Meyn. Large deviations asymptotics and the spectral theory of multiplicatively
regular Markov processes. Electron. J. Probab., 10(3):61–123 (electronic), 2005.
[1] G. Fort, S. Meyn, E. Moulines, and P. Priouret. ODE methods for skip-free Markov chain stability with
applications to MCMC. Ann. Appl. Probab., 18(2):664–707, 2008.
[2] V. S. Borkar and S. P. Meyn. The O.D.E. method for convergence of stochastic approximation and
reinforcement learning. SIAM J. Control Optim., 38(2):447–469, 2000.
LDPs for RRW
[1] S. P. Meyn. Large deviation asymptotics and control variates for simulating large functions. Ann. Appl.
Probab., 16(1):310–339, 2006.
[2] S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, Cambridge, 2007.
[3] K. R. Duffy and S. P. Meyn. Most likely paths to error when estimating the mean of a reflected random
walk. http://arxiv.org/abs/0906.4514, June 2009.
Exact LDPs
[1] I. Kontoyiannis and S. P. Meyn. Spectral theory and limit theorems for geometrically ergodic Markov
processes. Ann. Appl. Probab., 13:304–362, 2003.
[2] I. Kontoyiannis and S. P. Meyn. Large deviations asymptotics and the spectral theory of multiplicatively
regular Markov processes. Electron. J. Probab., 10(3):61–123 (electronic), 2005.
Simulation
[1] S. G. Henderson, S. P. Meyn, and V. B. Tadi´. Performance evaluation and policy selection in multiclass
c
networks. Discrete Event Dynamic Systems: Theory and Applications, 13(1-2):149–189, 2003. Special
issue on learning, optimization and decision making (invited).
[2] S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, Cambridge, 2007.
[1] G. Fort, S. Meyn, E. Moulines, and P. Priouret. ODE methods for skip-free Markov chain stability with
applications to MCMC. Ann. Appl. Probab., 18(2):664–707, 2008.
[2] V. S. Borkar and S. P. Meyn. The ODE method for convergence of stochastic approximation and
reinforcement learning. SIAM J. Control Optim., 38(2):447–469, 2000.