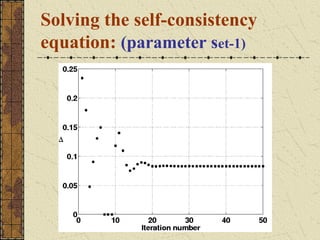
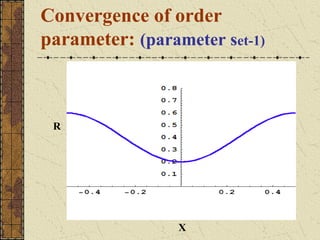
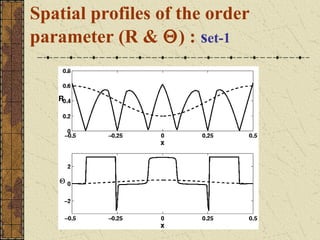
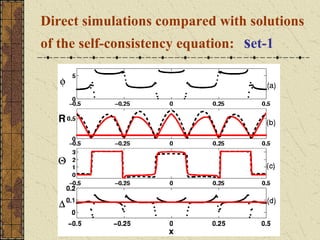
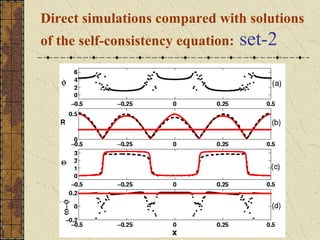
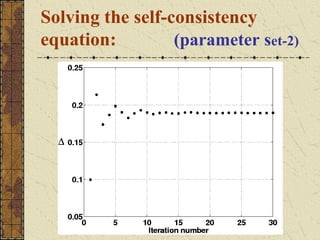
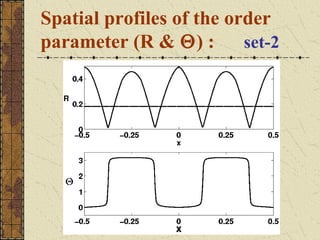
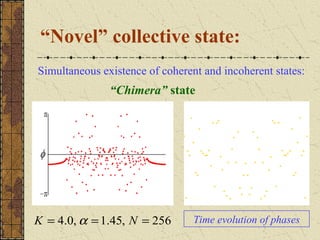
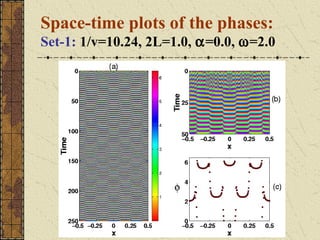
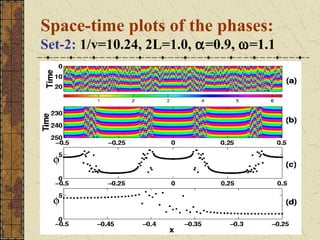
This document discusses the emergence of chimera states, a unique collective state where coherent and incoherent dynamics coexist, in a system of non-locally coupled phase oscillators with propagation delays. It presents the complex Ginzburg-Landau equation (CGLE) model of reaction-diffusion systems and derives a phase reduction with propagation time delays. Numerical simulations and solutions to the self-consistency equation validate the existence of chimera clusters induced by time delays.

1. A unique state of clustered chimera in
non-locally coupled phase oscillators
with propagation delays
Gautam C Sethia and Abhijit Sen
Institute for Plasma Research
Bhat, Gandhinagar 382 428, India
Fatihcan M Atay
Max Planck Institute for Mathematics in the Sciences
Leipzig 041103, Germany

2. Reaction-diffusion systems:
Kuramoto starts his famous book
“Chemical Oscillations, Waves
and Turbulence” with the words:
“Mathematically, a reaction-
diffusion system is obtained by
adding some diffusion terms to
a set of ordinary differential
equations which are first-order
in time.”

3. Normal form of bifurcation:
Like in case of a single oscillator, it is possible
to derive the normal form at the supercritical
Hopf bifurcation point for spatially extended
systems with diffusive coupling. The result is
well known and well studied complex
Ginzburg-Landau equation (CGLE) which
describes the universal dynamics of reaction-
diffusion systems close to the emergence of
uniform oscillations.

4. Complex Ginzburg-Landau
Equation (CGLE):
One-dimensional CGLE:
∂ 2 ∂2
A( x, t ) = A − (1 + iC2 ) A A + (1 + iC1 ) 2 A( x, t )
∂t ∂x
Discrete version of CGLE is as follows:
2
∂ t Ai = Ai − (1 + iC2 ) Ai Ai + (1 + iC1 )( Ai −1 − 2 Ai + Ai +1 )
Limit cycle oscillator Diffusive coupling
A(t ) = ρe iωt
ρ = 1, ω = −C2

5. Collective modes of coupled
oscillators:
• Coherent solutions of the CGLE correspond to collective
modes of a large assembly of coupled oscillators
• A variety of solutions exist:
• plane waves
• hole solutions
• fronts
• spirals (in 2D)
• scrolls (in 3D)
• Wide applications in a variety of physical, chemical and
biological systems

6. Non-local CGLE:
∂ 2
A( x, t ) = A − (1 + iC2 ) A A + K (1 + iC1 )( Z ( x,t ) − A( x, t ))
∂t
Z ( x, t ) = ∫ G ( x − x' ) A( x' , t )dx'
κ ( −κ y )
G( y) = e
2
Important in many physical, chemical, biological modeling:
• interaction between neurons over large distances
• certain reaction diffusion systems for chemical
interactions
• heat pulse propagation problems in tokamak plasmas
• Josephson junction arrays

7. Coexistence of coherence and
incoherence:
Solving the non-locally coupled CGLE for a
finite system size with periodic boundary
conditions and in a suitable range of
parameters, in which the uniform oscillation is
linearly stable, the system develops peculiar
patterns of coexisting coherence and
incoherence named as chimera.

8. “Novel” collective state:
Simultaneous existence of coherent and incoherent states:
“Chimera” state
K = 4.0, α = 1.45, N = 256 Time evolution of phases

9. Chimera in greek mythology:
The three-formed
monster Khimaira
(chimera) is depicted
with a lion's body
and head, a goat's
drooping udders and
goat-head rising
from the middle of
its back, and a
serpent-headed tail.

10. Chimera in the present
context:
A mathematical Chimera in which an array of
identical oscillators splits into two domains: one
coherent (phase locked) and the other incoherent
(desynchronized).
First identified by Kuramoto and Battogtokh
(Nonl. Phenom. Compl. Syst. 5, 380, 2002) and
named Chimera by Abrams and Strogatz (Phys.
Rev. Lett. 93, 174102, 2004).

11. Can a chimera state exist in a time
delayed system?
• Time delay arises due to finite propagation
speed of a signal.
• Information arises later and later from
distant oscillators to a given oscillator –
model assumes constant speed v of signals.

12. The phase reduction of non-
locally coupled CGLE:
When the coupling strength K is weak, the
non-locally coupled CGLE takes the form :
∂φ
= ω − ∫ G ( x − x' ) sin[φ ( x, t ) − φ ( x' , t ) + α ]dx'
∂t
C 2 − C1
tan(α ) = , α (C 2 − C1 ) > 0
1 + C1C 2

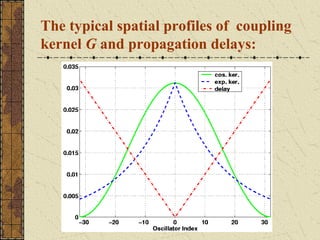
13. Phase equation with
propagation time delays:
∂φ x − x'
= ω − ∫ G ( x − x' ) sin[φ ( x, t ) − φ ( x' , t − ) + α ]dx'
∂t v
κ
G ( y ) = exp(−κ y ) Exponential kernel
2
∫ G( y)dy = 1
v is the propagation velocity

14. The typical spatial profiles of coupling
kernel G and propagation delays:

15. Space-time plots of the phases:
Set-1: 1/v=10.24, 2L=1.0, α=0.0, ω=2.0

16. Chimera states with and without
delay: (parameter set-1)
With delay Without delay

17. Space-time plots of the phases:
Set-2: 1/v=10.24, 2L=1.0, α=0.9, ω=1.1

18. Phase equation with relative
phases:
The phase equation can be rewritten in
terms of the relative phases
θ(x,t)=φ(x,t)-Ωt :
∂θ x − x' x − x'
= ω − Ω − ∫ G ( x − x' ) sin[θ ( x, t ) − θ ( x' , t − ) +α + Ω ]dx'
∂t v v
where Ω denotes a constant drift frequency.

19. Complex order parameter for
time delayed system:
 x− x' x− x' 
i θ ( x ',t − ) −Ω 
R ( x , t ) e iΘ ( x , t ) = ∫ G ( x − x ' ) e 
 v v 

dx'
∂θ
= ω − Ω − R sin[θ − Θ + α ]
∂t
θ = φ − Ωt , ∆ = ω − Ω
R( x) ≥ ∆ phase − locked solutions
R( x) < ∆ phase − drift solutions

20. Self-consistency equation with time
delays for stationary solutions:
Under the restriction of stationary solutions, in
which R and Θ depend on space but not on
time, the following self-consistency equation
is obtained:
 x− x' 
i  Θ ( x ') − Ω   ∆ − ∆2 − R 2 ( x' ) 
R ( x ) e iΘ ( x ) = e iβ ∫ G ( x − x ' ) e  v 
 
  dx'
 R( x' ) 
 
π
β = −α
2
∆ =ω −Ω

21. Solving the self-consistency
equation: (parameter set-1)

22. Convergence of order
parameter: (parameter set-1)
R
X

23. Spatial profiles of the order
parameter (R & Θ) : set-1

24. Direct simulations compared with solutions
of the self-consistency equation: set-1

25. Direct simulations compared with solutions
of the self-consistency equation: set-2

26. Conclusions:
Nonlocal coupling is not simply an intermediate
coupling between “local” and “global” but
generates a wide range of unexpected behaviour
and the chimera state is one of them.
The propagation delays further restructure the no-
delay chimera state into a periodic cluster of anti-
phase coherent regions interspersed by incoherent
regions.

27. Conclusions: contd.
Our numerical simulations of the coupled oscillator
dynamics are further validated and explained
through the solutions of a generalized functional
self-consistency equation of the mean field.
Thus time delay offers an additional mechanism for
cluster formations in dynamical systems and model
systems incorporating time delays may provide a
useful paradigm for studying this phenomenon.

28. Conclusions: contd.
The number and the distribution of the clusters is a
sensitive function of delay and is a result of time
delay induced spatial modulations of the order
parameter R.
There is a correspondence between the number of
clusters (2q) and the wave number (q) of the co-
existing traveling wave solutions.
The work is under progress to investigate the
phase-locked and the chimera states in a wide
range of system parameters and delay values.

29. Pegasus, used in the battle
against Chimera:
Thank you very
much for your
attention.
Mythological figures have been obtained from the
site http://www.theoi.com (Theoi project: Guide to
Greek mythology).

30. Solving the self-consistency
equation: (parameter set-2)

31. Spatial profiles of the order
parameter (R & Θ) : set-2

32. Reaction-diffusion systems:
Kuramoto starts his famous book “Chemical Oscillations,
Waves and Turbulence” with the words:
“Mathematically, a reaction-diffusion system is obtained by
adding some diffusion terms to a set of ordinary differential
equations which are first-order in time.”
Like in case of a single oscillator, it is possible to derive the
normal form at the supercritical Hopf bifurcation point for
spatially extended systems with diffusive coupling. The result is
well known and well studied complex Ginzburg-Landau
equation (CGLE) which describes the universal dynamics of
reaction-diffusion systems close to the emergence of uniform
oscillations.