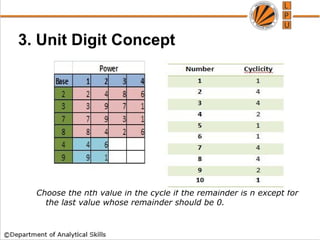
This document discusses various topics related to numbers including: 1) Classification of numbers and converting decimals to fractions through examples such as converting 6.424242 to 636/99. 2) Power cycles and unit digits, explaining concepts like finding the unit digit of expressions through examples. 3) Factors and multiples, covering topics like finding the number of factors of a number and the sum of factors through examples. 4) Factorials and finding the maximum power of a prime number in a factorial. 5) Divisibility rules and the remainder theorem, exemplified through practice questions.

1. PEA-210–Lecture#
NUMBERS

2. Content
Content
 CLASSIFICATION OF NUMBERS
ii) Conversion of a decimal number to fraction
 POWER CYCLE/ UNIT DIGIT
 FACTORS AND MULTIPLES
i) Number of factors
ii) Sum of factors
iii) Product of factors

3. How to find whether a no is Prime or not
Conversion of a decimal number to fraction:
Example: 6.424242.........
Let x = 6.424242....
100x = 642.424242.....
(100x – x)= (642.424242.... – 6.424242.....)
99x = 636
x = 636/99
∴ 6.424242...... = 636/99
Example: 0. 3 = 3/9 = 1/3
0.63 = 63/99 = 7/11
0.1 56 = 156 -1/990 = 155/990 = 31/198
0.7 3 = 73-7/90 = 66/90 = 11/15

4. Q. Convert 3.33333333…..
Q. Convert 2.3535353535……
Q. Convert 5.26777777….
How to find whether a no is Prime or not

5. Choose the nth value in the cycle if the remainder is n except for
the last value whose remainder should be 0.
3. Unit Digit Concept

7. How to find whether a no is Prime or not
Note: The last digit of an expression will always depend on the unit digit of the
values.
Example: The unit digit of 123 x 456 x 789 = 3 x 6 x 9
= 18 x 9
= 8 x 9
= 2

8. How to find whether a no is Prime or not
Example 2: What is the unit digit of (123)^42?
The unit digit pattern of 3 repeats four times. So find the remainder when the
power value is divided by 4.
42/4= R(2)
2nd
value in 3 cycle is 9.
∴ Unit digit of (123)^42 is 9
Example 3: Find the units place digit of 252^84?
Consider only unit digit of a number i.e. 2^84
84/4 = 0 (Remainder)
So, power of 2 will become its Cyclicity i.e. 4.
Therefore, Unit digit of 24 = 6.

9. Q) What is the unit digit of (127)^223
Q) What is the unit digit in the product (3^65 x 6^59 x 7^71)?
Q) Find the units place digit of 27^184?

10. 4. Factors
 Factors of a number are the values that divides the number
completely.
Example: Factors of 10 are 1, 2, 5 and 10.
 Multiple of a number is the product of that number and any
other whole number.
Example: multiples of 10 are 10, 20, 30,…..

11. Number of factors
Example: Find total number of factors of 3600?
OR
Find all the numbers which can divide 3600?
Sol:
Step 1: Prime factorize the given number
3600 = 36 x 100
= 6^2 x 10^2
= 2^2 x 3^2 x 2^2 x 5^2
= 2^4 x 3^2 x 5^2
Step 2: Add 1 to the powers and multiply.
(4+1) x (2+1) x (2+1)
= 5 x 3 x 3
= 45
∴ Number of factors of 3600 is 45.

12. Q) Find the number of factors of 14400?

13. Sum of factors
Example: 45
Step 1: Prime factorize the given number
45 = 3^2 x 5^1
Step 2: Split each prime factor as sum of every distinct
factors.
(3^0 + 3^1 + 3^2) x (5^0 + 5^1)
The following result will be the sum of the factors
= 78

15. 6. FACTORIAL
 6! = 1 * 2 * 3 * 4 * 5 * 6 = 720
n! = 1 when n = 0, and n! = (n-1)! * n if n > 0
 The highest power of prime number p in n!
= [n/p1] + [n/p2] + [n/p3] + [n/p4] + …..
where [n/p1] denotes the quotient when n is divided by p
Example: The maximum power of 5 in 60!
60! = 1 x 2 x 3 ..................60 so every fifth number is a multiple of 5. So
there must be 60/5 = 12
In addition to this 25 and 50 contribute another two 5's. so total number is
12 + 2 = 14
Short cut: [60/5]+[60/25]=12+2=14

16. Q. How many zeros are there in 100!?

17. Find the number of zeroes at the end of the
product 35 x 36 x 37 x….x 89 x 90

18. Find the number of zeroes at the end of the
product 41 x 42 x….x 109 x 110

19. Divisibility Rules
Divisibility Rules

20. Question: If number 1792N is divisible by 2. How many values
N can take?
[A] 4
[B] 5
[C] 3
[D] 6

21. Question: What should come in place of K if 563K5 is divisible
by 9?
[A] 7
[B] 8
[C] 9
[D] 2

22. Question: For what values of P number 345472P34 is exactly
divisible by 9.
[A] 3
[B] 4
[C] 6
[D] 7

23. Question: For what values of N number 9724N is exactly
divisible by 6.
[A] 2 & 8
[B] 4 & 6
[C] 2 & 6
[D] 6 & 8

24. Question: For what values of N number 857N32 is exactly
divisible by 11.
[A] 1
[B] 0
[C] 3
[D] 4

25. Question: What should come in place x if 4857x is divisible by
88?
[A] 6
[B] 8
[C] 2
[D] 4

26. Remainder theorem
Dividend= (Divisor × Quotient + remainder)

27. Q) Remainder when 17^23 is divided by 16?
[A] 1
[B] 2
[C] 3
[D] 4

28. Q) Remainder when 35^113 is divided by 9?
[A] 1
[B] 8
[C] 3
[D] 4

29. Q) Remainder when 2^33 is divided by 9?
[A] 1
[B] 4
[C] 8
[D] 5

30. Next Class HCF & LCM