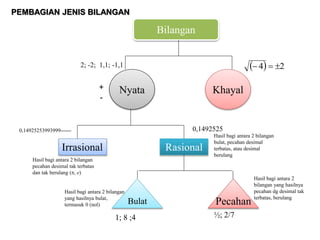
Dokumen ini menjelaskan tentang sistem bilangan dalam matematika ekonomi, termasuk bilangan nyata, khayal, dan operasi bilangan seperti penjumlahan, pengurangan, perkalian, dan pembagian. Ditekankan juga tentang kaidah perbandingan, sifat-sifat operasi bilangan, dan teknik pemadanan untuk operasi pecahan. Selain itu, terdapat penjelasan mengenai tanda ketidaksamaan dan aplikasinya dalam perhitungan.

1. SISTEM BILANGAN
MATEMATIKA EKONOMI

2. Bilangan
Nyata Khayal
Irrasional Rasional
Bulat Pecahan
2; -2; 1,1; -1,1   2
4 


0,14925253993999------ 0,1492525
1; 8 ;4 ½; 2/7
+
-
Hasil bagi antara 2 bilangan
bulat, pecahan desimal
terbatas, atau desimal
berulang
Hasil bagi antara 2 bilangan
pecahan desimal tak terbatas
dan tak berulang (, e)
Hasil bagi antara 2 bilangan
yang hasilnya bulat,
termasuk 0 (nol)
Hasil bagi antara 2
bilangan yang hasilnya
pecahan dg desimal tak
terbatas, berulang
PEMBAGIAN JENIS BILANGAN

3. Hubungan perbandingan antar bilangan
• Tanda < melambangkan “lebih kecil dari”
• Tanda > melambangkan “lebih besar dari”
• Tanda < melambangkan “lebih kecil dari atau sama dengan”
• Tanda > melambangkan “lebih besar dari atau sama dengan”
Tanda Ketidaksamaan
1. Jika a < b, maka –a > -b
2. Jika a < b dan x > 0, maka x.a < x.b
3. Jika a < b dan x < 0, maka x.a > x.b
4. Jika a < b dan c < d, maka a+c < b+d
Sifat Perbandingan

4. Operasi Bilangan
1. Kaidah Komutatif
a + b = b + a
a x b = b x a
2. Kaidah Asosiatif
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c)
3. Kaidah Pembatalan
a + c = b + c
Maka : a = b
a x c = b x c
Maka : a = b

5. 4. Kaidah Distributif
a (b + c) = ab + ac
5. Unsur Penyama
a + 0 = a
a x 1 = a a : 1 = a
6. Kebalikan
a x 0 = 0
a x 1/a = 1

6. Operasi Tanda
• Operasi Penjumlahan
a. (+ a) + (+b) = (+c)
b. (- a) + (- b) = (- c)
c. (+ a) + (- b) = (+ c) jika |a| > |b|
(+ a) + (- b) = (- d) jika |a| < |b|
d. (- a) + (+ b) = (+ c) jika |a| < |b|
(- a) + (+ b) = (- d) jika |a| > |b|

7. Operasi Tanda
• Operasi Pengurangan
a. (+ a) - (+ b) = (+ c) jika |a| > |b|
(+ a) - (+ b) = (- d) jika |a| < |b|
b. (- a) - (- b) = (+ c) jika |a| < |b|
(- a) - (- b) = (- d) jika |a| > |b|
c. (+ a) - (- b) = (+ c)
d. (- a) - (+ b) = (- c)

8. Operasi Tanda
• Operasi Perkalian
(+ a) x (+ b) = (+ c) (- a) x (- b) = (+ c)
(+ a) x (- b) = (- c) (- a) x (+ b) = (- c)
• Operasi Pembagian
(+ a) : (+ b) = (+ c) (- a) : (- b) = (+ c)
(+ a) : (- b) = (- c) (- a) : (+ b) = (- c)

9. Operasi Bilangan Pecahan
• Operasi Pemadanan
• Operasi Penjumlahan dan Pengurangan
• Operasi Perkalian
• Operasi Pembagian

10. Operasi Pemadanan
:
:
x
x
c
b
c
a
b
a
c
b
c
a
b
a


Operasi Penjumlahan dan Pengurangan
Dua buah pecahan atau lebih, hanya dapat ditambahkan
atau dikurangkan apabila mereka memiliki suku pembagi
yang sama atau sejenis. Jika suku pembaginya belum
sama, maka terlebih dahulu harus disamakan sebelum
pecahan-pecahan tersebut ditambahkan dan dikurangkan.

11. Operasi Perkalian
Operasi Pembagian
xy
ab
y
b
x
a


xb
ay
b
y
x
a
y
b
x
a



:

12. Latihan
6
1
:
7
2
:
4
3
)
(
6
1
7
2
4
3
)
(
6
1
7
2
4
3
)
(
6
1
7
2
4
3
)
(
:
d
c
b
a
Selesaikan





