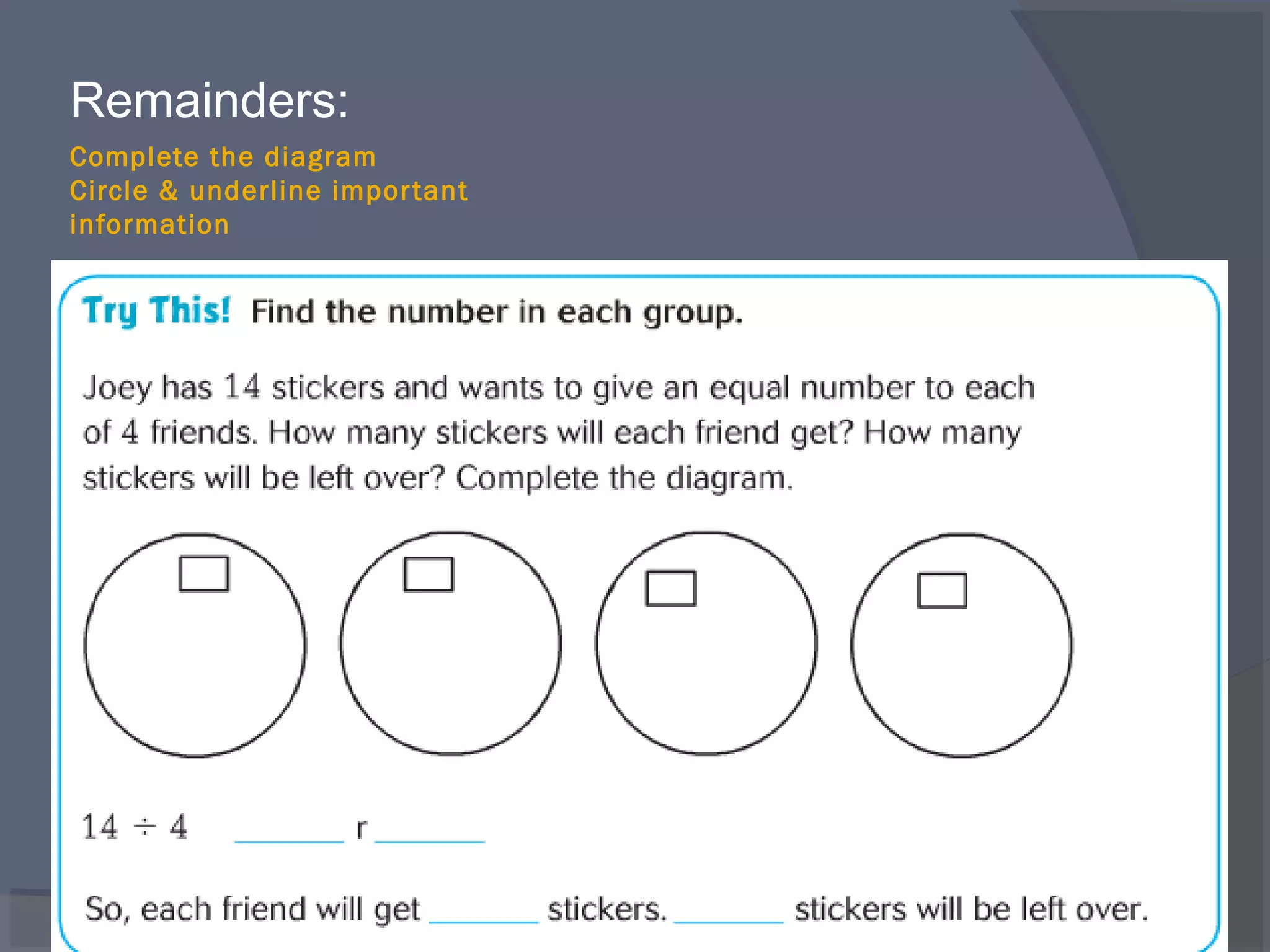
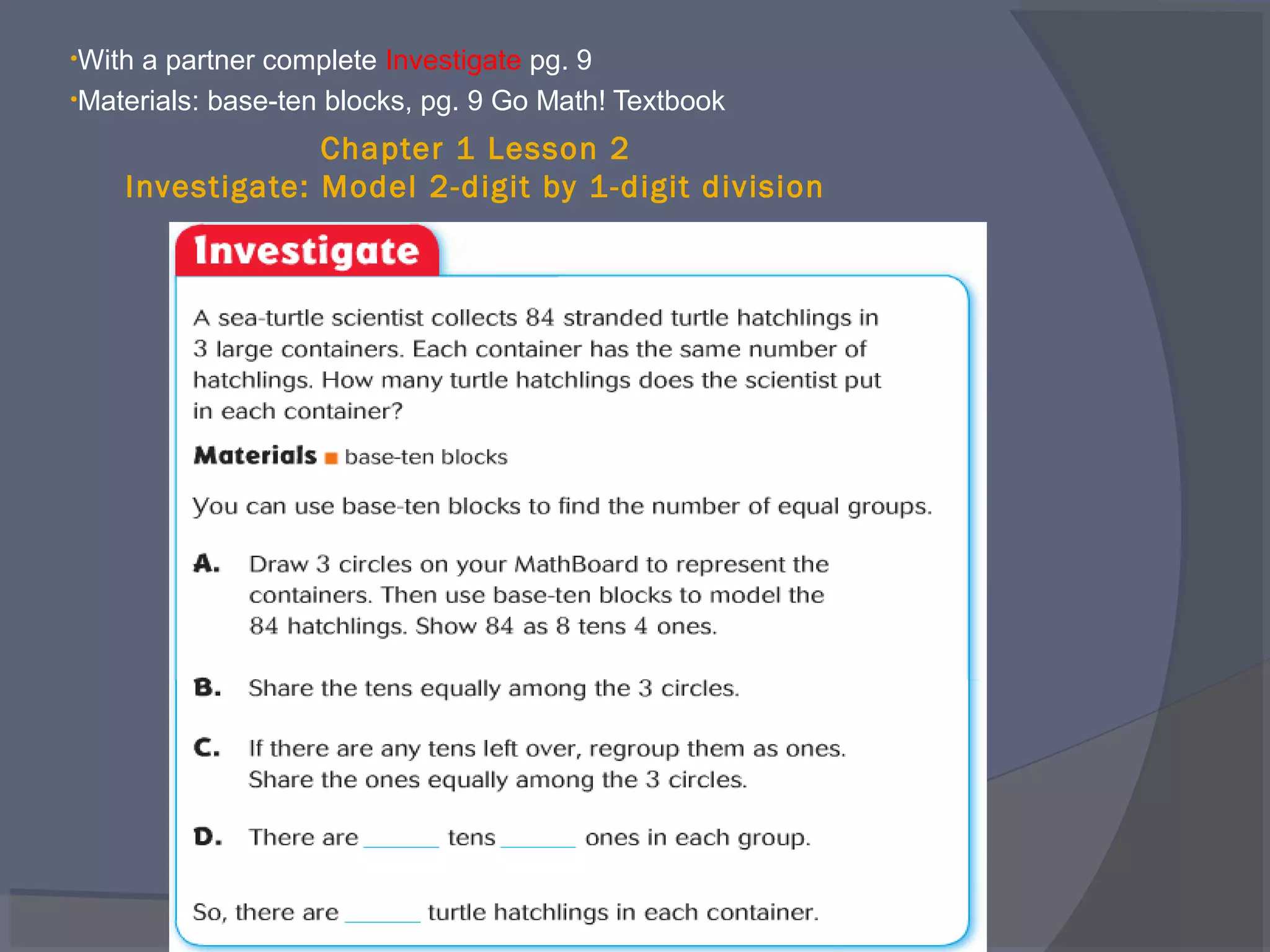
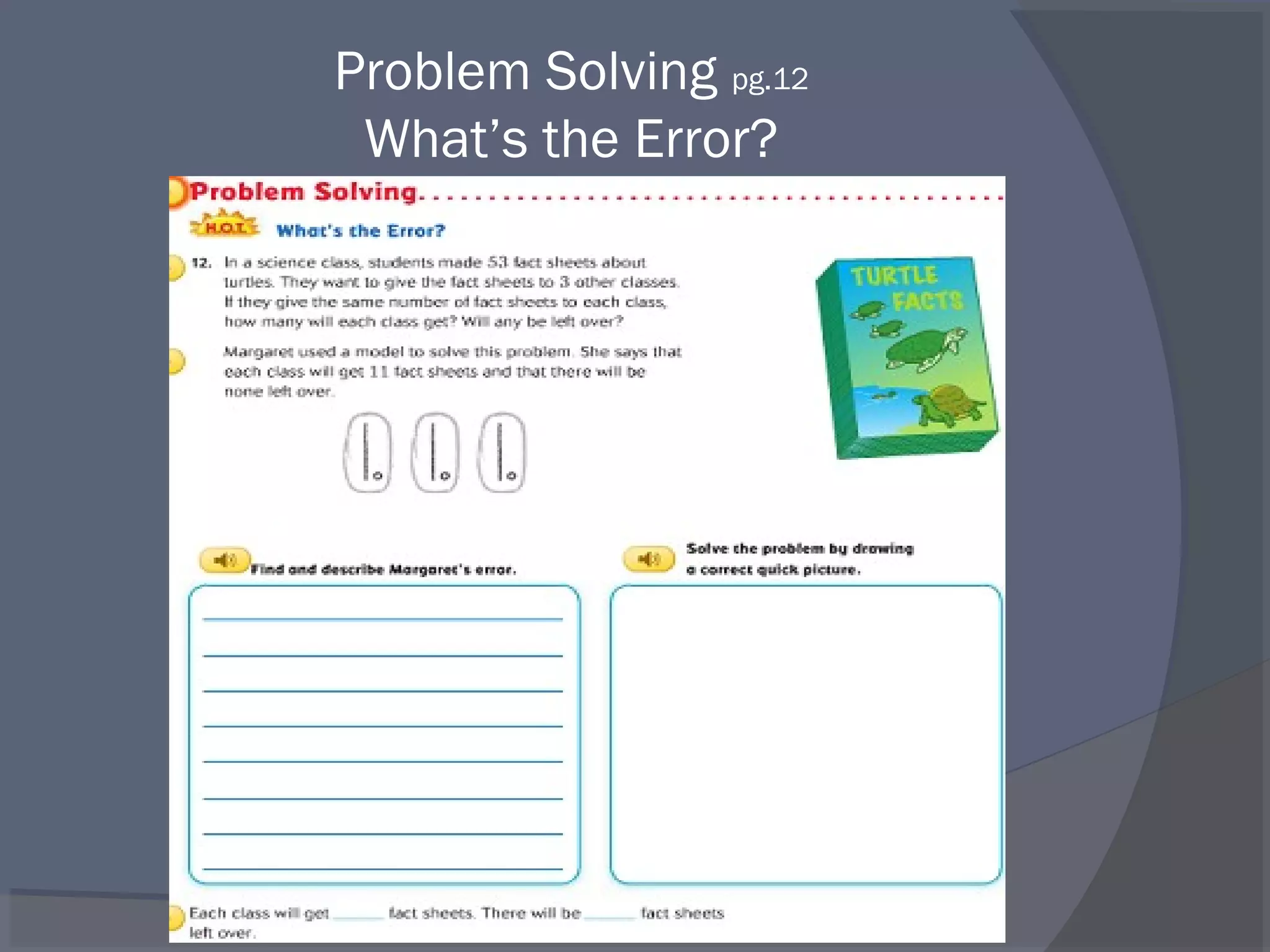
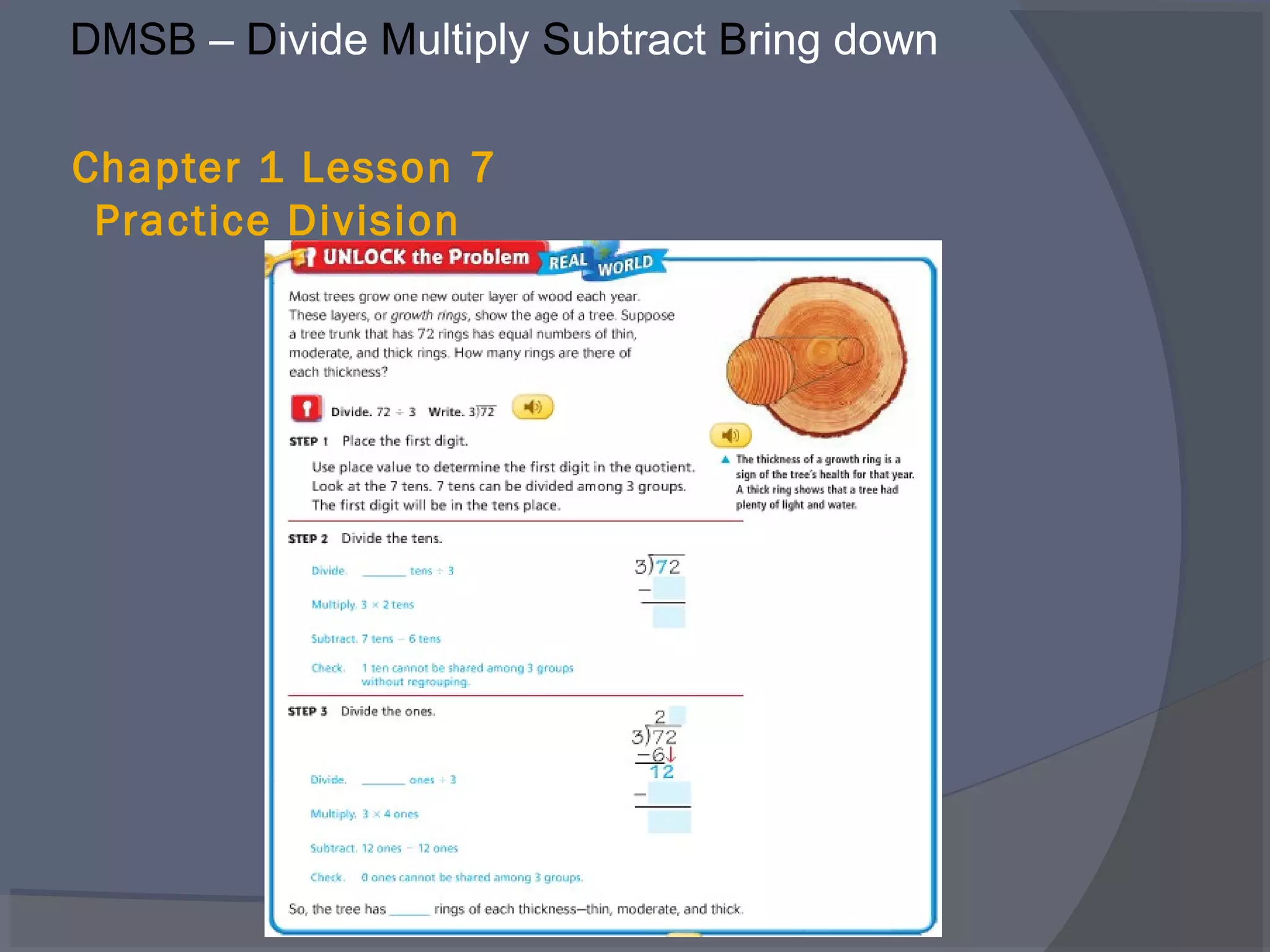
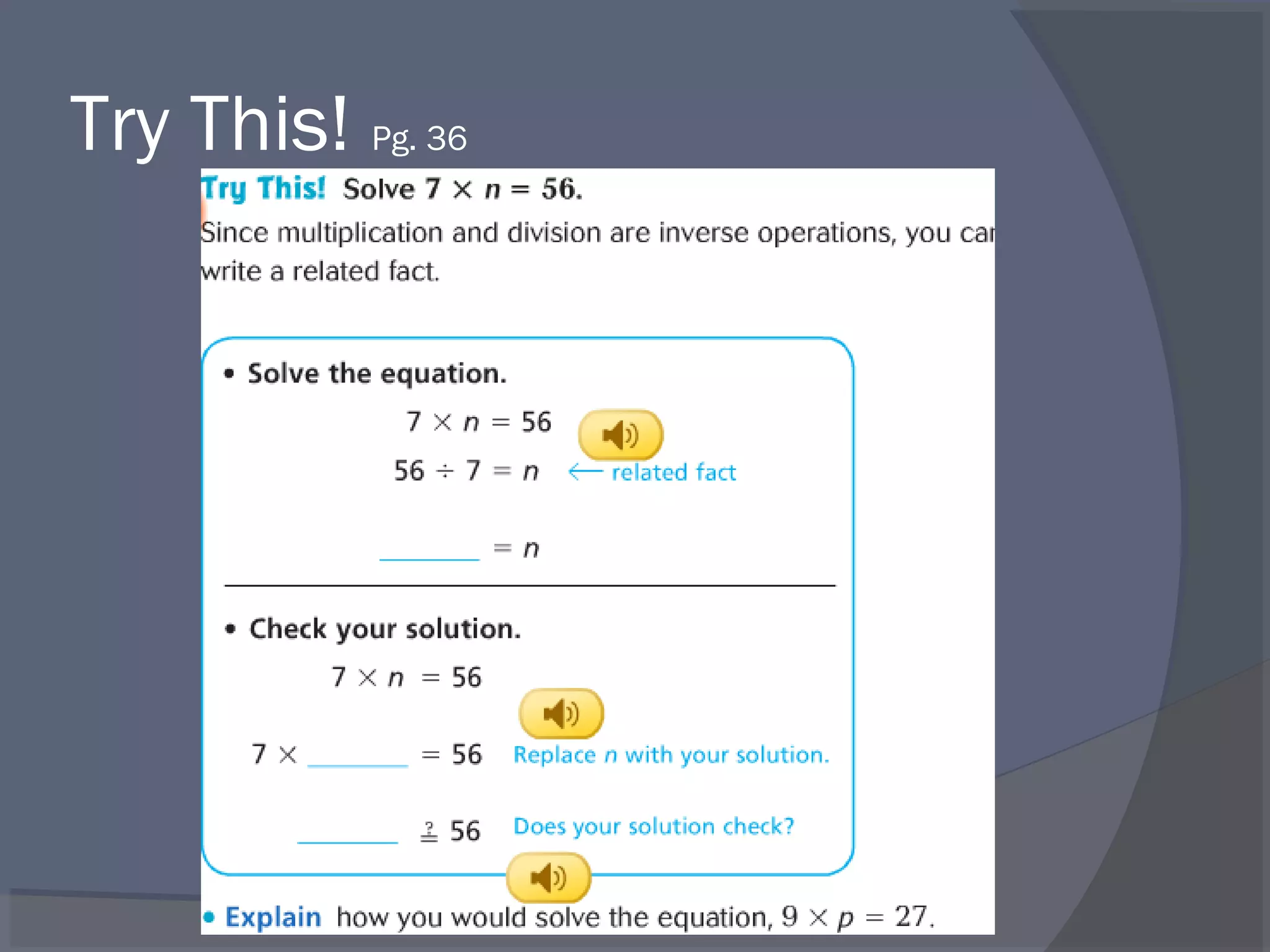
The document defines key vocabulary terms related to division, including: dividend, divisor, quotient, remainder, inverse operations, and distributive property. It also discusses different methods for solving division problems, such as using visual models, the partial quotients algorithm, and estimating quotients through mental math strategies like the distributive property. The purpose is to introduce foundational division concepts and procedures.

2. Chapter 1: Vocabulary Words
 Divide - To separate into equal groups; the opposite
operation of multiplication
 Dividend – Total amount ~ the number being divided in a
division problem
 Example: 500 ÷ 10 = 50
 Divisor – The number that divides the dividend ~
number of equal groups or number in each group
 Example: 500 ÷ 10 = 50
 Quotient – The answer to a division problem (not including
the remainder)
 Example: 500 ÷ 10 = 50

3. Vocabulary continued
 Equation – uses an equal sign to show that two
amounts are equal
 Inverse Operations – operations that undo one
another
 Example: multiplication & division; addition & subtraction
 Variable – a letter or symbol that stands for one or more
numbers
 Remainder – the amount left over when a number cannot be
divided equally
 Example: 501 ÷ 10 = 50 r1

4. Vocabulary continued
 Distributive Property - The property that
states that multiplying a sum by a
number is the same as multiplying each
addend by the number and then adding
the products
 Partial Quotients - A method of dividing
in which multiples of the divisor are
subtracted from the dividend and then
the quotients are added together.

5. Chapter 1 Lesson 1
Division Concepts

6. Remainders:
Complete the diagram
Circle & underline impor tant
information

7. Problem Solving pg.8
Draw a picture to solve.
14. Lindsey took 40 photos. She wants to
arrange her photos in a scrapbook, with
5 photos on each page. How many
pages will Lindsey need? How many
photos will Lindsey have left over?

8. Draw a picture to solve
15. Grace arranges 20 field trip photos
equally on 4 pages. Dan arranges 18
photos equally on 3 pages. Who has
more field trip photos on a page?

9. Write Math – Journal
When you divide, how do you know if
you are finding the number in each
equal group or the number of equal
groups?

10. •Witha partner complete Investigate pg. 9
•Materials: base-ten blocks, pg. 9 Go Math! Textbook
Chapter 1 Lesson 2
Investigate: Model 2-digit by 1-digit division

11. Model Division & Draw a Quick Picture
 Connect pg. 10
Five types of turtles live in Florida’s waters. They are
the green turtle, the hawksbill, the Kemp’s ridley, the
leatherback, and the loggerhead.
Suppose there are 63 rescued sea turtles. They are
divided equally among 4 large tanks. Any turtles left
over are put in a small tank. How many turtles are in
each large tank? How many are in the small tank?
Use the base-ten blocks to solve.
Then draw a quick picture.
There are _____ sea turtles in each of the 4 tanks and
____ sea turtles in the small tank.

12. Problem Solving pg.12
What’s the Error?

13. Write Math - Journal
How can you use base-ten blocks to
model and understand how to divide
whole numbers?

14. Chapter 1 Lesson 4
Solve a Simpler Problem
Division & Multiplication
 Use multiples of the divisor to help you solve a simpler
problem.
 Mark works in an animal shelter. To feed 6
dogs, Mark empties seven 12-ounce cans of
dog food into a large bowl. If he divides the
food equally among the dogs, how many
ounces of food will each dog get?
 What multiples of 6 add up to 84?

15. Solve a simpler problem
84 ÷ 6
(60 + 24) ÷ 6
Now you are going divide each of the addends by
the divisor.
(60 ÷ 6) + (24 ÷ 6)
After you have divided each smaller problem add up
the two quotients.
10 + 4 = 14
Therefore, 84 ÷ 6 = 14

16. Rules for solving a simpler division
problem (distributive property)
 The two smaller dividends MUST add up
to the original dividend.
Example: (91 ÷ 7)
(70 + 21) = 91
 The two smaller dividends MUST be
evenly divisible by the divisor.
Example: (70 ÷ 7) + (21 ÷ 7)
10 + 3
 The divisor NEVER changes.

17. Solve by making a simpler
problem
Share & Show pg. 19 #4
Eileen is planting a garden. She has seeds
for 35 tomato plants, 25 sweet corn plants,
and 18 cucumber plants. She plants them
in 6 rows, with the same number in each
row. How many seeds are planted in each
row?

18. Write Math – Journal
How can solving a simpler problem help
you to solve a difficult problem?

19. Chapter 1 Lesson 5
Explore Division Methods

20. Problem Solving pg.24
Use the supply list to solve 14-16
Use partial quotients to solve the problem.
14. Some students are making story maps
out of construction paper. Each student
uses 6 sheets of construction paper, and
no paper is left over. How many students
are making story maps?
Division problem: ___ ÷ ___
___ students are making story maps.

21. Problem Solving pg.24
Use the supply list to solve 14-16
Use partial quotients to solve the problem.
15. Each class that enters the model bridge
competition must submit at least 5 models.
Each model takes exactly 9 straws and 6
paper clips. Does this class have enough
supplies to participate in the competition?
Explain your reasoning.

22. Write Math - Journal
17. Jacob and Gracie used partial quotients to
solve 96 ÷ 8. Jacob used 10 x 8 and 2 x 8 to
solve the problem. Gracie used 5 x 8, and 2 x 8
to solve the problem. Explain why both
methods are correct.

23. Chapter 1 Lesson 6
Estimate Quotients and Use Mental Math
 Susan is biking the 42-mile Suncoast Trail from
north of Brooksville to Land O’Lakes. She plans to
stop every 5 miles along the trail to drink water.
About how many times does Susan plan to stop for
water on the trail?
 What phrase is used to indicate you are looking for an estimate and not
an exact answer?
 Estimate 42 ÷ 5
 Use multiplication: 5 x __ = 40 5 x __ = 45
 Use division: 40 ÷ 5 = __ 45 ÷ 5 = __
Since ___ is closest to 42, a good estimate for 42 ÷ 5 is about ___.
So, Susan will stop for water about ___ times.

24. Mental Math – Use the Distributive Property can help you rewrite a
dividend so it’s easier to divide.
 Example 1: Divide 76 ÷ 4
 Step 1 – Break apart the dividend into addends whose sums
equal the dividend. These addends should be easily divisible by
the divisor.
○ (40 + 36) ÷ 4
 Step 2 – Use mental math to divide the addends by 4.
○ (40 ÷ 4) + ( 36 ÷ 4)
10 + 9
Therefore, 76 ÷ 4 = 19
 Example 2: Divide 51 ÷ 3
You can use a close dividend and compensate by adding or
subtracting the difference.
Think: 51 is close to 60, and you can mentally divide by 3.
Think: 51 is 9 less than 60. Compensate by subtracting 9 from 60.
(60 – 9) ÷ 3
(60 ÷ 3) - (9 ÷ 3)
20 - 3
Therefore, 51 ÷ 3 = 17

25. Problem Solving pg. 30
18. Mrs. Johnson makes 78 cupcakes for the
fifth-grade classes. She will put the 6
cupcakes in each of several boxes. How
many boxes will Mrs. Johnson need for all
of the cupcakes?
Write a division problem that can be used
to solve the problem.
Solve the problem and explain your
reasoning.

26. Write Math – Journal
How can basic facts and the Distributive
Property help you estimate a quotient or
calculate the quotient mentally?

27. DMSB – Divide Multiply Subtract Bring down
Chapter 1 Lesson 7
Practice Division

28. Checking division – use the inverse operation of division
(multiplication) to check your answer to a division problem .
 To check your answer to a division problem,
multiply the quotient by the divisor. The product
should be the dividend.
 Divide: 84 ÷ 7 Divide: 79 ÷ 6
 Check: Check:

29. Unlock the Problem pg. 34
30. The owner of a palm-tree farm has 23
silver date palms and 42 pygmy date
palms. He plans to plant all the palms in 5
rows that have equal numbers of trees.
How many palms will be in each row?
The palm-tree farm has a total of ___
palms. There are ___ rows of palms.
There are ___ palms in each of the rows.

30. Write Math – Journal
How can you use place value to solve a
division problem?

31. Equation – a number sentence that uses the equal sign to show the two
amounts are equal.
Variable – a letter or symbol that stands for an unknown number or numbers
Chapter 1 Lesson 8
Solve Equations

32. Try This! Pg. 36

33. Problem Solving pg. 37
25. David has 36 apples. He will give an
equal amount of them to each of 6
friends. How many apples will David
give to each friend? Use the equation 36
÷ a = 6 to find a, the number of apples
each friend will get.
Each friend will receive ___ apples.

34. Problem Solving pg. 37
26. Debbie will make 4 equal payments for
a new game. The game costs $36.
How much will each payment be? Use
the equation 36 ÷ p = 4 to find p, the
amount of each payment.

35. Problem Solving pg. 38

36. Write Math - Journal
How can you use mental math to solve a
division problem?

37. Chapter 1 Review