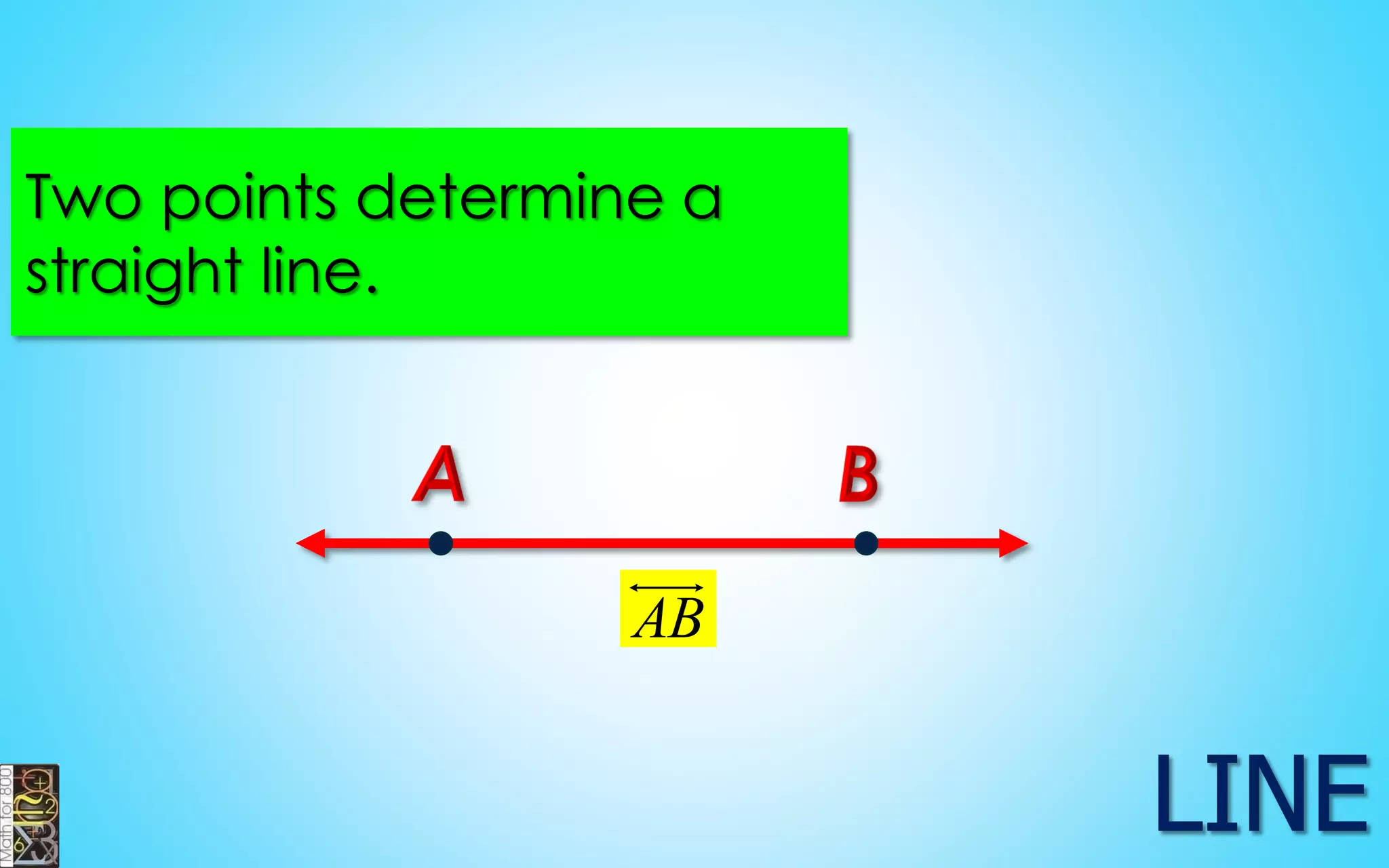
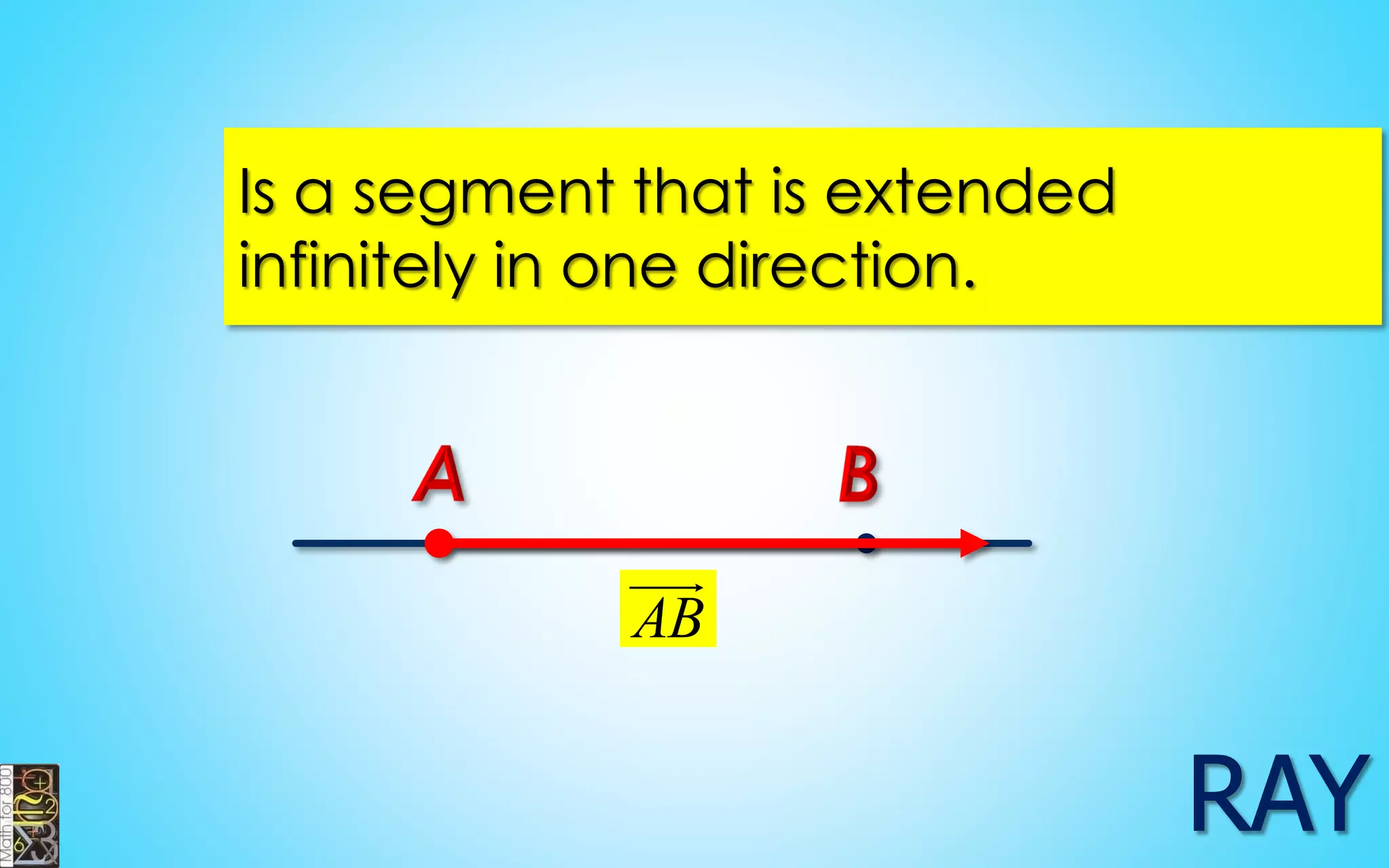
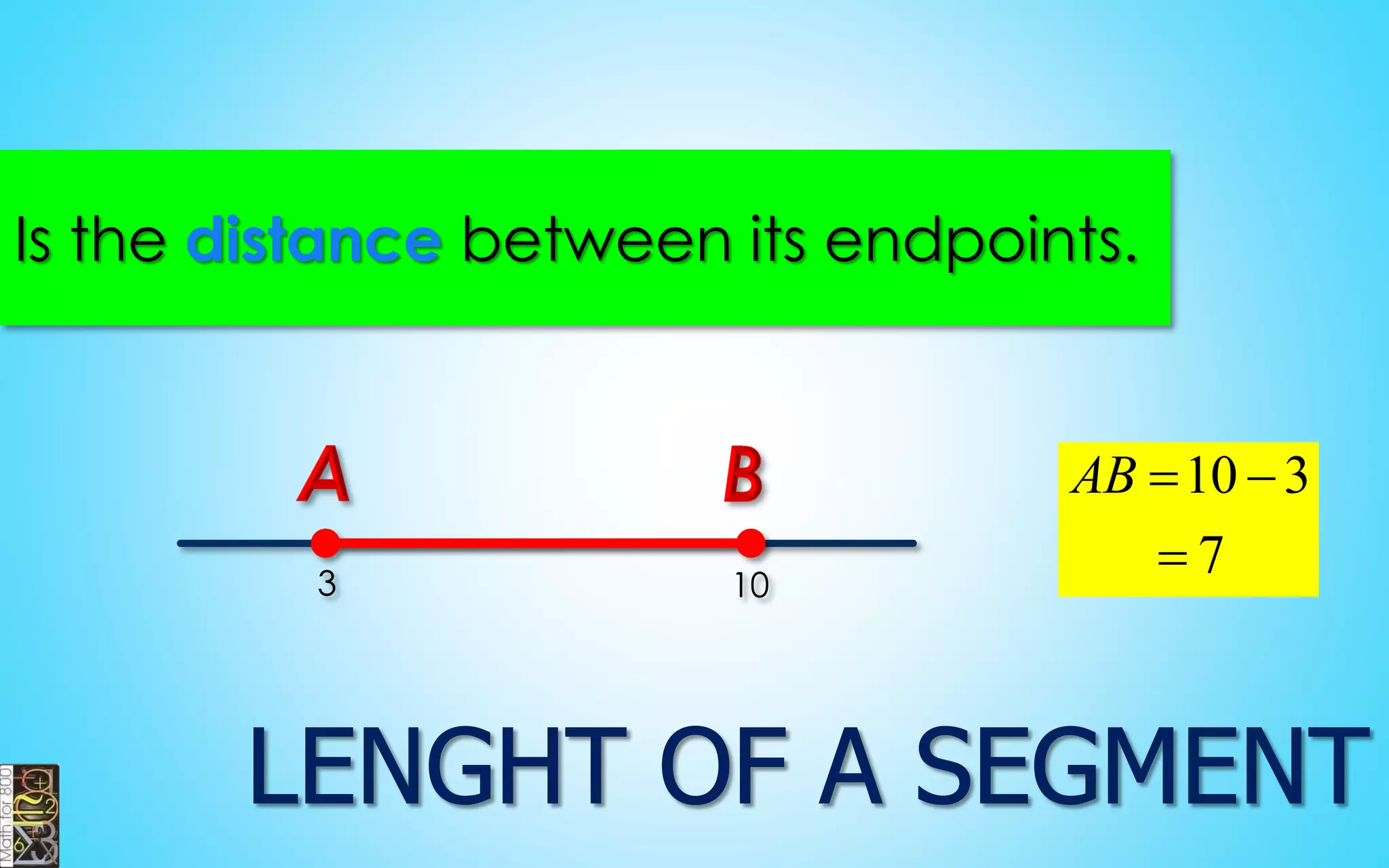
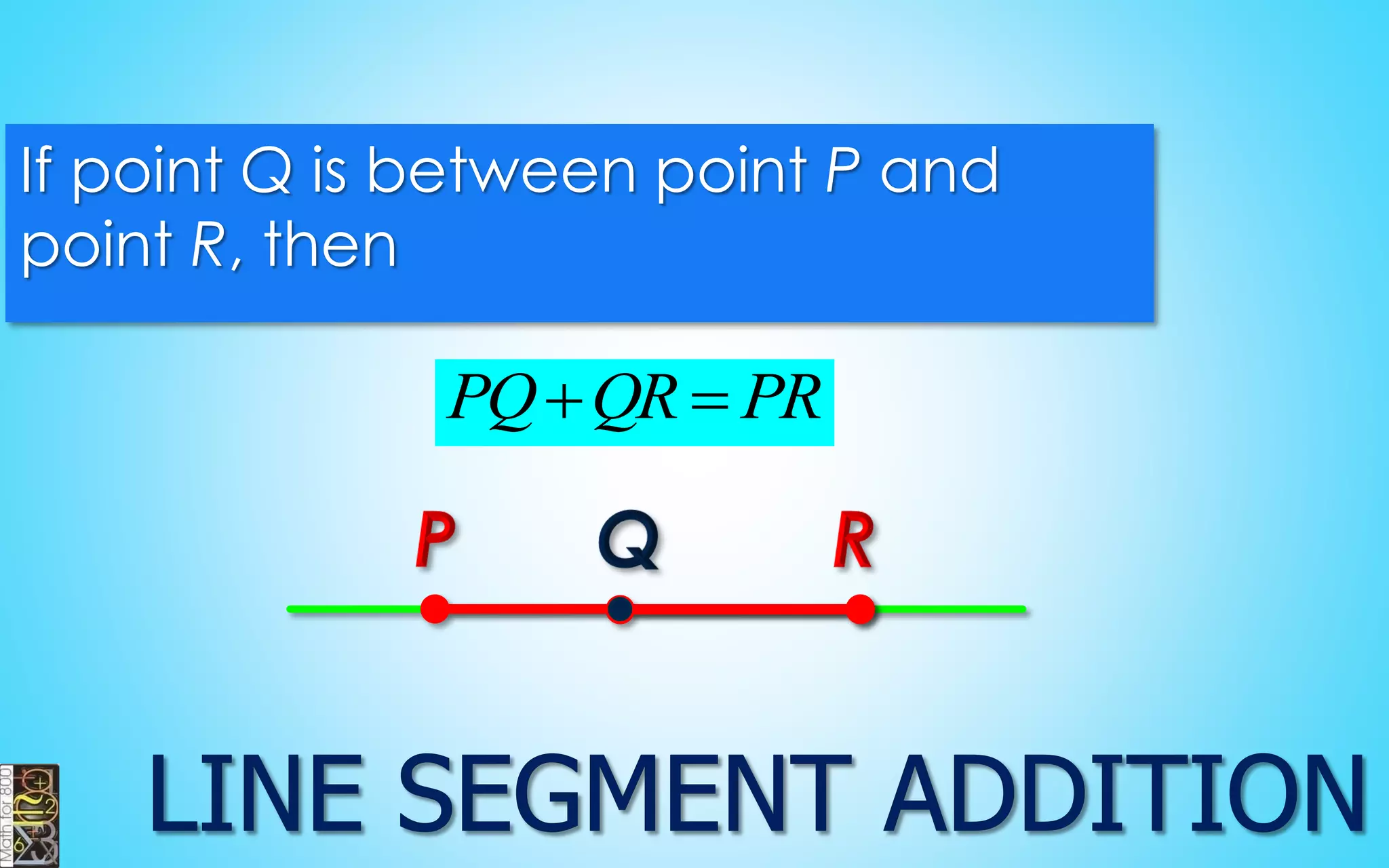
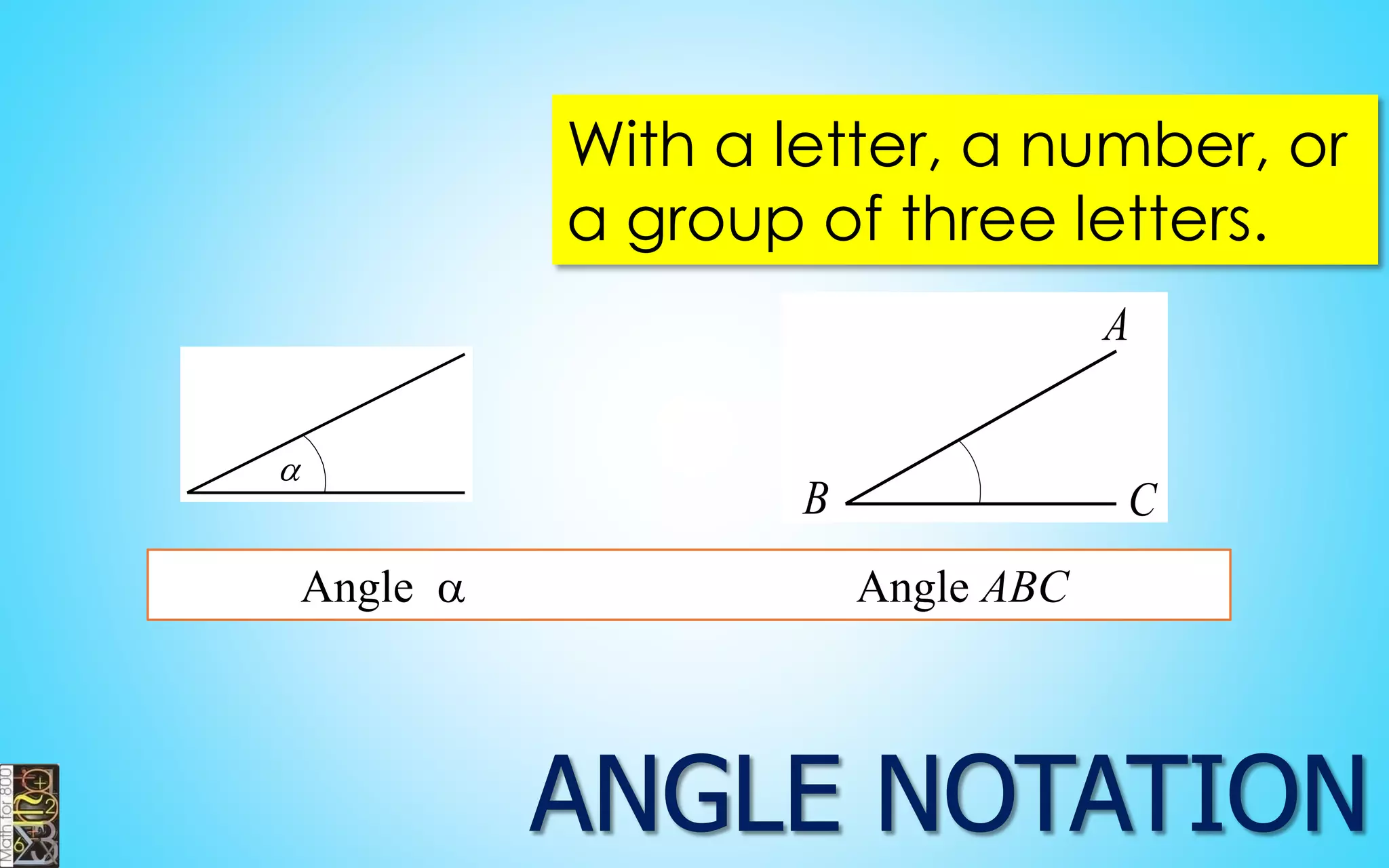
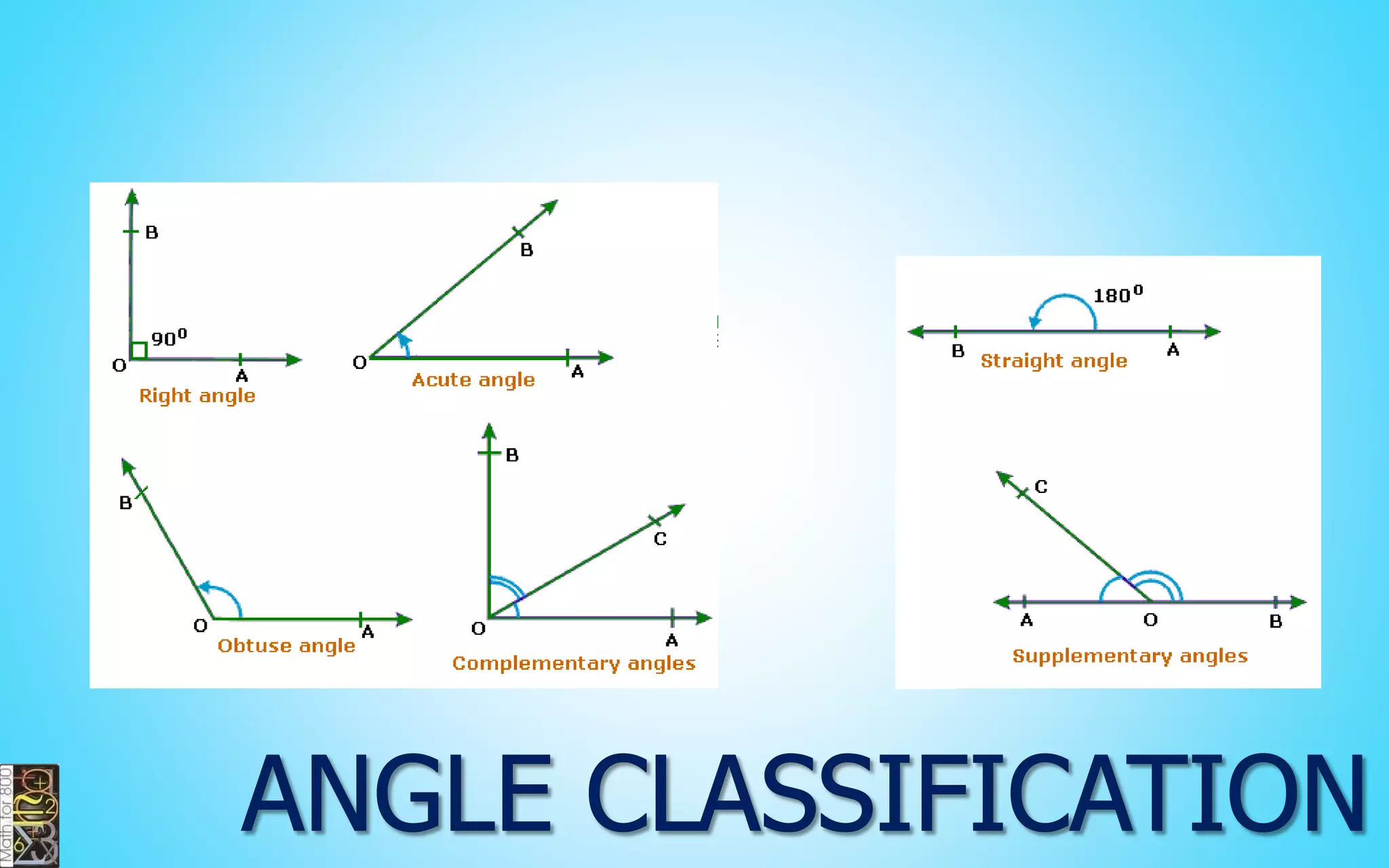
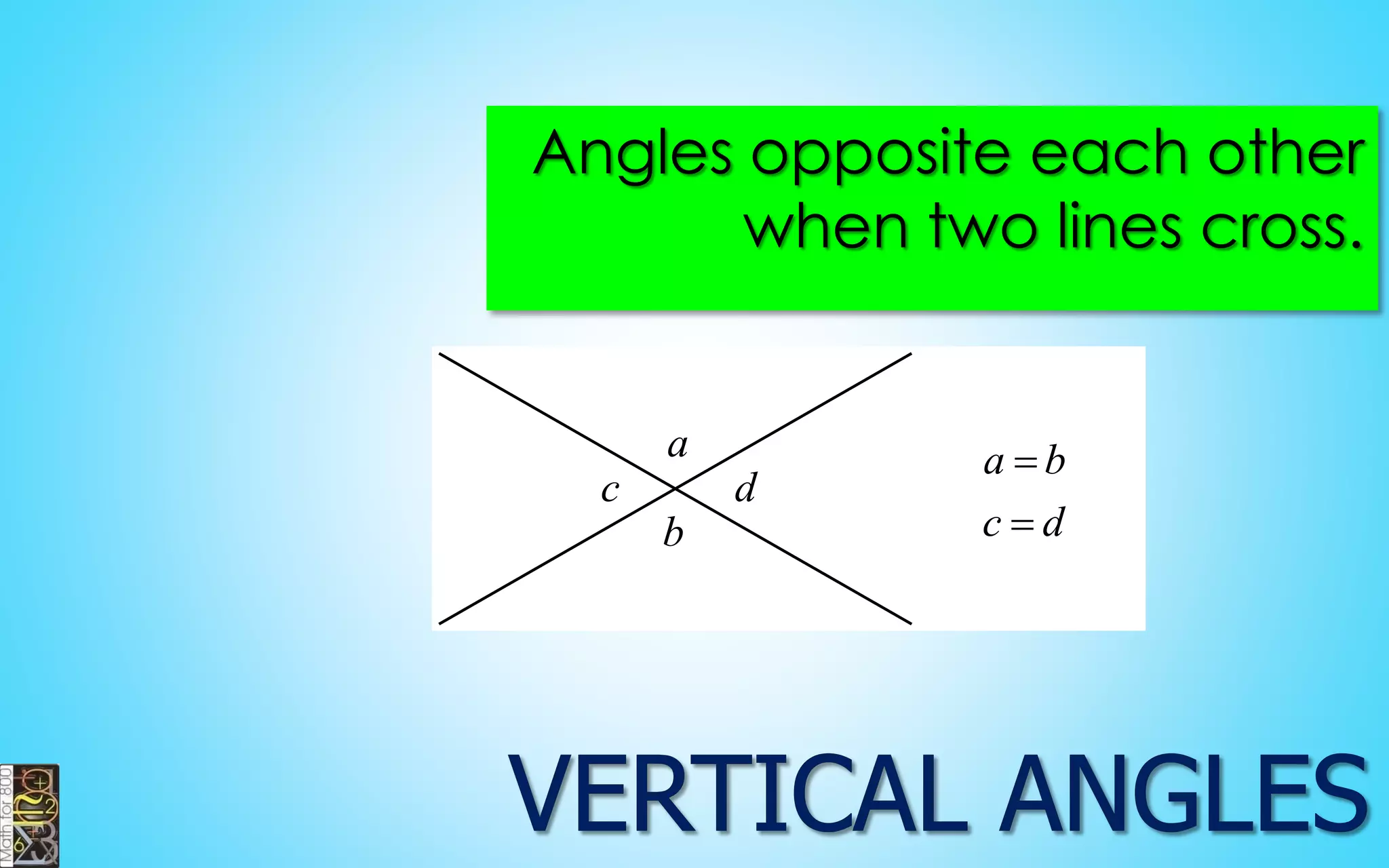
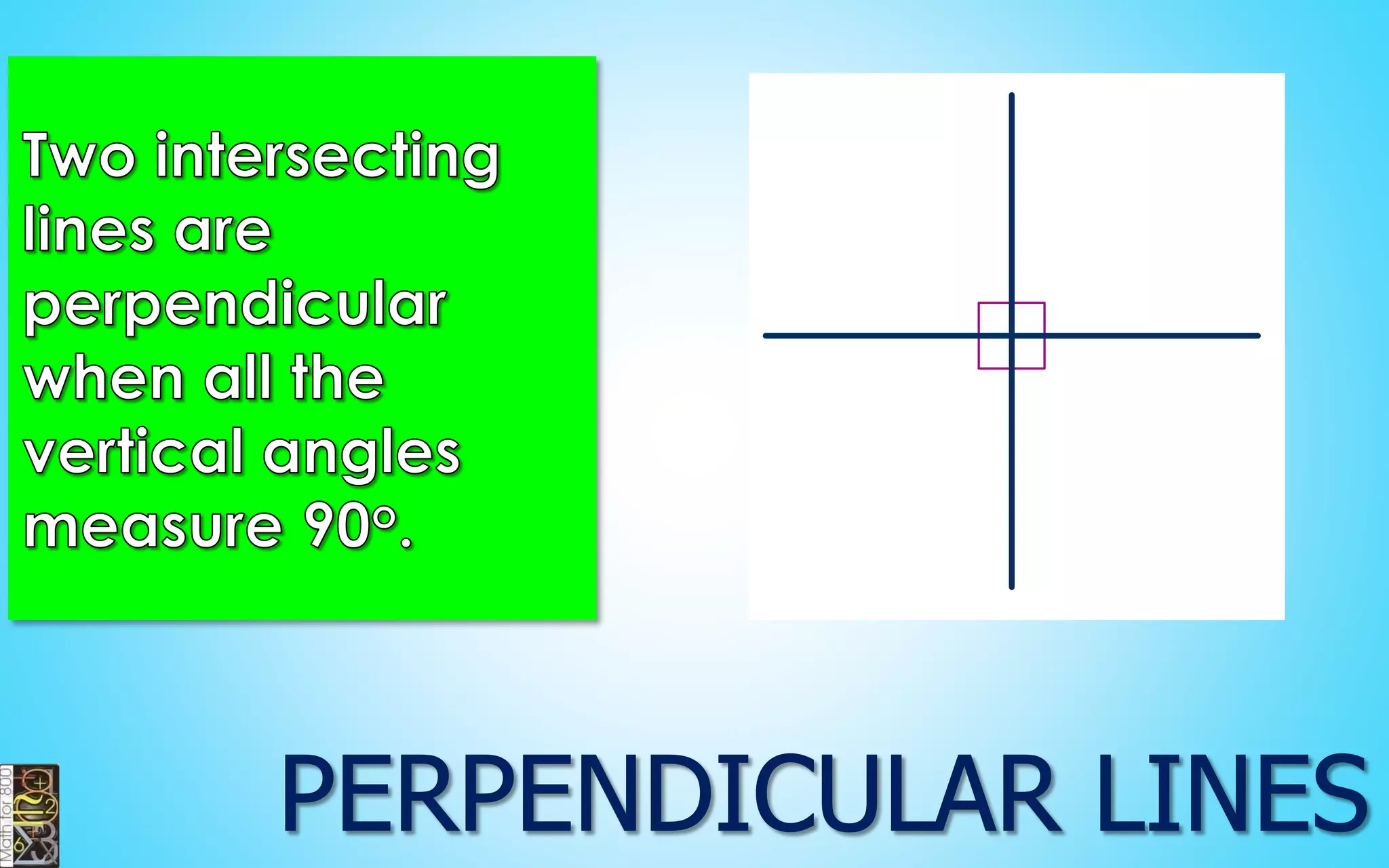
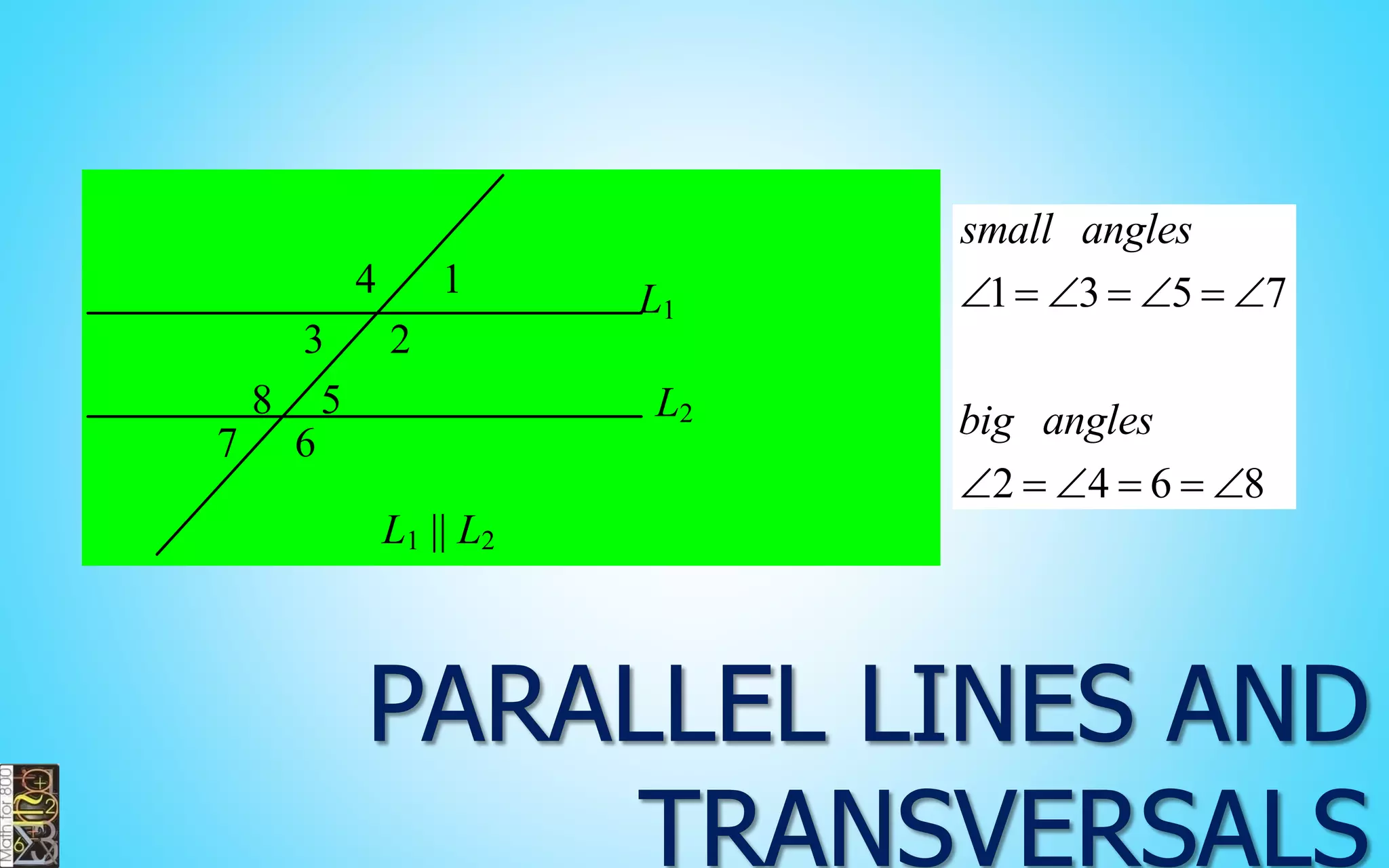
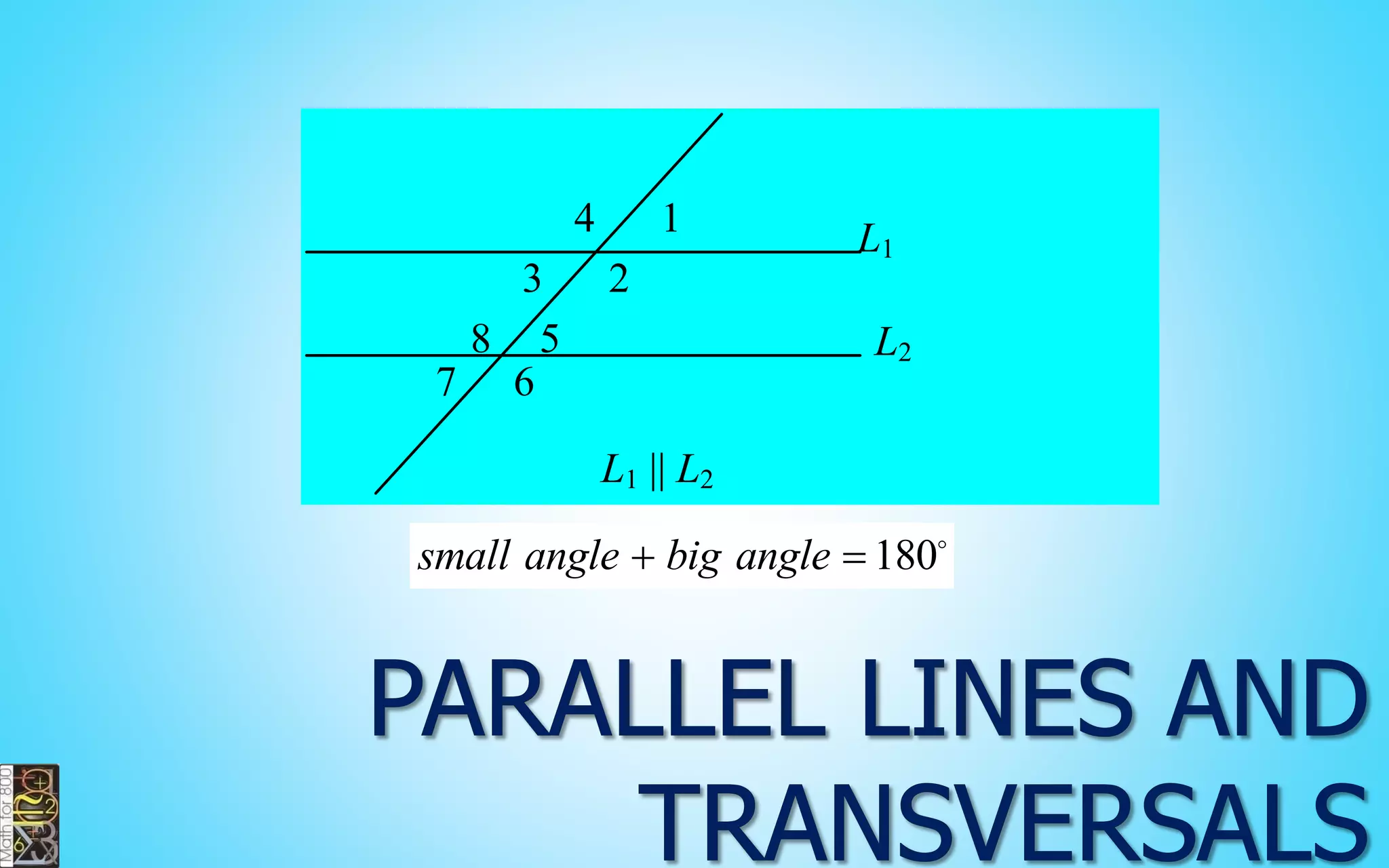
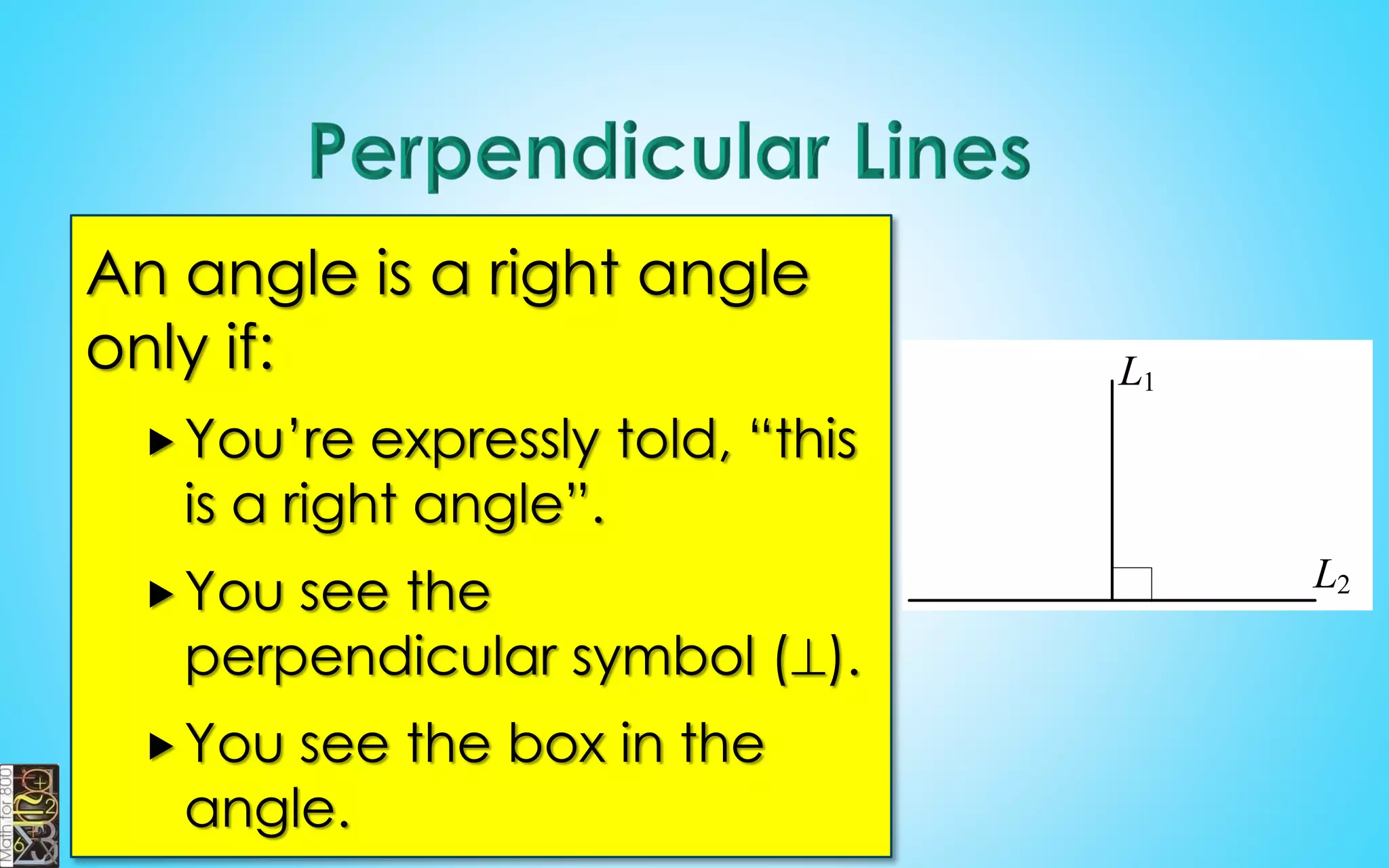
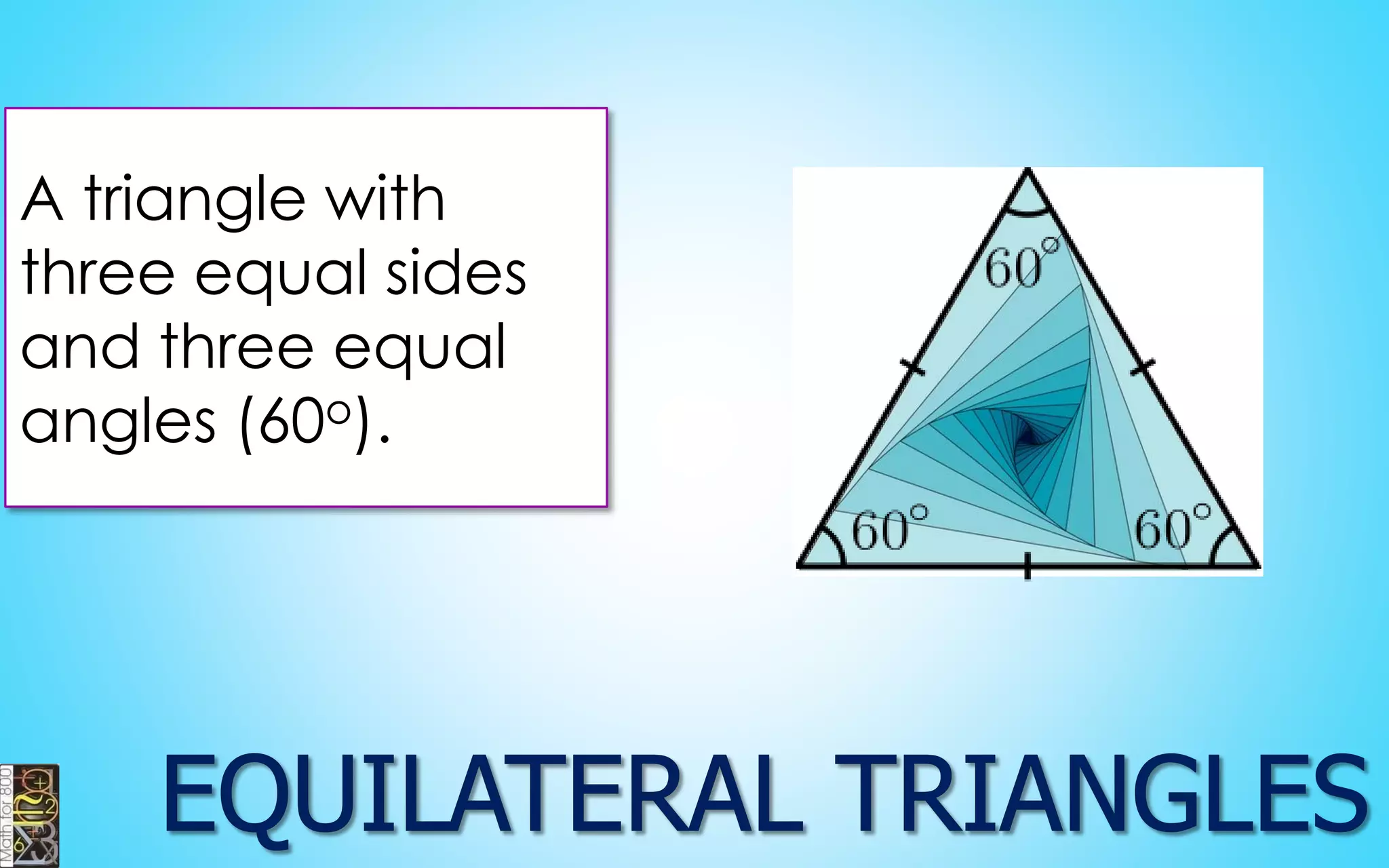
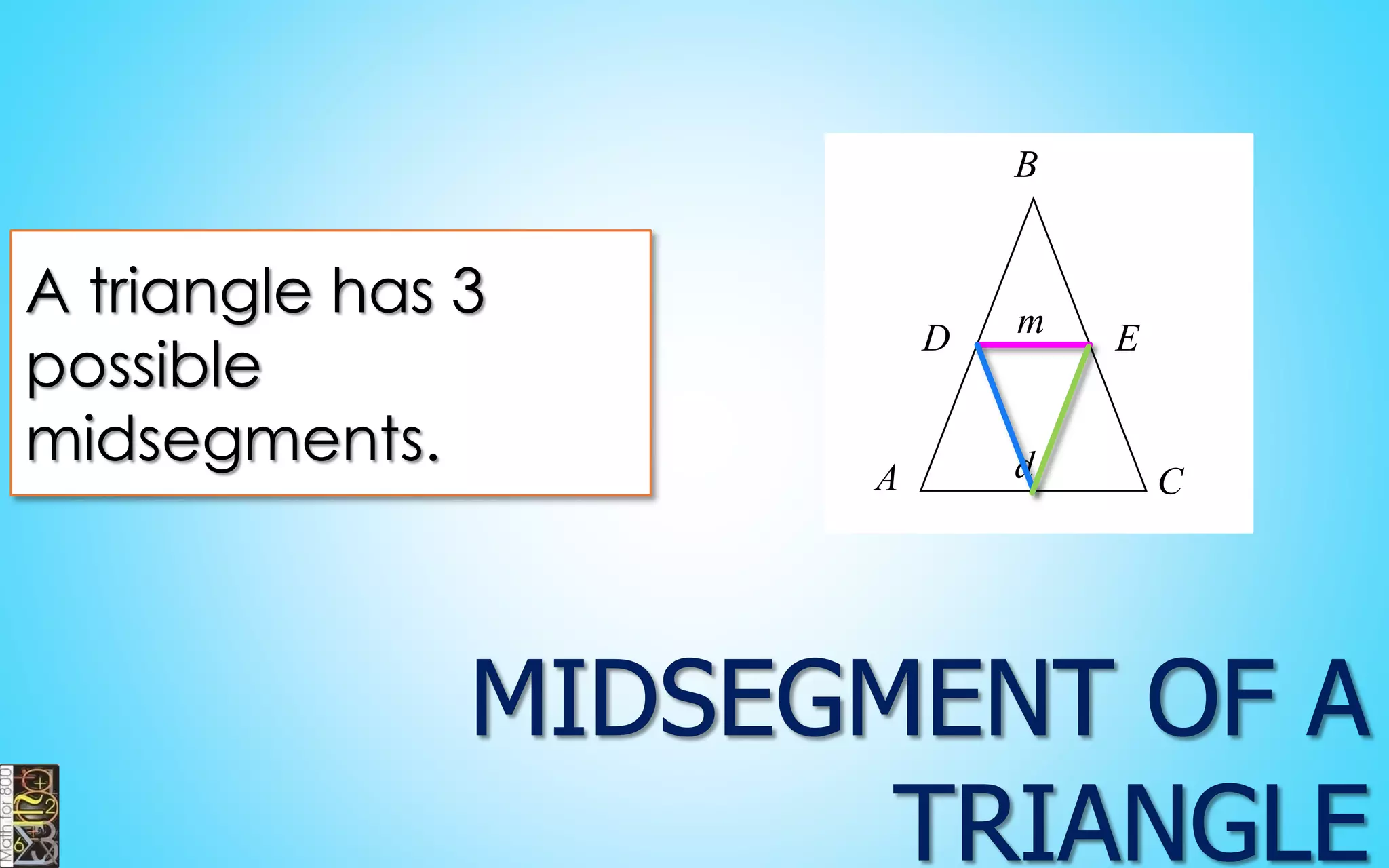
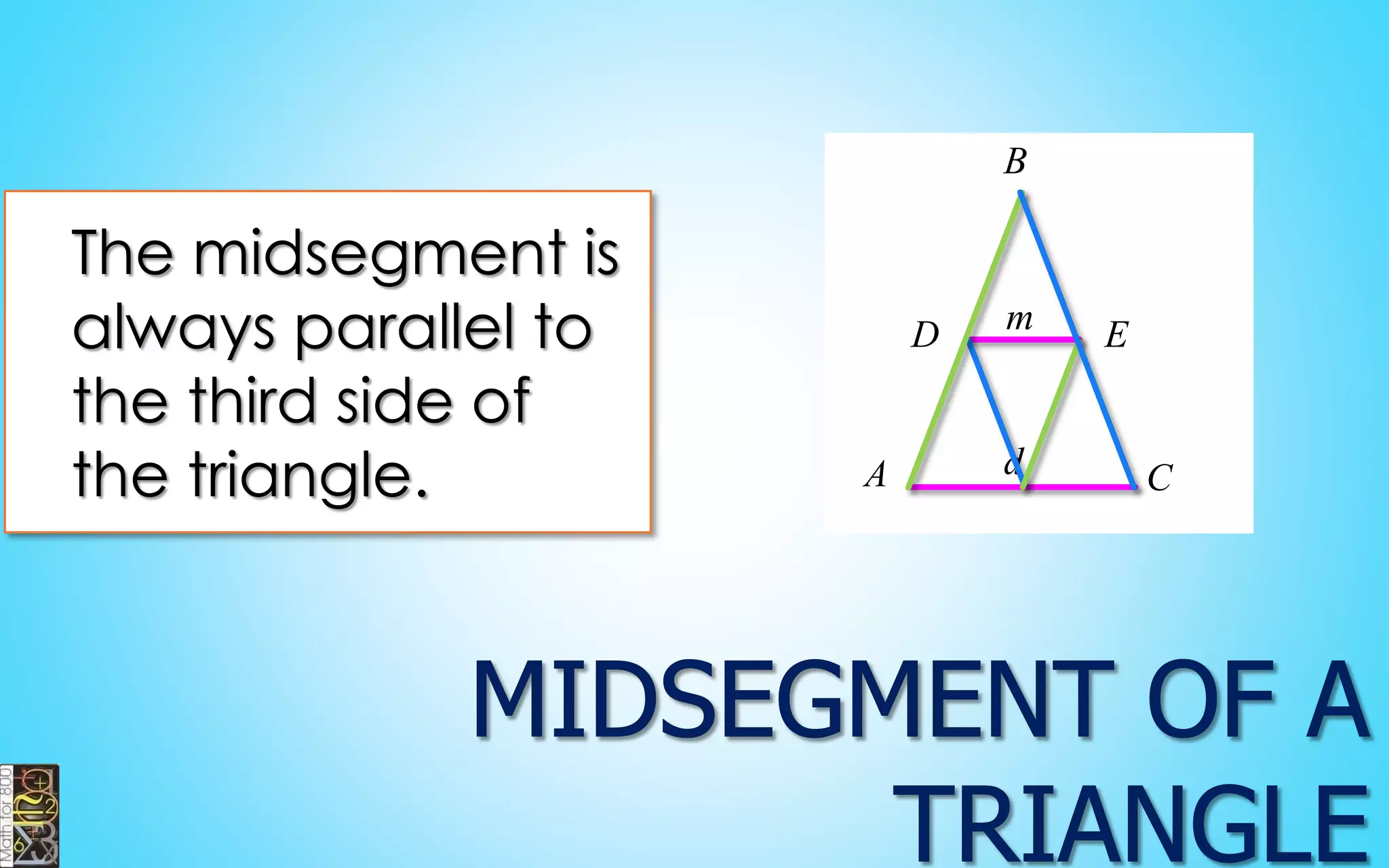
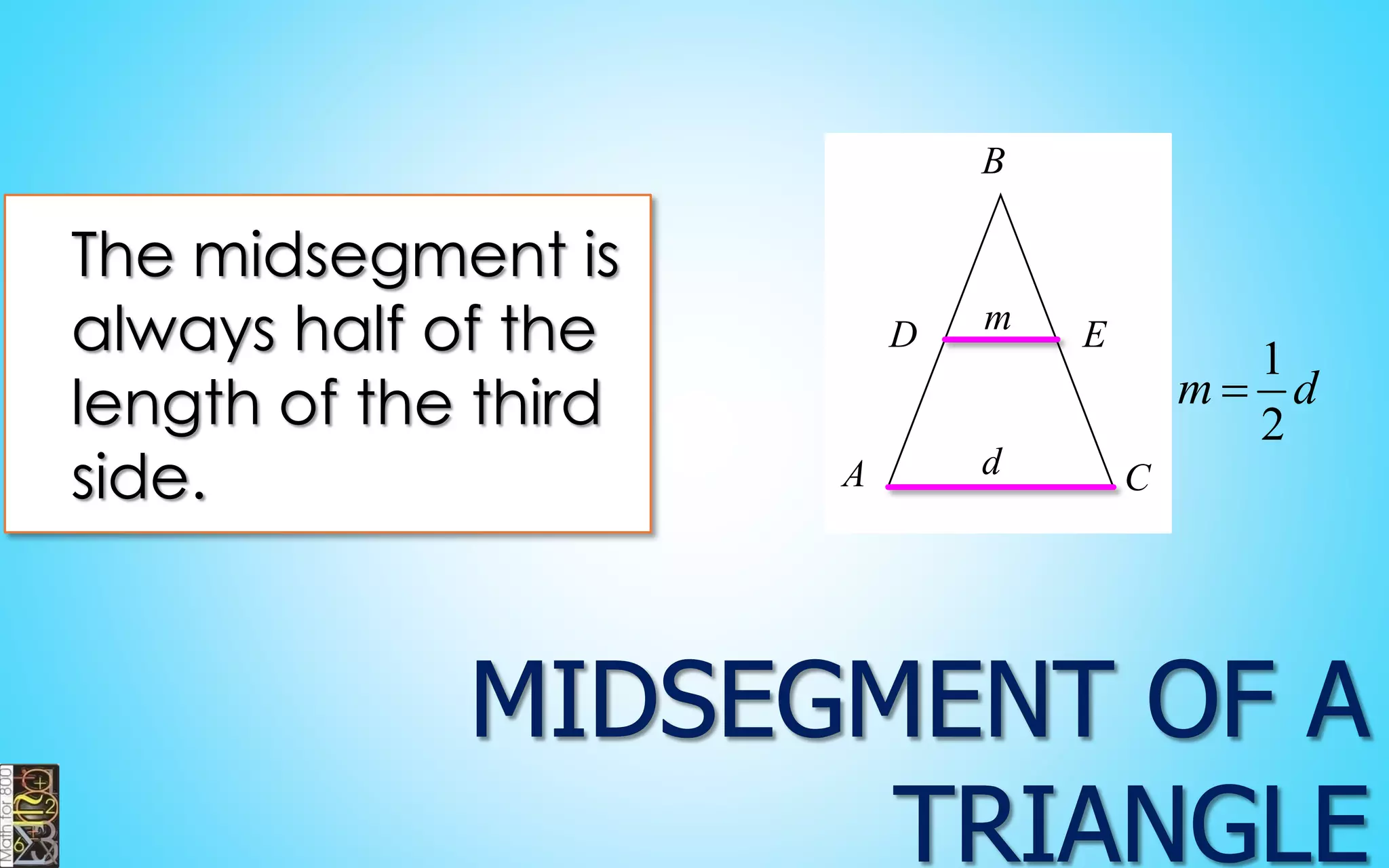
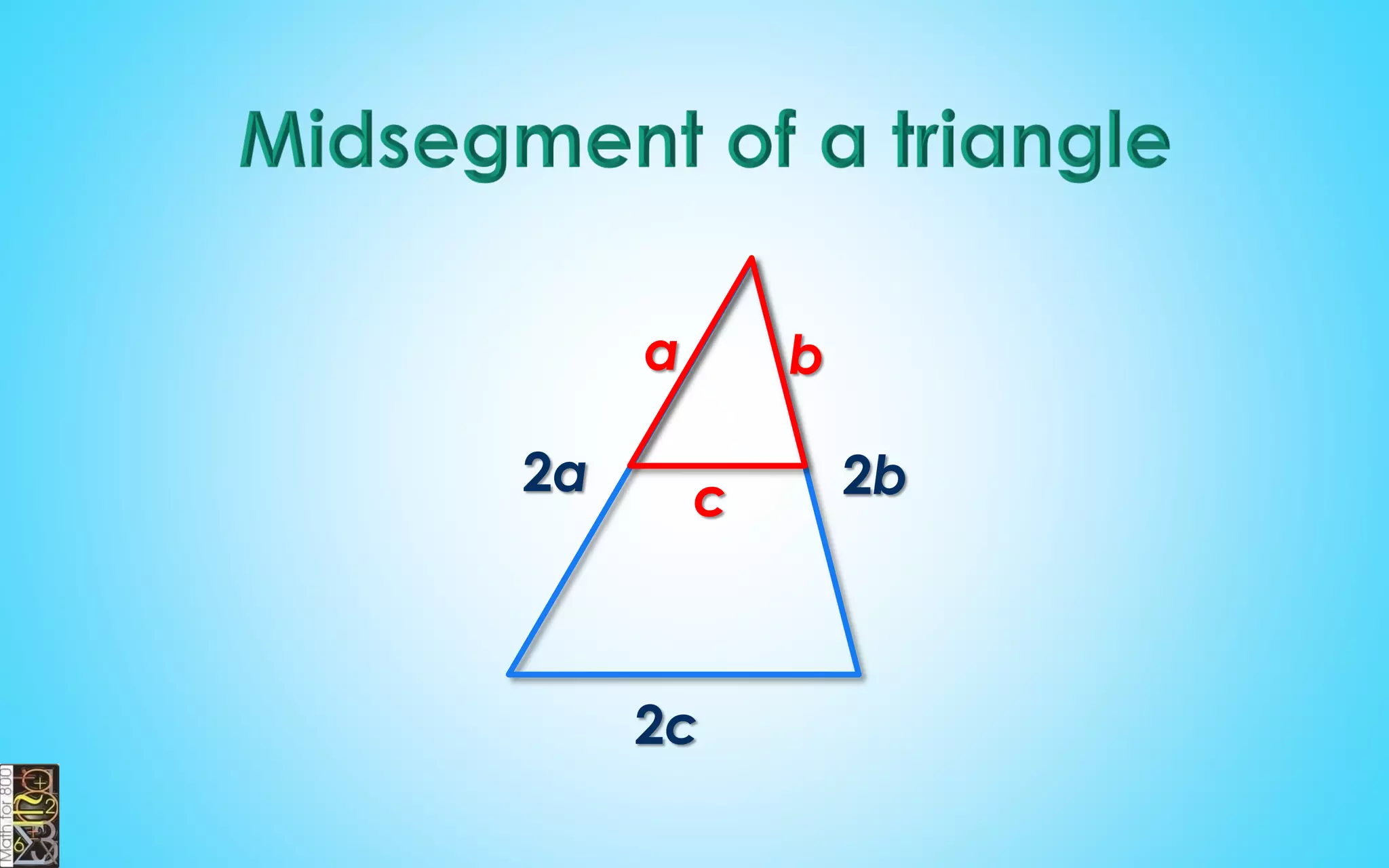
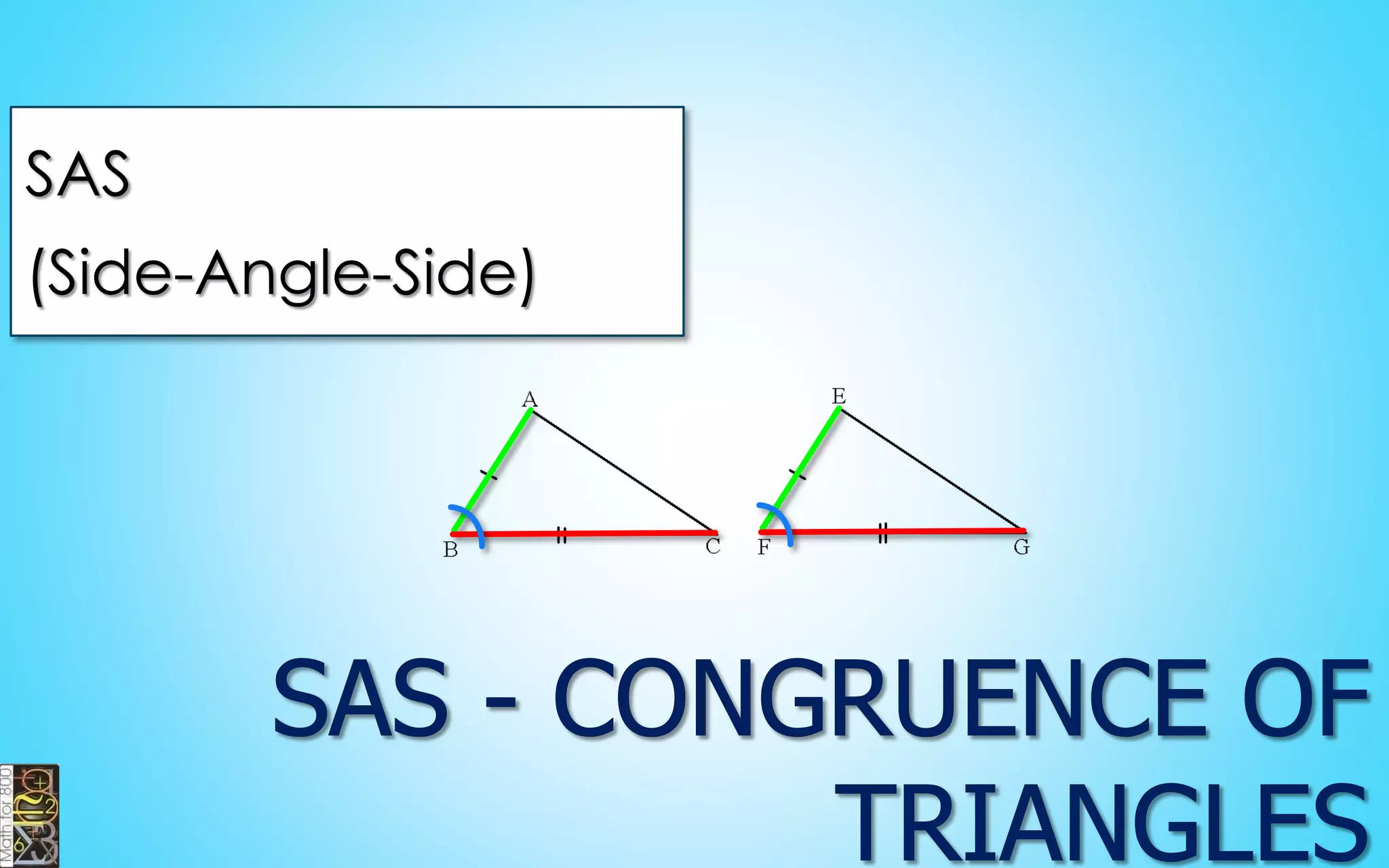
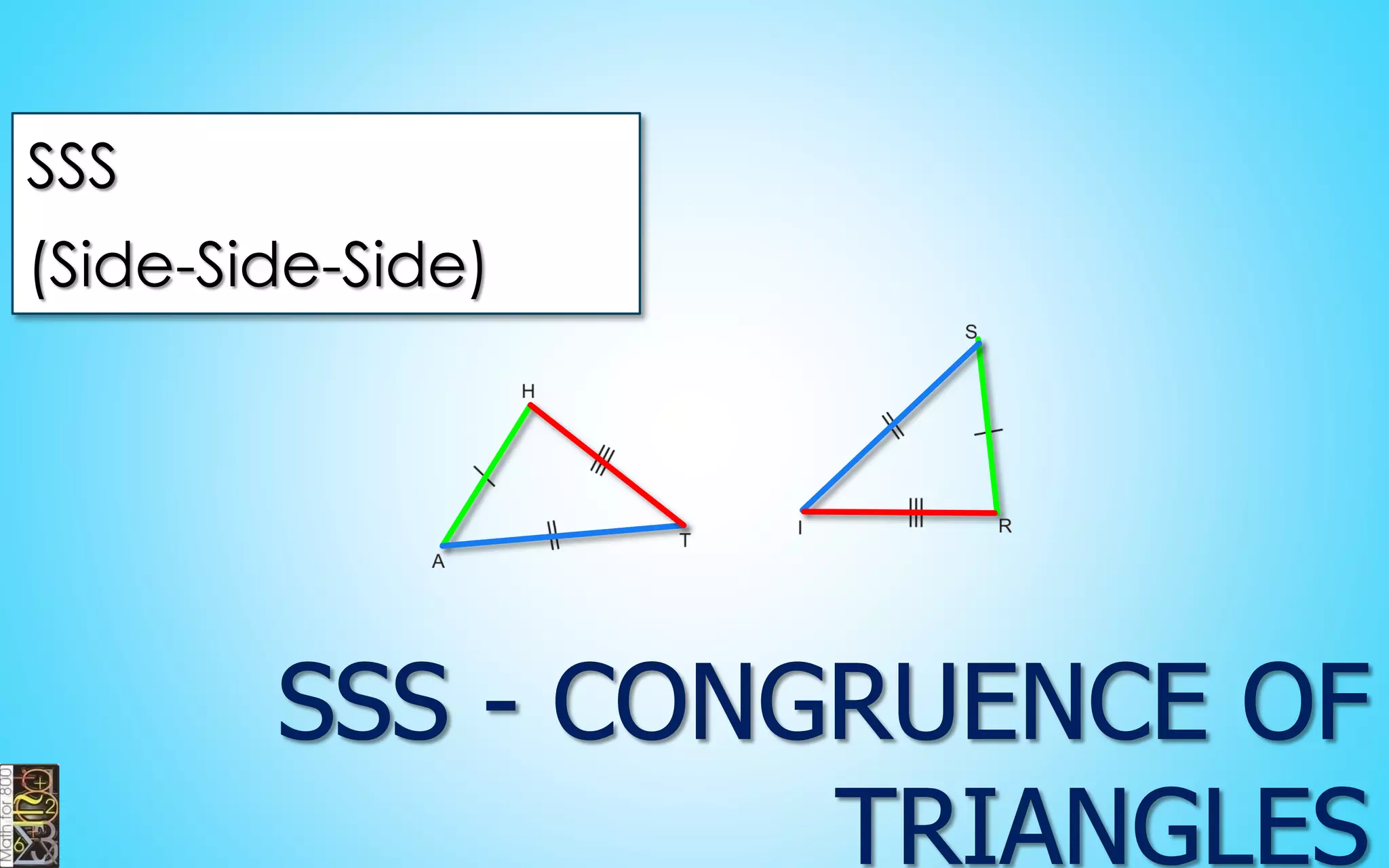
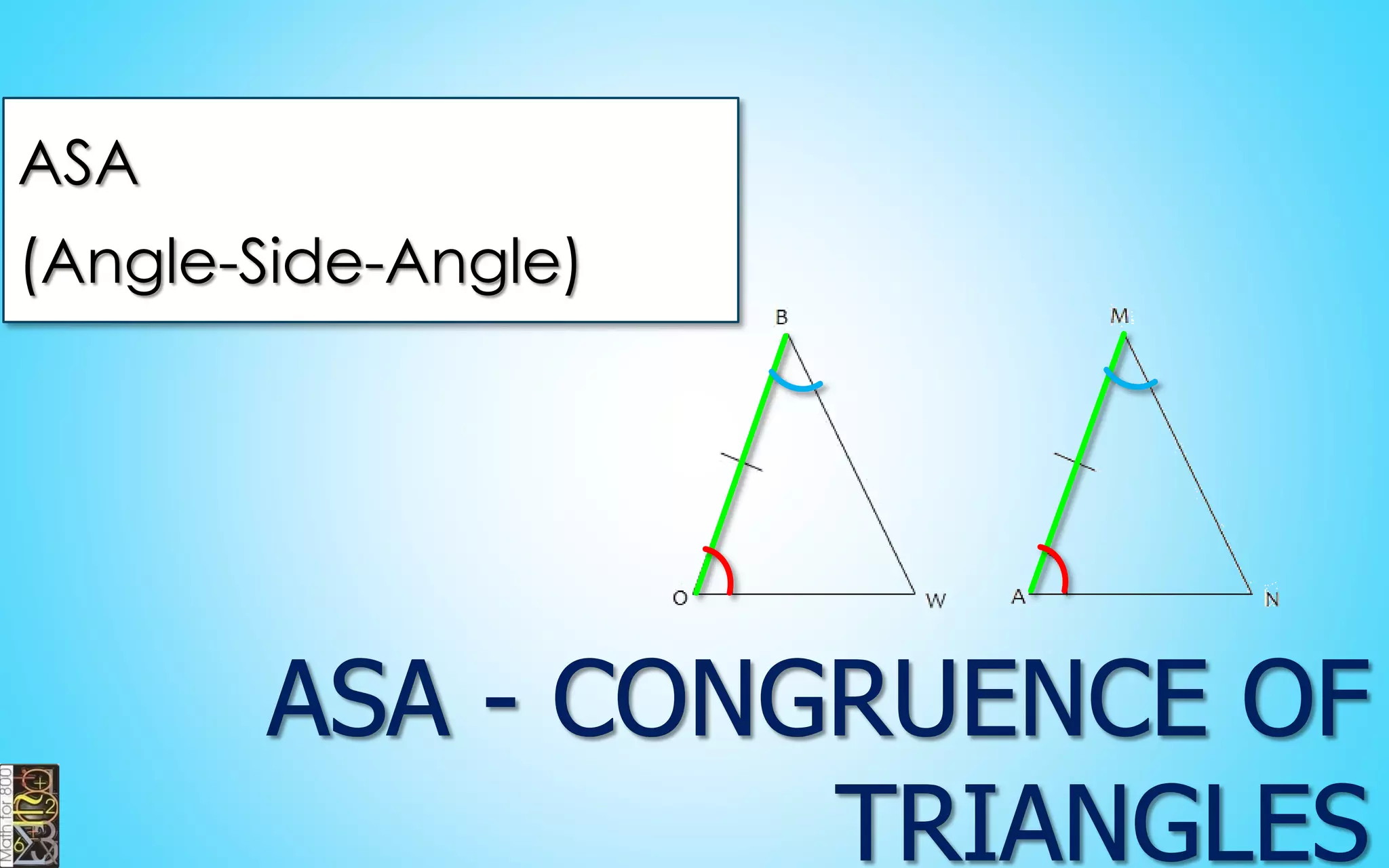
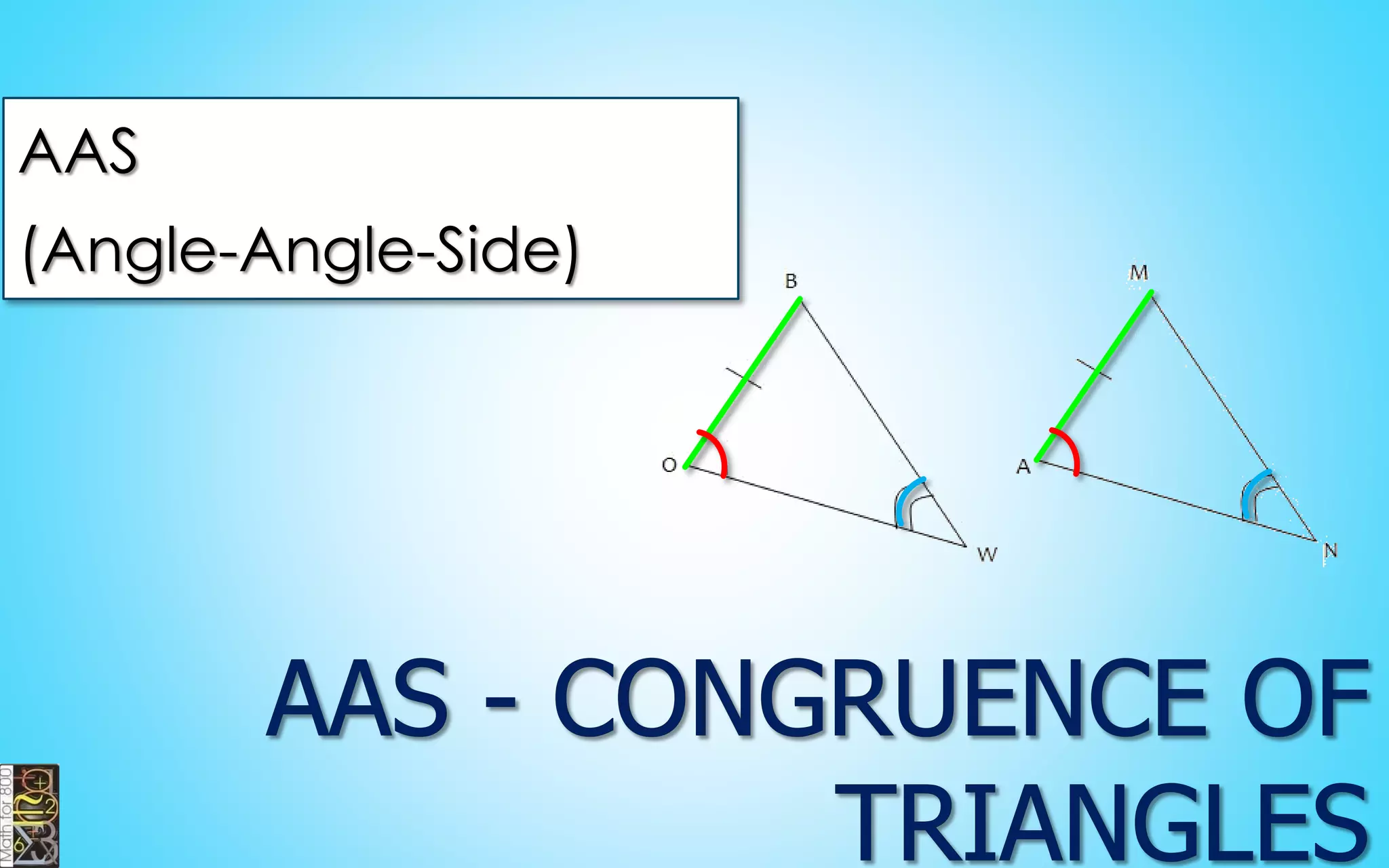
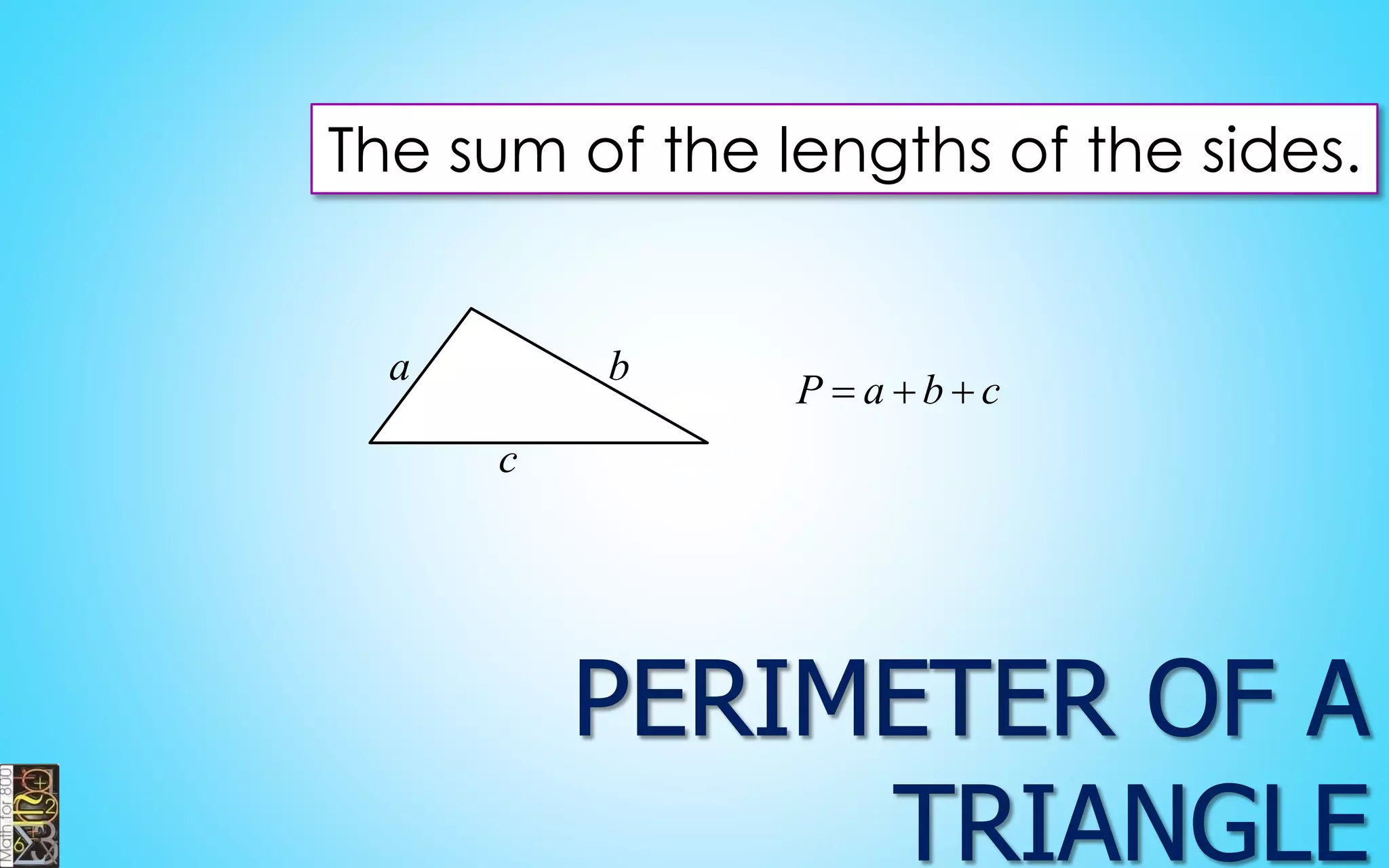
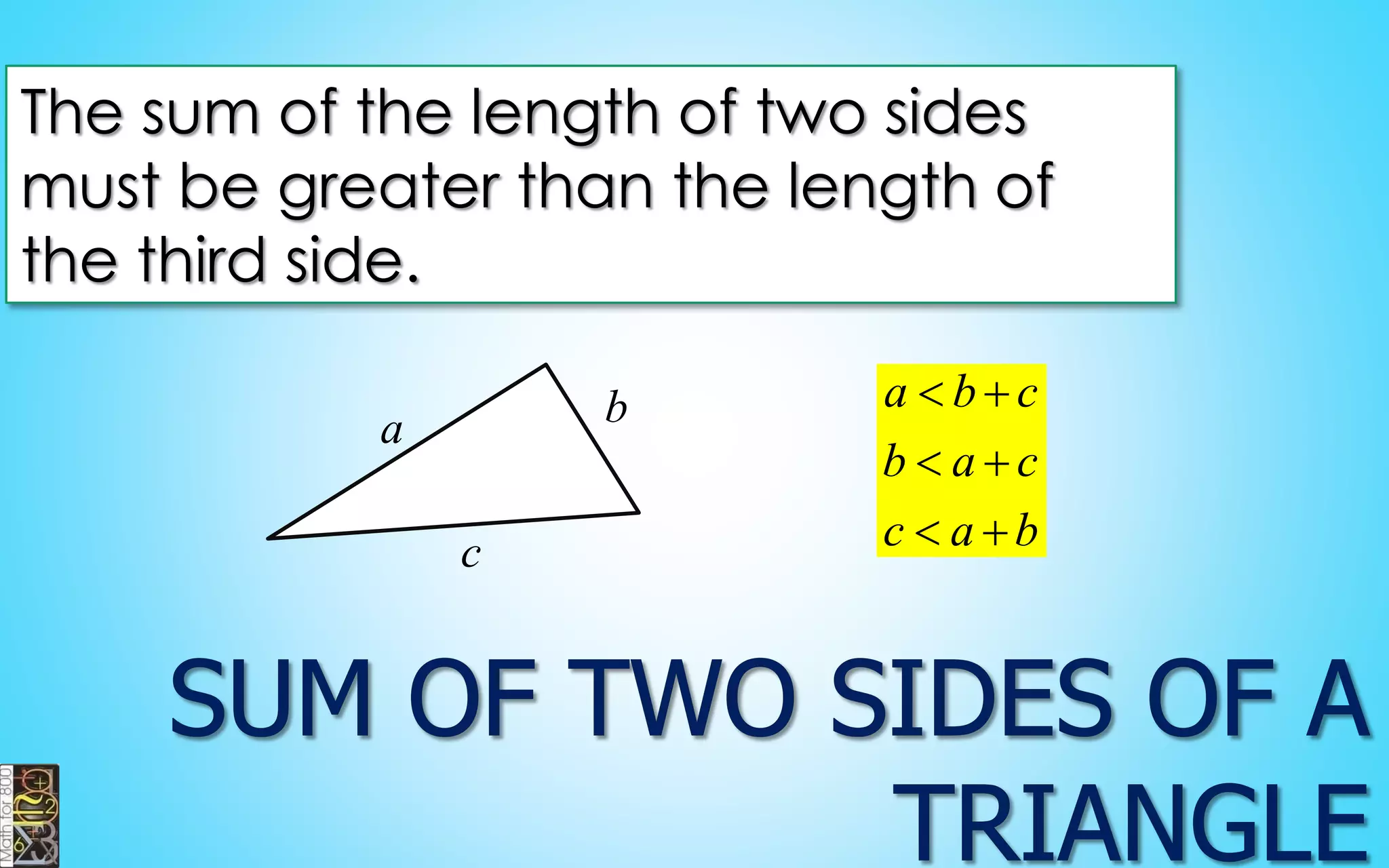
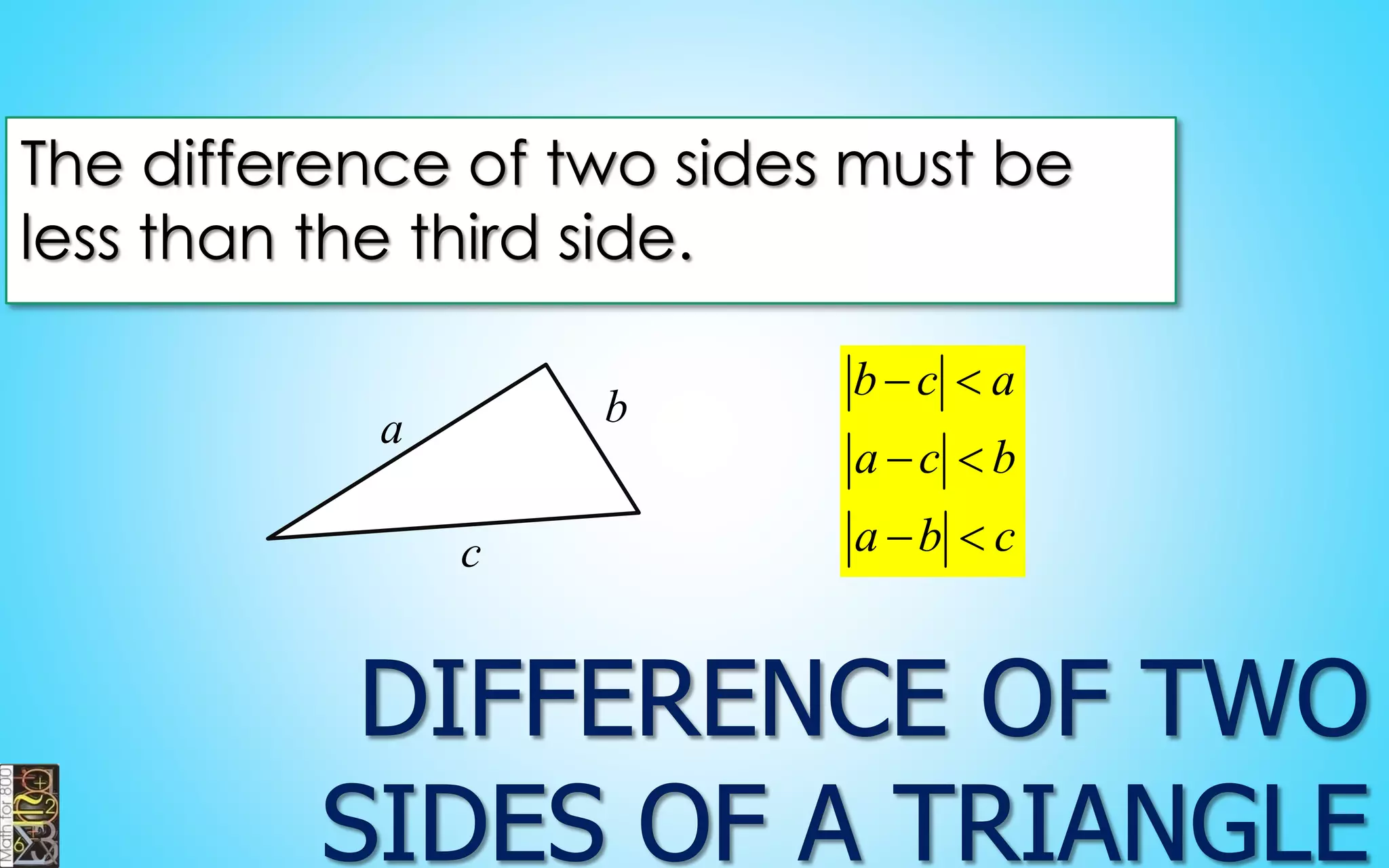
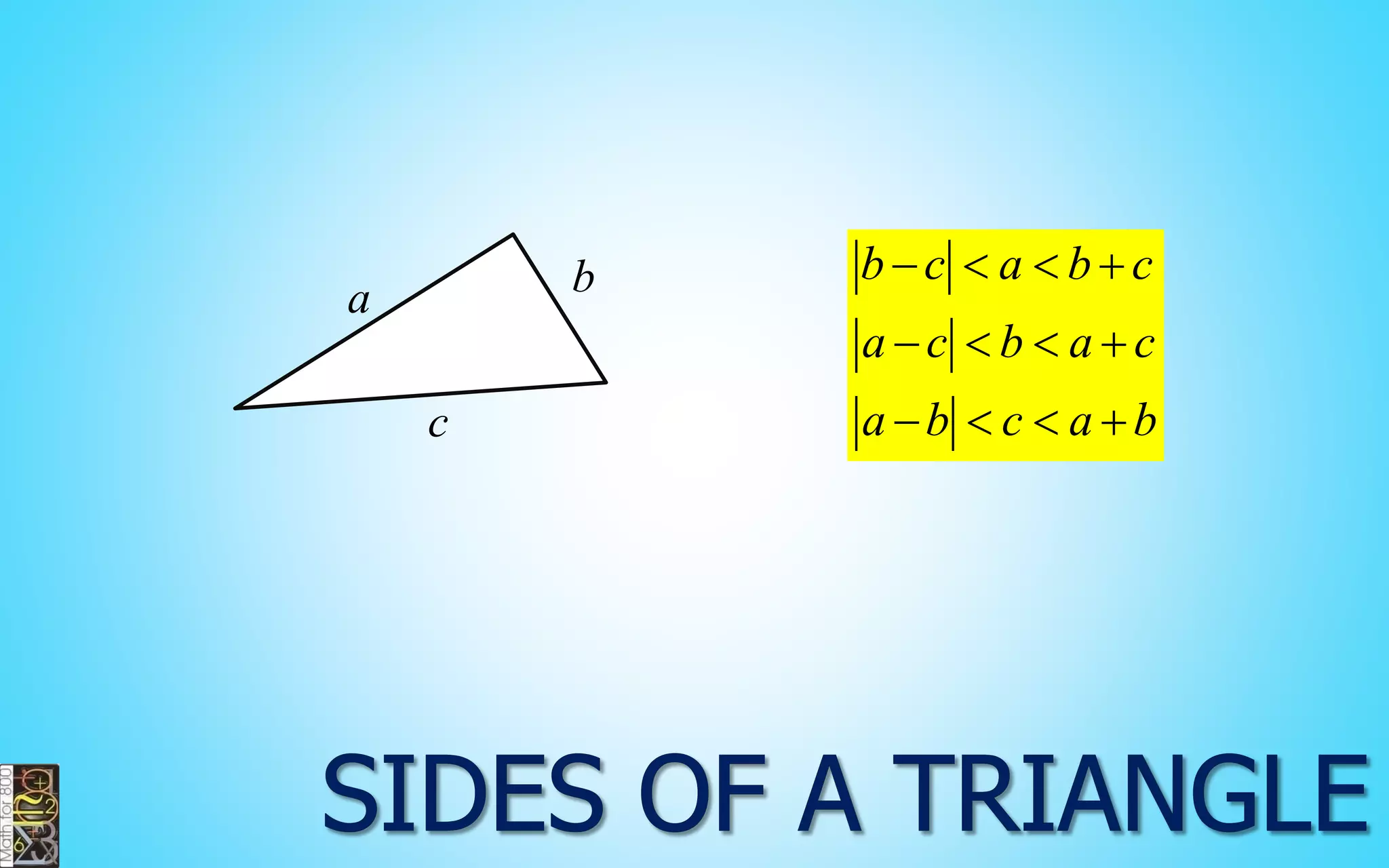
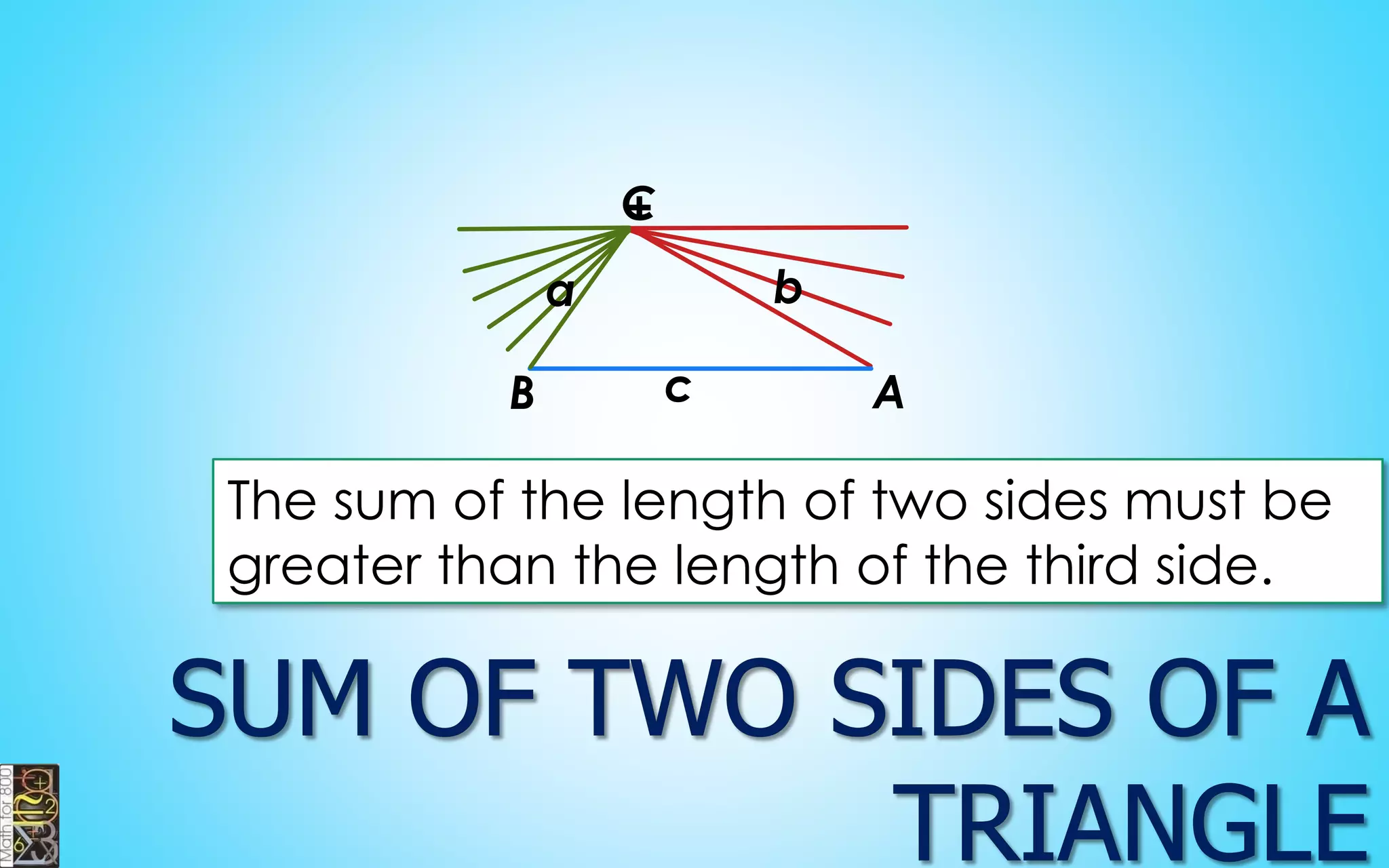
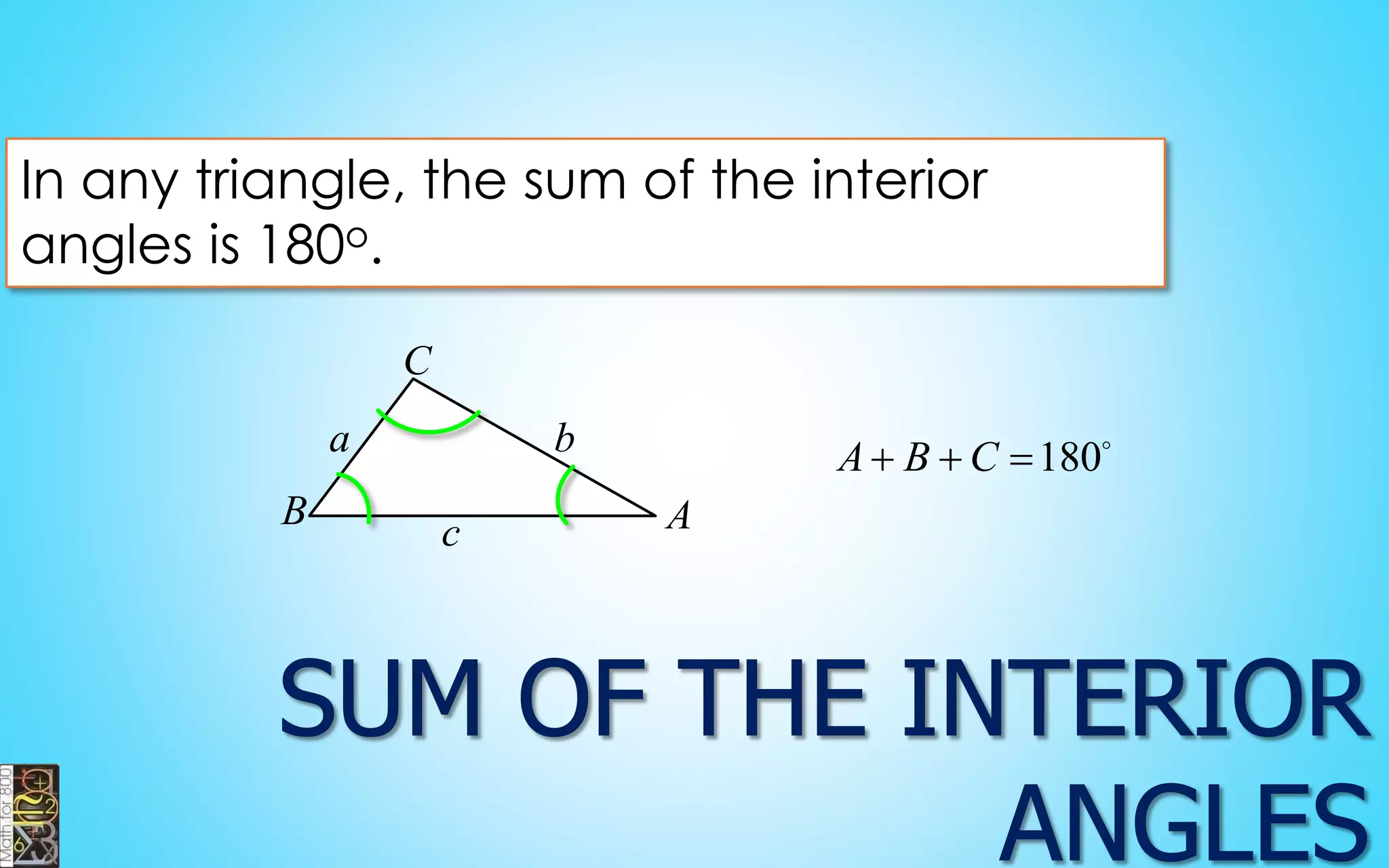
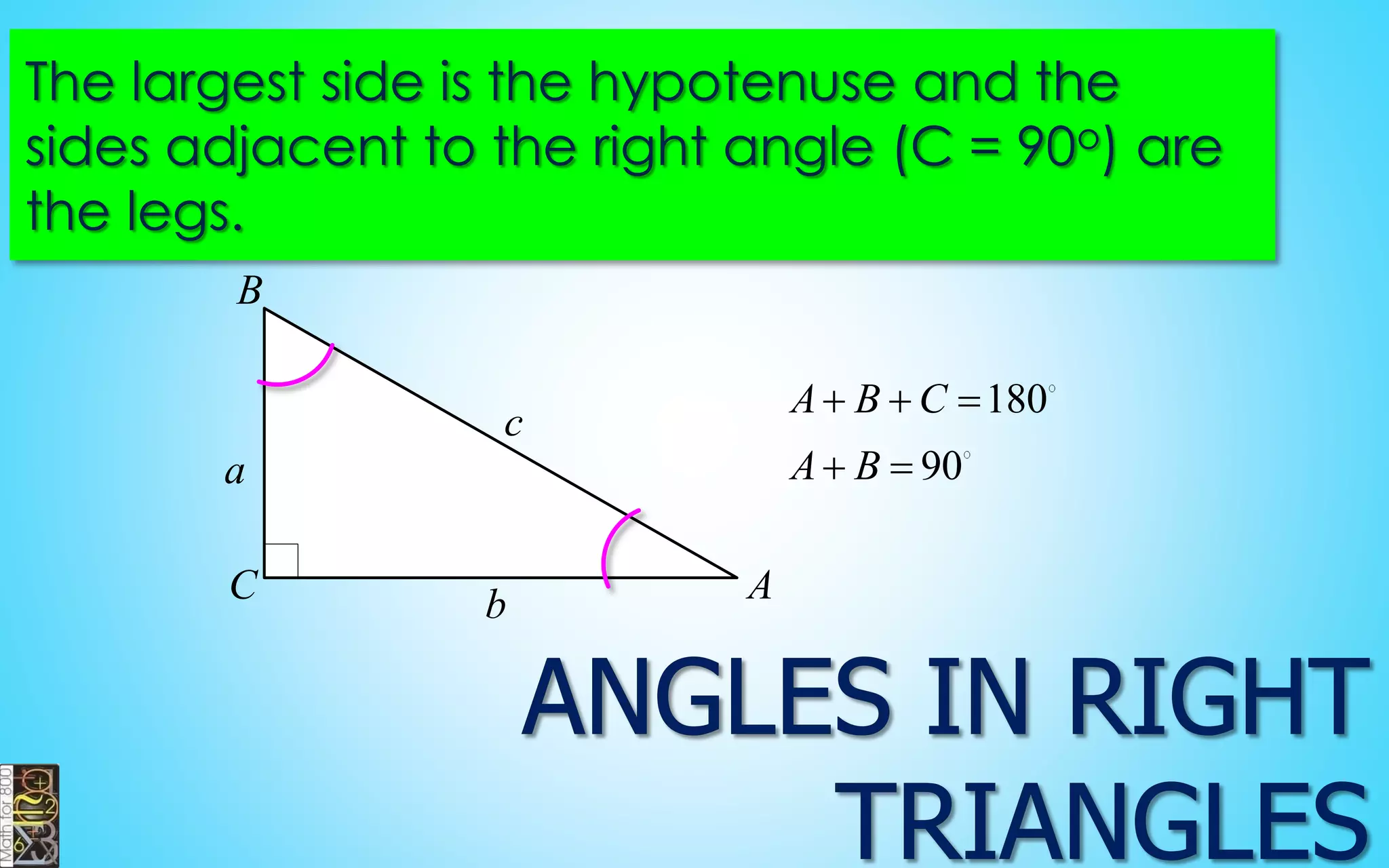
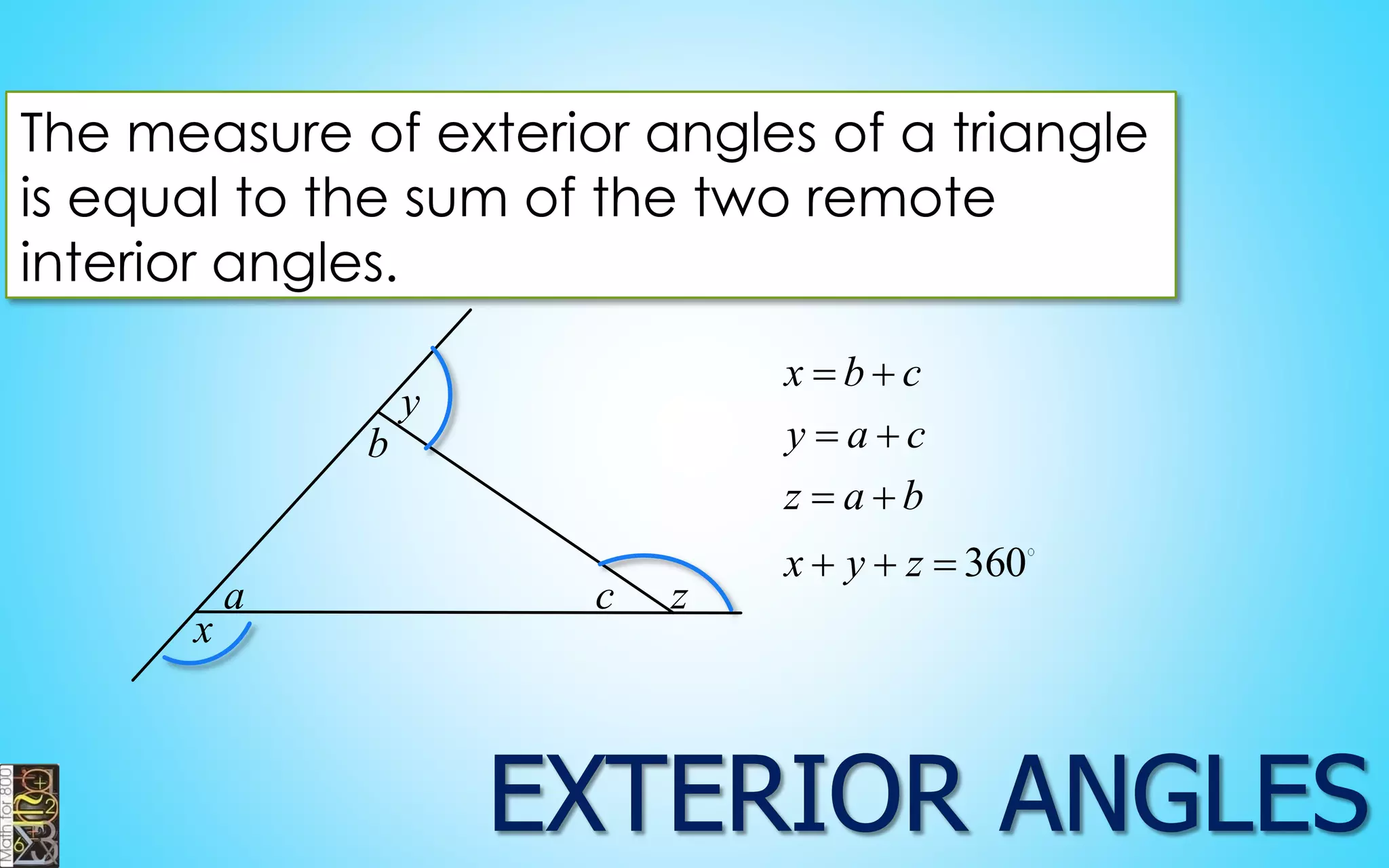
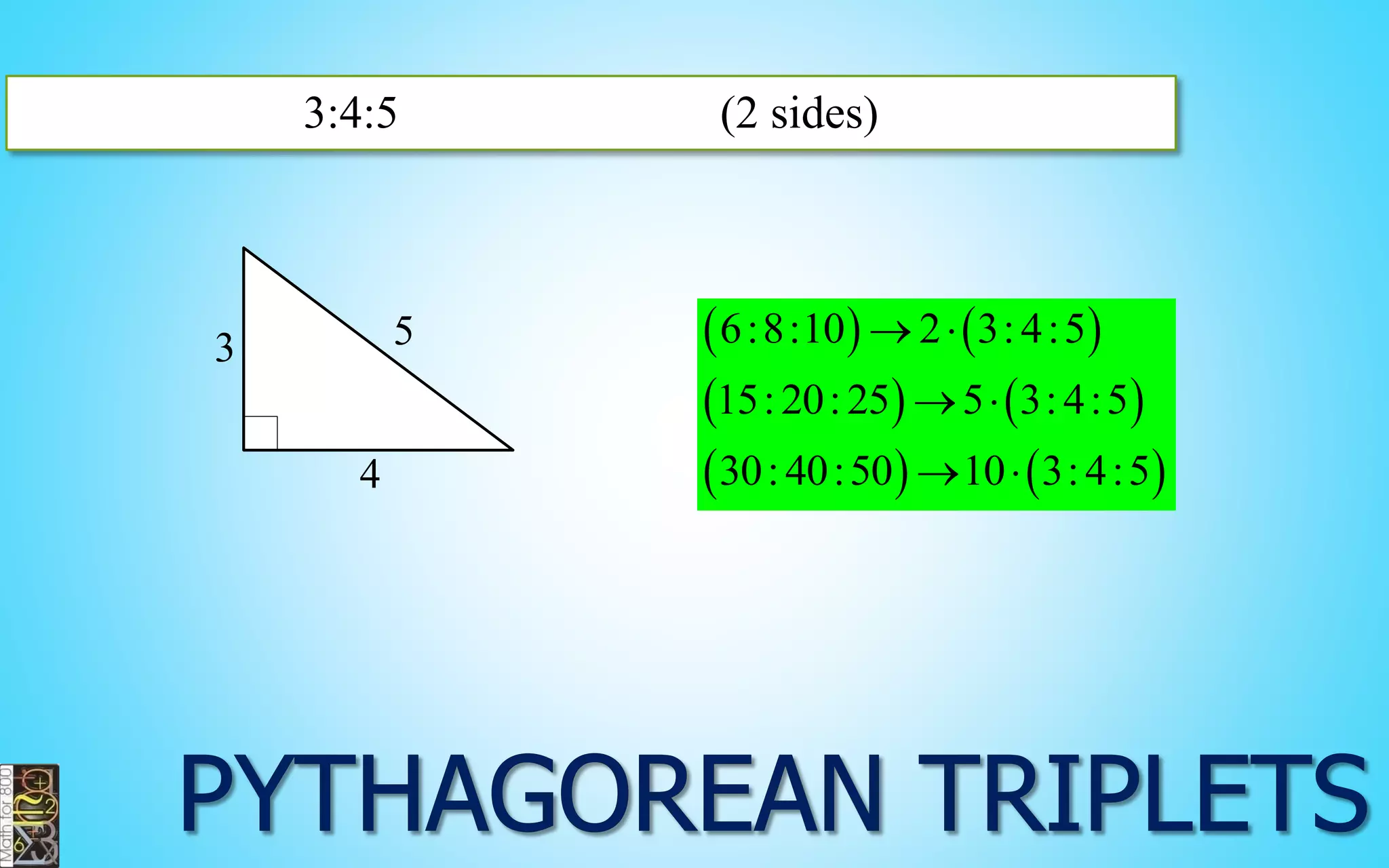
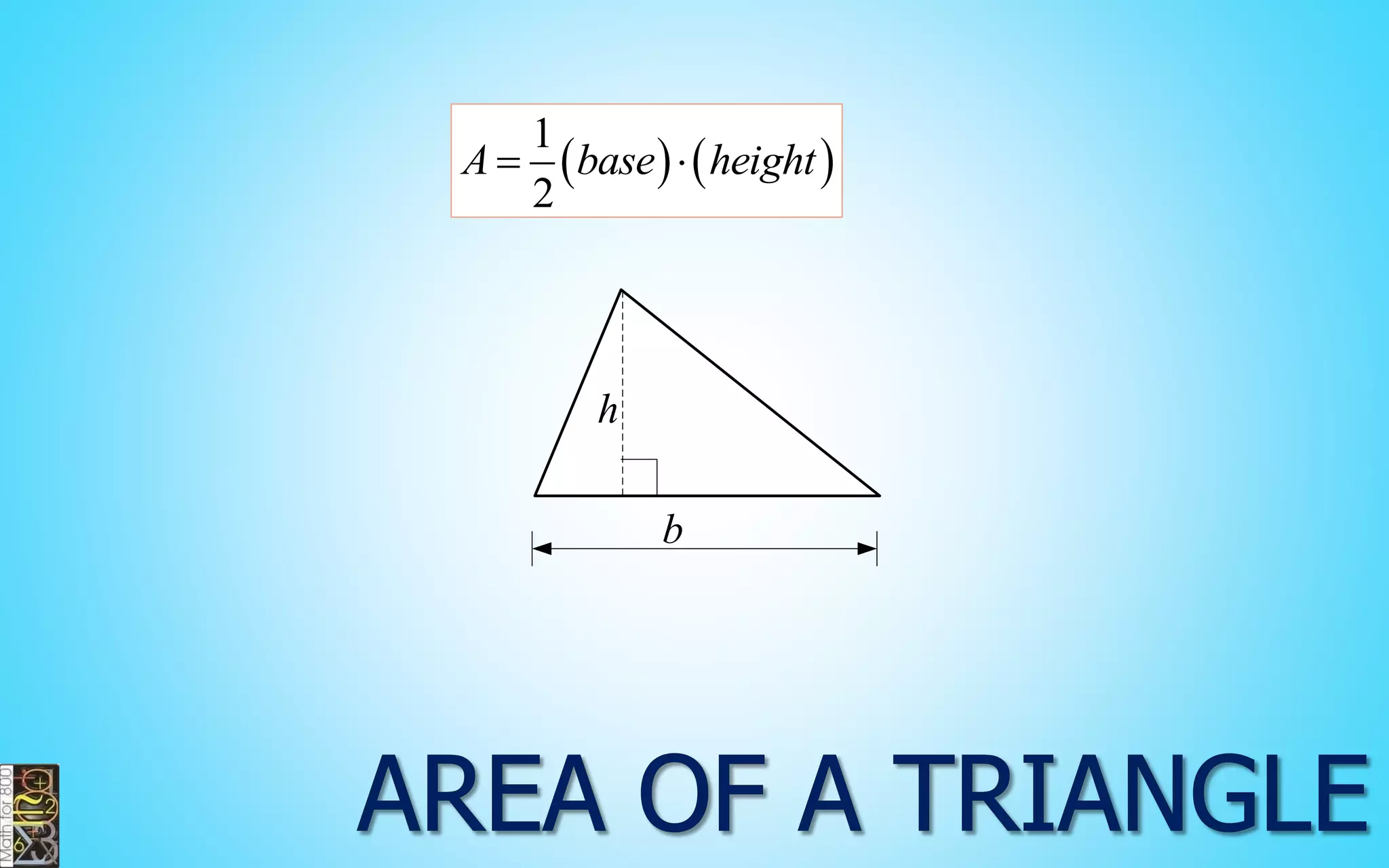
This document contains information about lines, angles, triangles, and calculating area of triangles. It defines key concepts such as parallel lines, perpendicular lines, angle measurements, different types of triangles, properties of triangles including angle sums and side lengths, calculating midsegments, similarity of triangles, and using base and height to calculate the area of triangles. It provides examples and explanations of geometric rules and formulas.

2. edwinxav@hotmail.com
elapuerta@hotmail.com

5. Two points determine a
straight line.
AB

6. Is a segment that is extended
infinitely in one direction.
AB

7. Is a section of a straight line, of finite length with two endpoints.
AB

8. Is the distance between its endpoints.
10 3
7
AB 

3 10

9. If point Q is between point P and
point R, then
PQQR  PR

12. With a letter, a number, or
a group of three letters.
a
A
B C
Angle a Angle ABC

13. It is extremely unlikely that you’ll see any fractional angles (23 ½o). There are no negative angles (−30o).

14. Angles greater than zero but less than 90o.

15. Angles with measure equal to 90o.

16. Angles greater than 90obut less than 180o.

17. An angle that measures exactly 180o.

18. Two angles that sum up to 90o.

19. Two angles that sum up to 180o.

25. Edwin Lapuerta, May 2014

31. LINES AND ANGLES

33. Angles opposite each other when two lines cross.
acbdabcd  

34. Angles that have a common vertex
and share a side.
a
c
b
d
,
180
180
180
180
a b c d
a c
a d
b c
b d
 
 
 
 
 
a  b  c  d  360

35. ABC CBD
A
B
C
D
If BC is the angle bisector
of angle ABD, then

37. L1L2

39. Two lines which not meet.
L1
L2
L1 || L2

41. L1
L2
4 1
3 2
8 5
7 6
L1 || L2
1 3 5 7
2 4 6 8
small angles
big angles
      
     

42. L1
L2
4 1
3 2
8 5
7 6
L1 || L2
small angle  big angle  180

44. An angle is a right angle
only if:
 You’re expressly told, “this
is a right angle”.
You see the
perpendicular symbol ().
You see the box in the
angle.
L1
L2

46. TRIANGLES

47. A triangle with three equal sides and three equal angles (60o).

48. A triangle with two equal sides and two equal angles.

49. A triangle with no equal sides and no equal angles.

50. If two sides of a triangle are unequal, the angles opposite these sides are unequal.

51. If two angles of a triangle are unequal, the sides opposite these angles are unequal.

52. The largest angle is opposite to the largest side.

54. A triangle has 3 possible midsegments.
d
m
E
D
B
C
A

55. The midsegmentis always parallel to the third side of the triangle.
d
m
E
D
B
C
A

56. The midsegmentis always half of the length of the third side.
d
m
E
D
B
C
A12md

57. d
m
D E
B
A C
The triangle formed
by the midsegment
is similar to the
original triangle.
DBE ABC
DB EB DE
AB CB AC
 

58. 2a2b2cabc

59. CongurentTriangles
have exactly the same three sides and exactly the same three angles.

60. Corresponding sides and angles are equal .

61. SAS(Side-Angle-Side)

62. SSS (Side-Side-Side)

63. ASA (Angle-Side-Angle)

64. AAS (Angle-Angle-Side)

65. The sum of the lengths of the sides.
abcPabc

66. The sum of the length of two sides must be greater than the length of the third side.
a
b
c
abcbaccab   

67. The difference of two sides must be less than the third side.
a
b
cbcaacbabc   

68. a
b
cbcabcacbacabcab   

69. a
b
c
A
B
C
The sum of the length of two sides must be greater than the length of the third side.
+

70. In any triangle, the sum of the interior
angles is 180o.
a b
c A B
C
A B C 180

71. The largest side is the hypotenuse and the
sides adjacent to the right angle (C = 90o) are
the legs.
C A
B
a
c
b
180
90
A B C
A B
  
 

72. The measure of exterior angles of a triangle
is equal to the sum of the two remote
interior angles.
a
b
c
y
x
z
360
x b c
y a c
z a b
x y z
 
 
 
  

73. The square of the length of the hypotenuse
is equal to the sum of the squares of the
lengths of the legs of the triangle.
a
b
c
2 2 2 a  b  c
It works only in right triangles.

74. 3:4:5 (2 sides)
5
4
3    
   
   
6:8:10 2 3: 4:5
15: 20: 25 5 3: 4:5
30: 40:50 10 3: 4:5
 
 
 

75. 5:12:13 (2 sides)
13
12
5
   
   
   
10: 24: 26 2 5:12:13
25:60:65 5 5:12:13
50:120:130 10 5:12:13
 
 
 

76. Isosceles right triangle 1:1:1 2  (1 side)
x
x x 2
45o
45o
   
   
   
: : 2 1:1:1 2
2: 2: 2 2 2 1:1:1 2
5:5:5 2 5 1:1:1 2
x x x x 
 
 

77. 1: 3 : 2 (1 side)
x 2x
x 3
30o
60o    
   
   
: 3 : 2 1: 3 : 2
2: 2 3 : 4 2 1: 3 : 2
5:5 3 :10 5 1: 3 : 2
x x x x 
 
 

78.    
1
2
A  base  height
The term "base" denotes any side, and
"height" denotes the length of a
perpendicular from the vertex opposite
the side onto the line containing the
side itself.

79.    
1
2
A  base  height
h
b

80.    
1
2
A  base  height
h
b

81.    
1
2
A  base  height
h
b

84. edwinxav@hotmail.com
elapuerta@hotmail.com