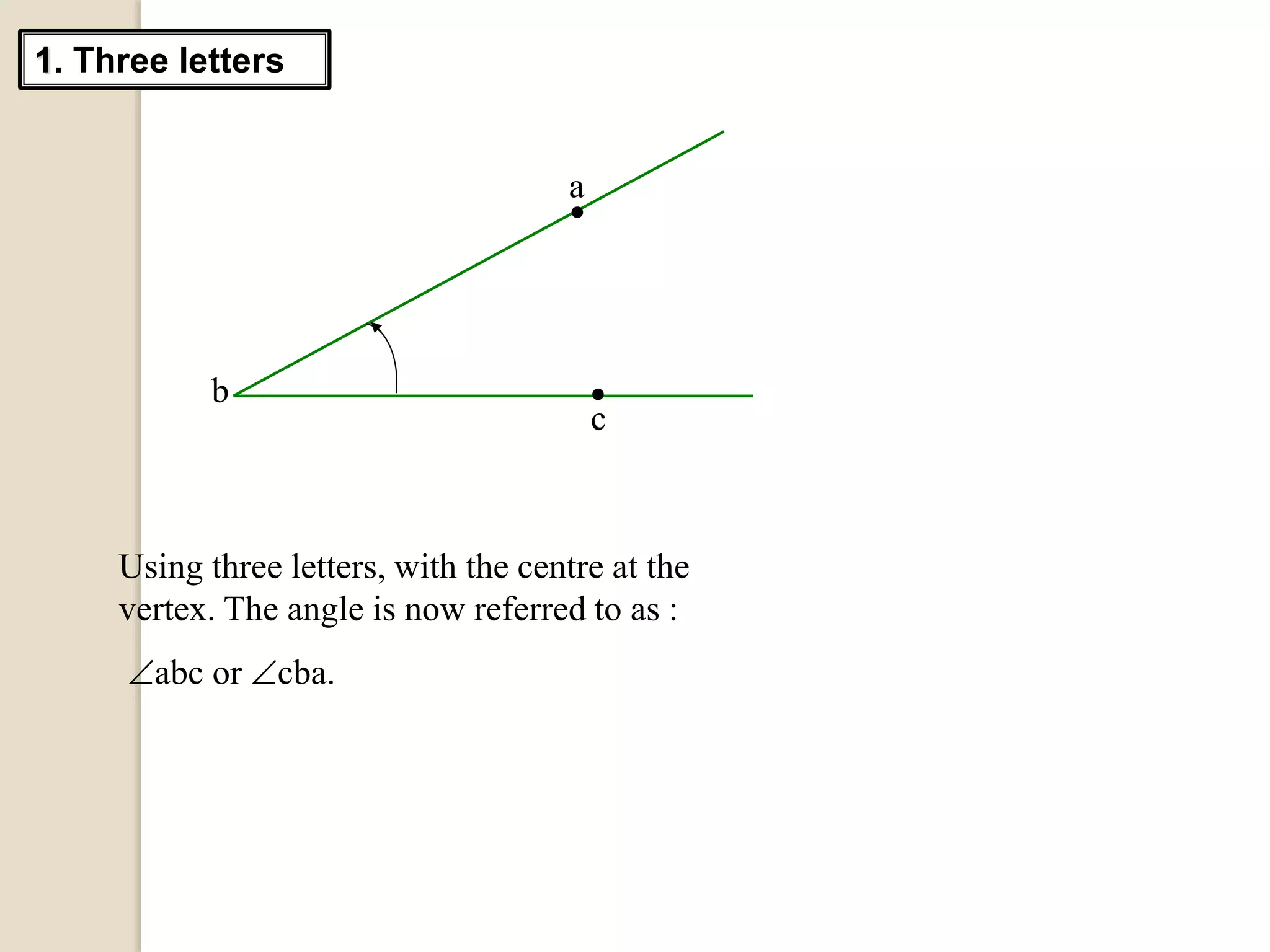
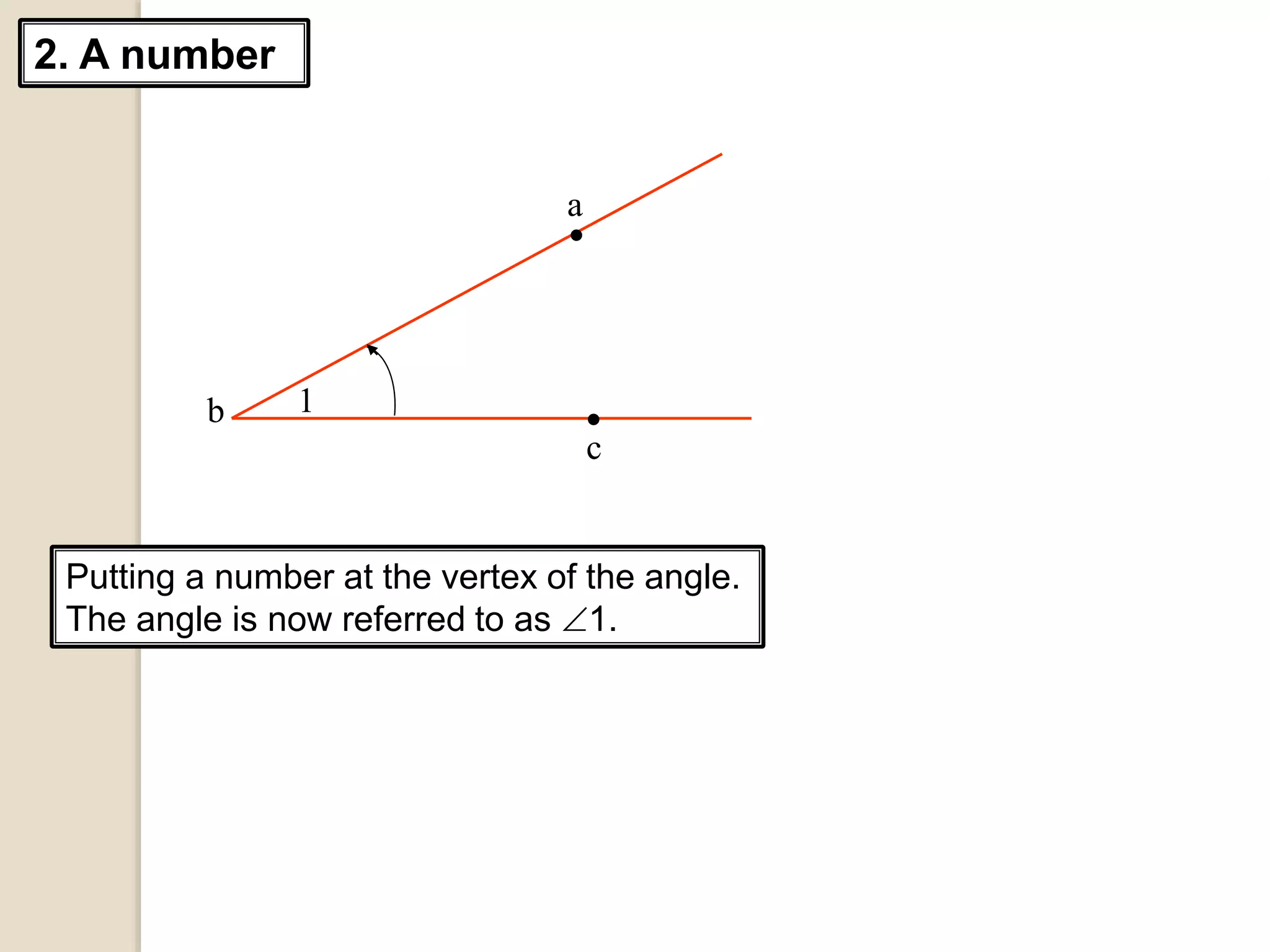
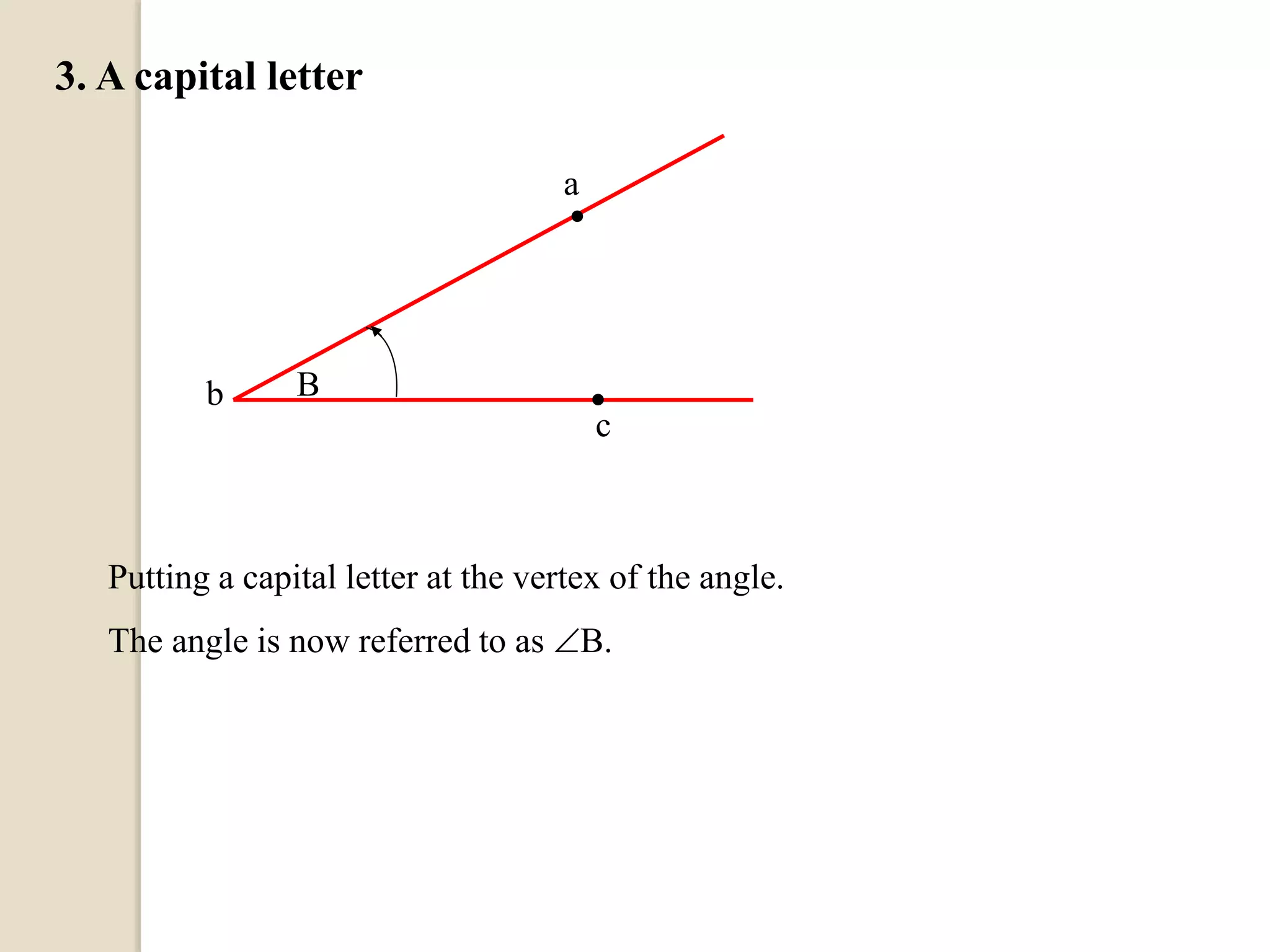
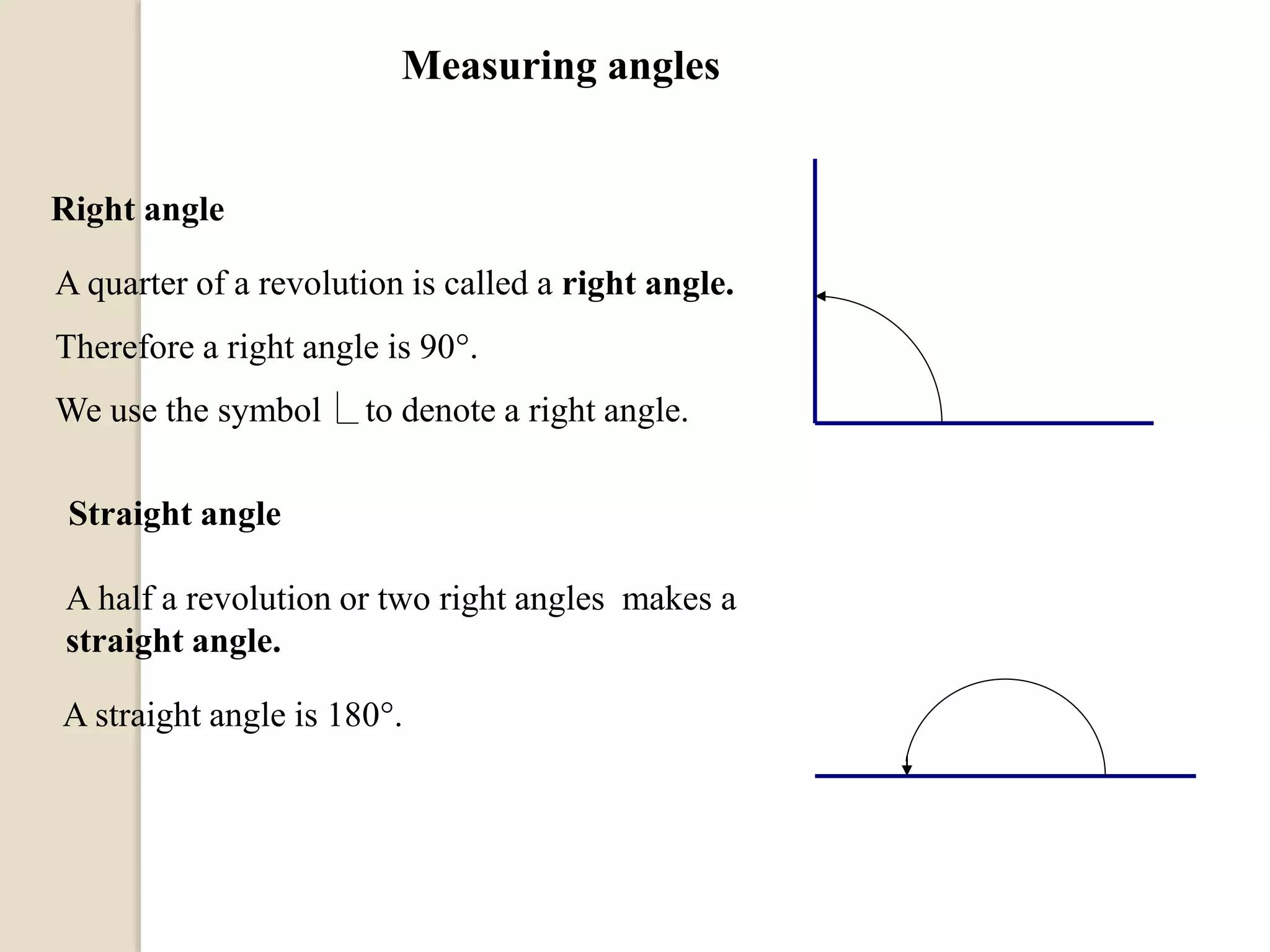
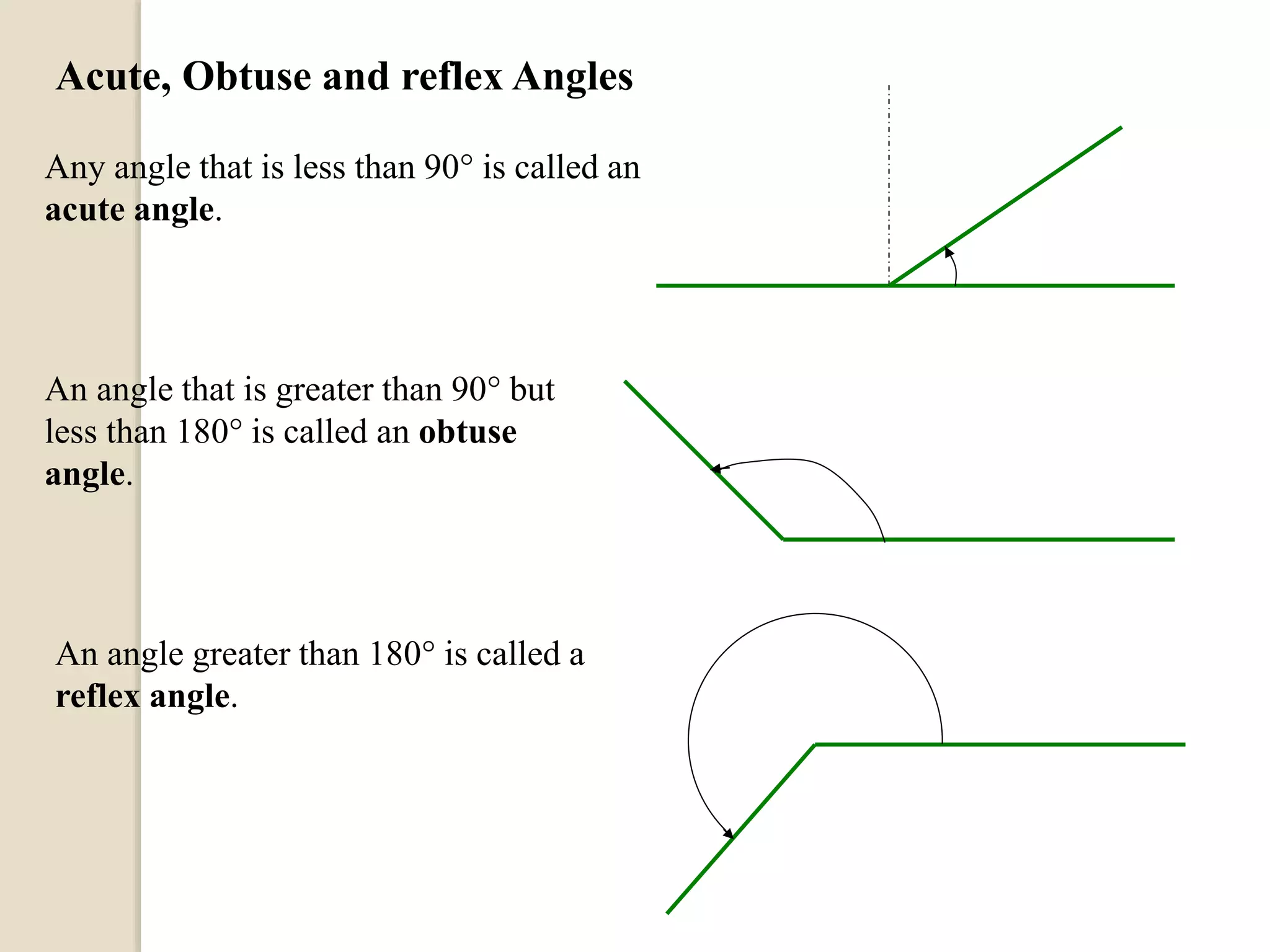
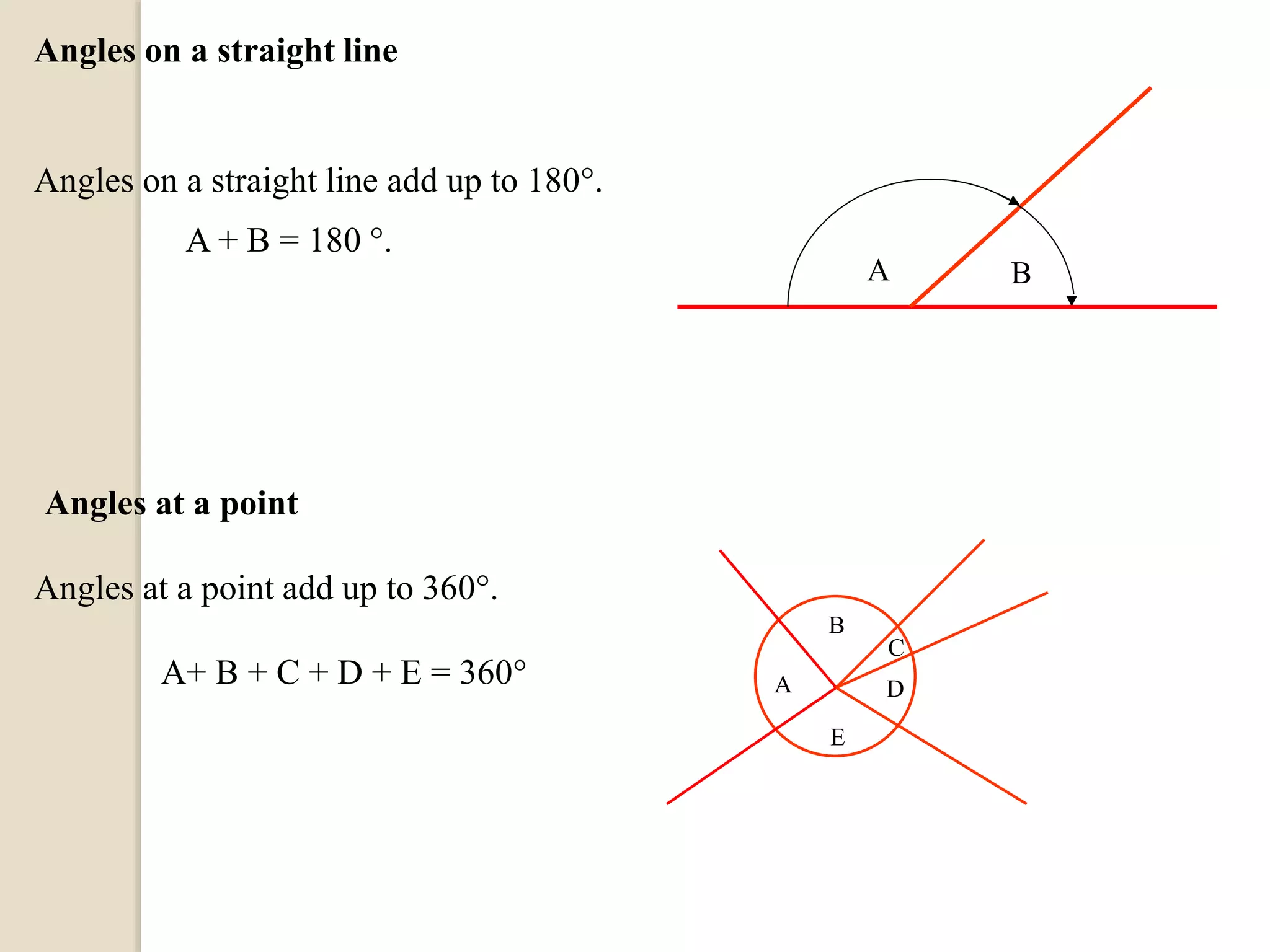
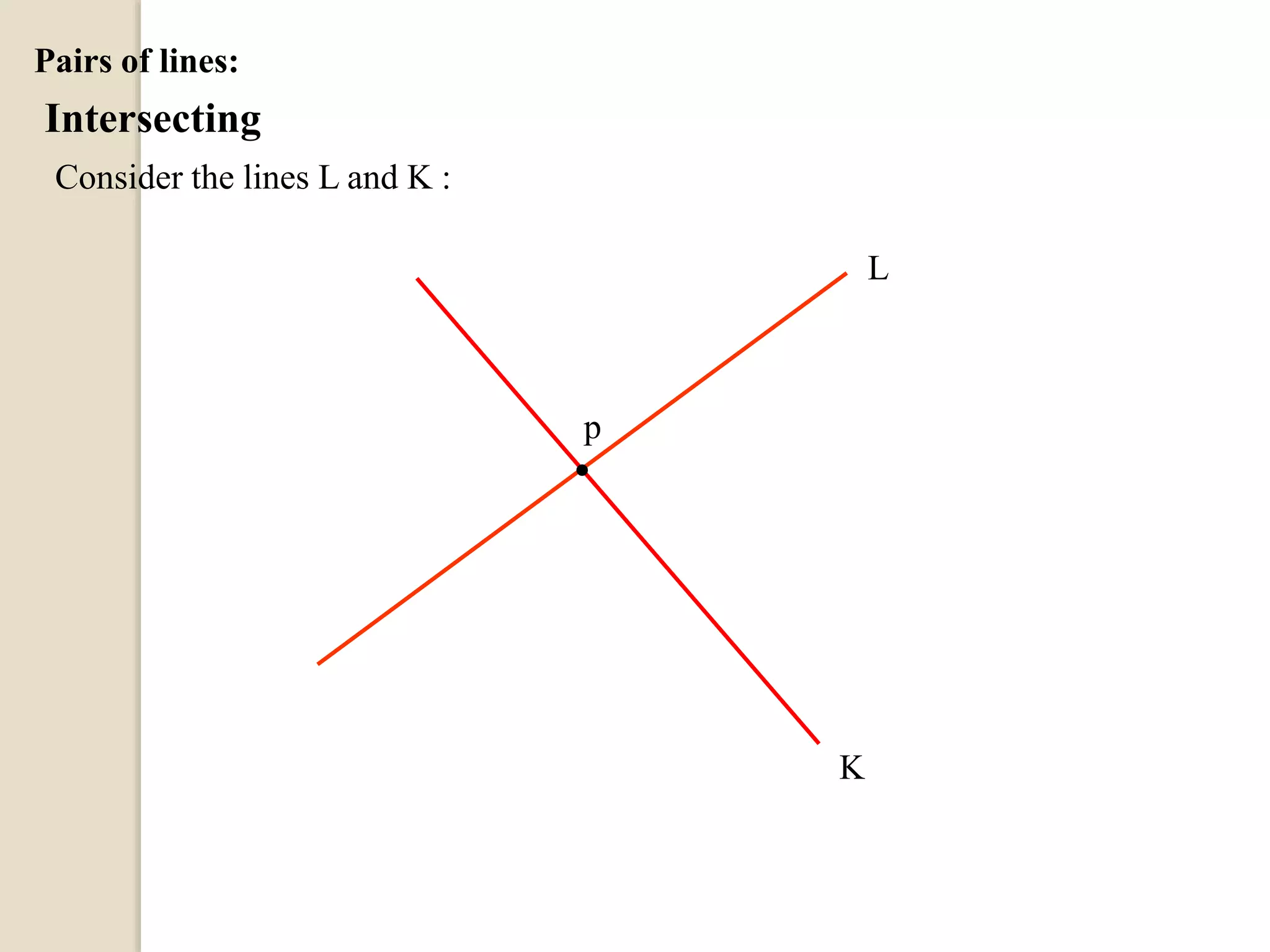
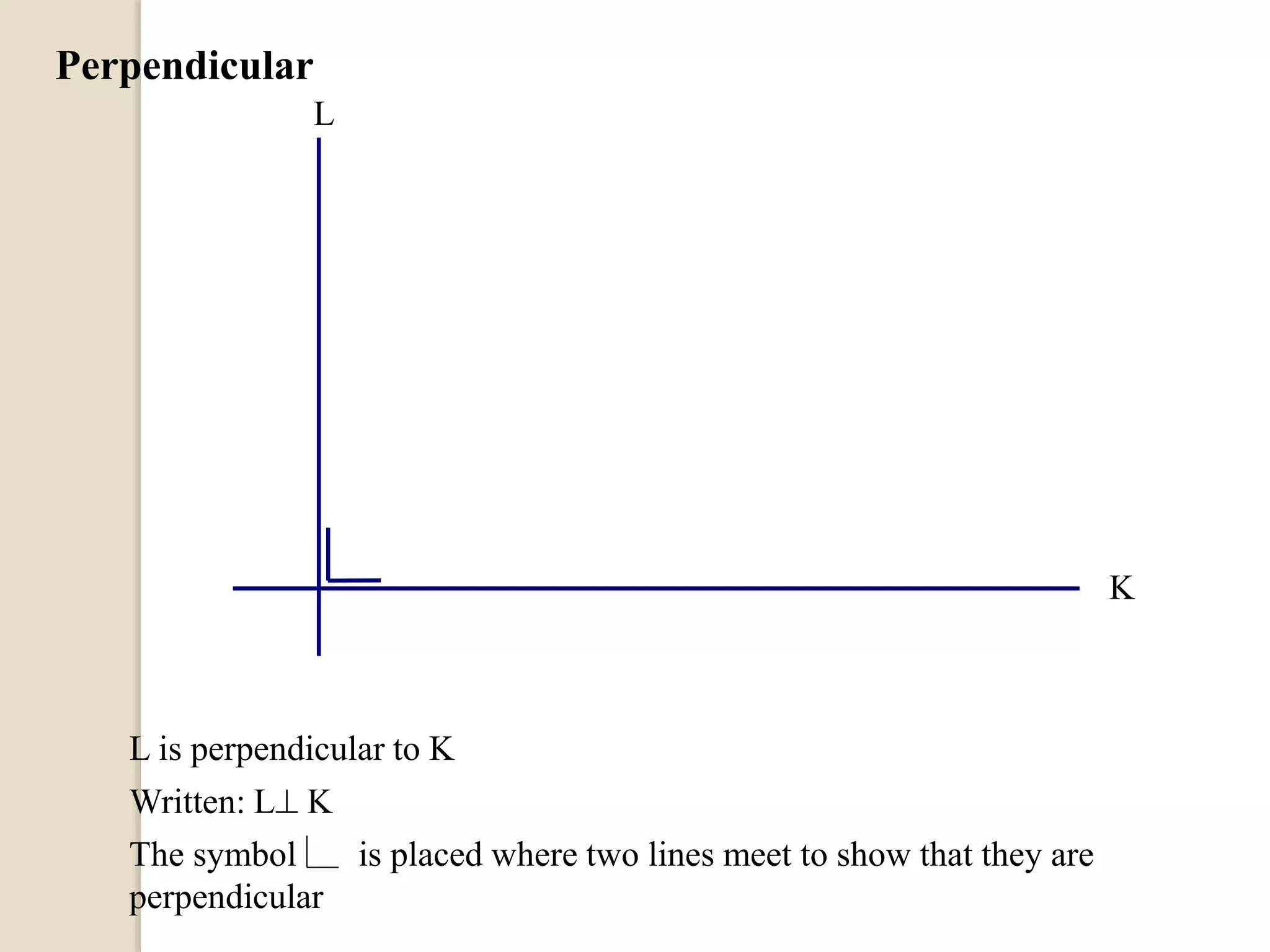
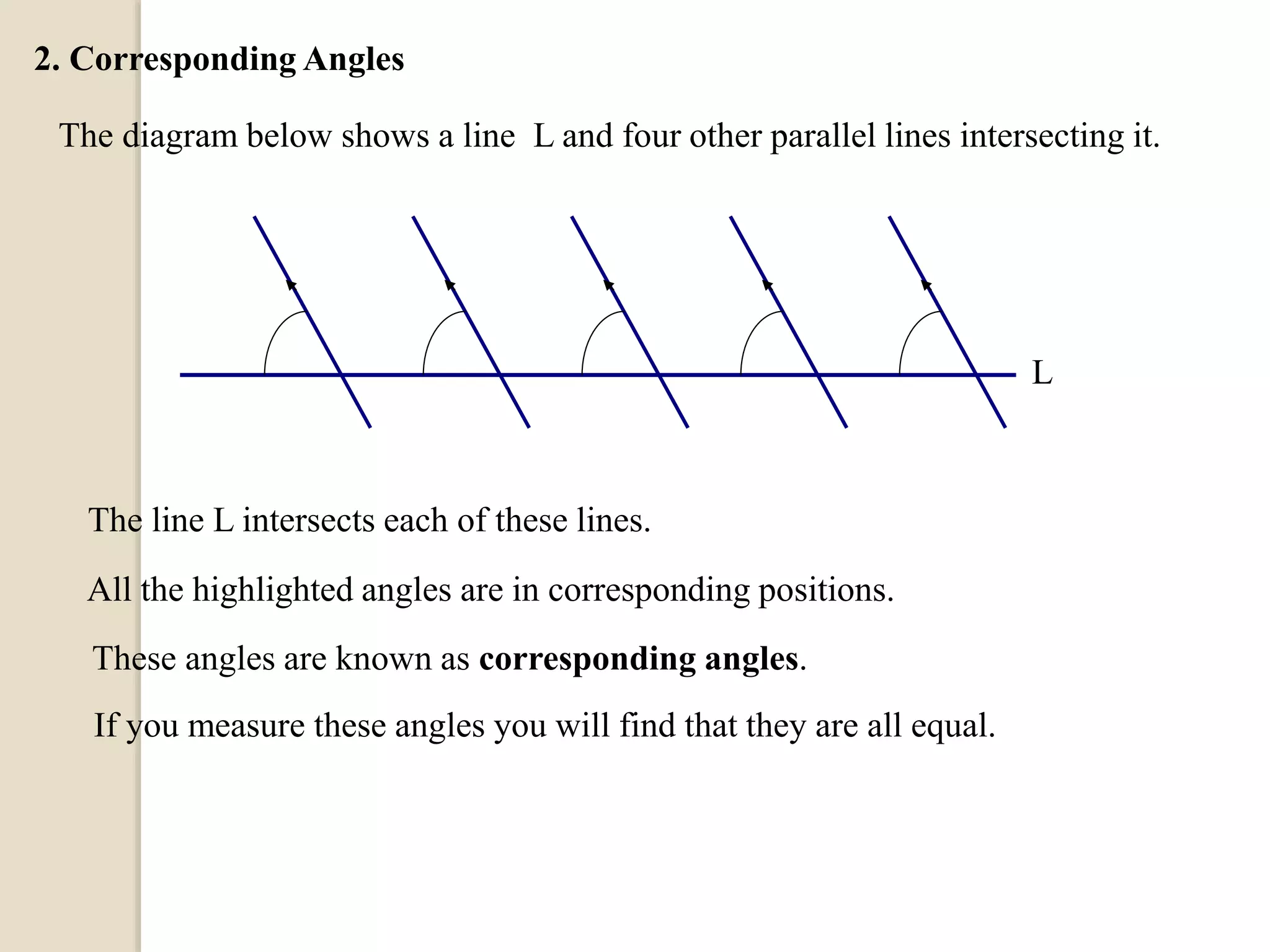
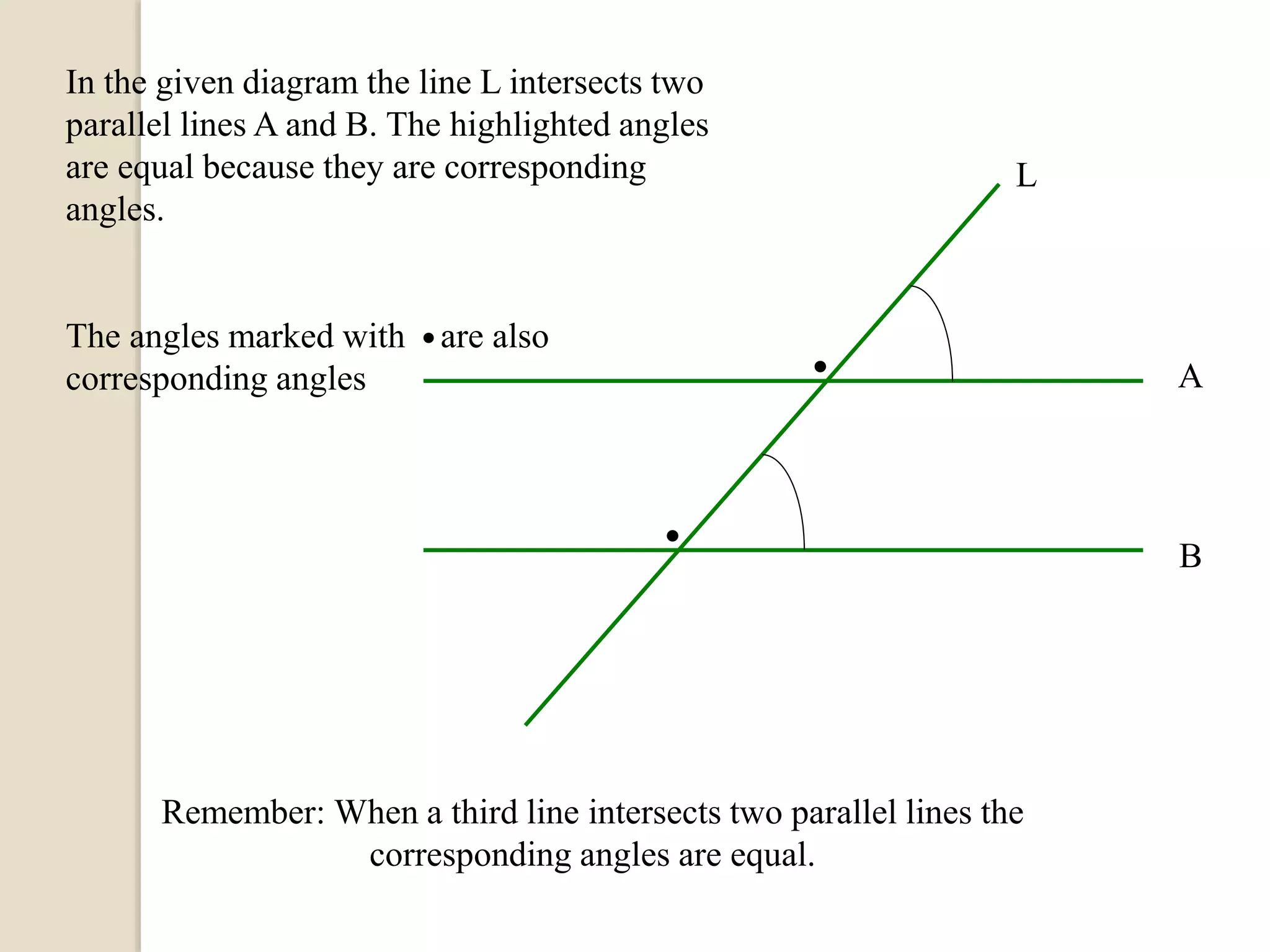
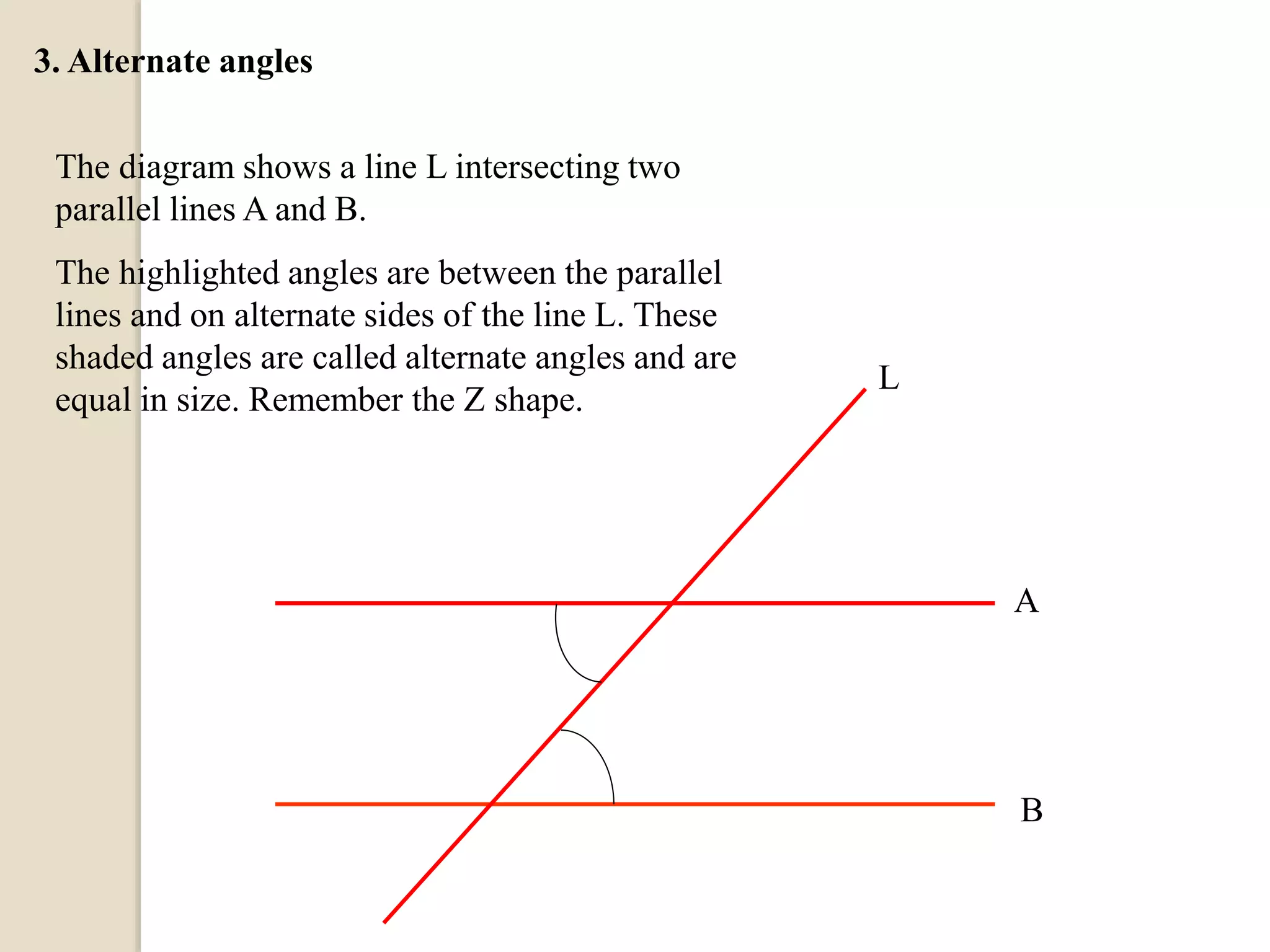
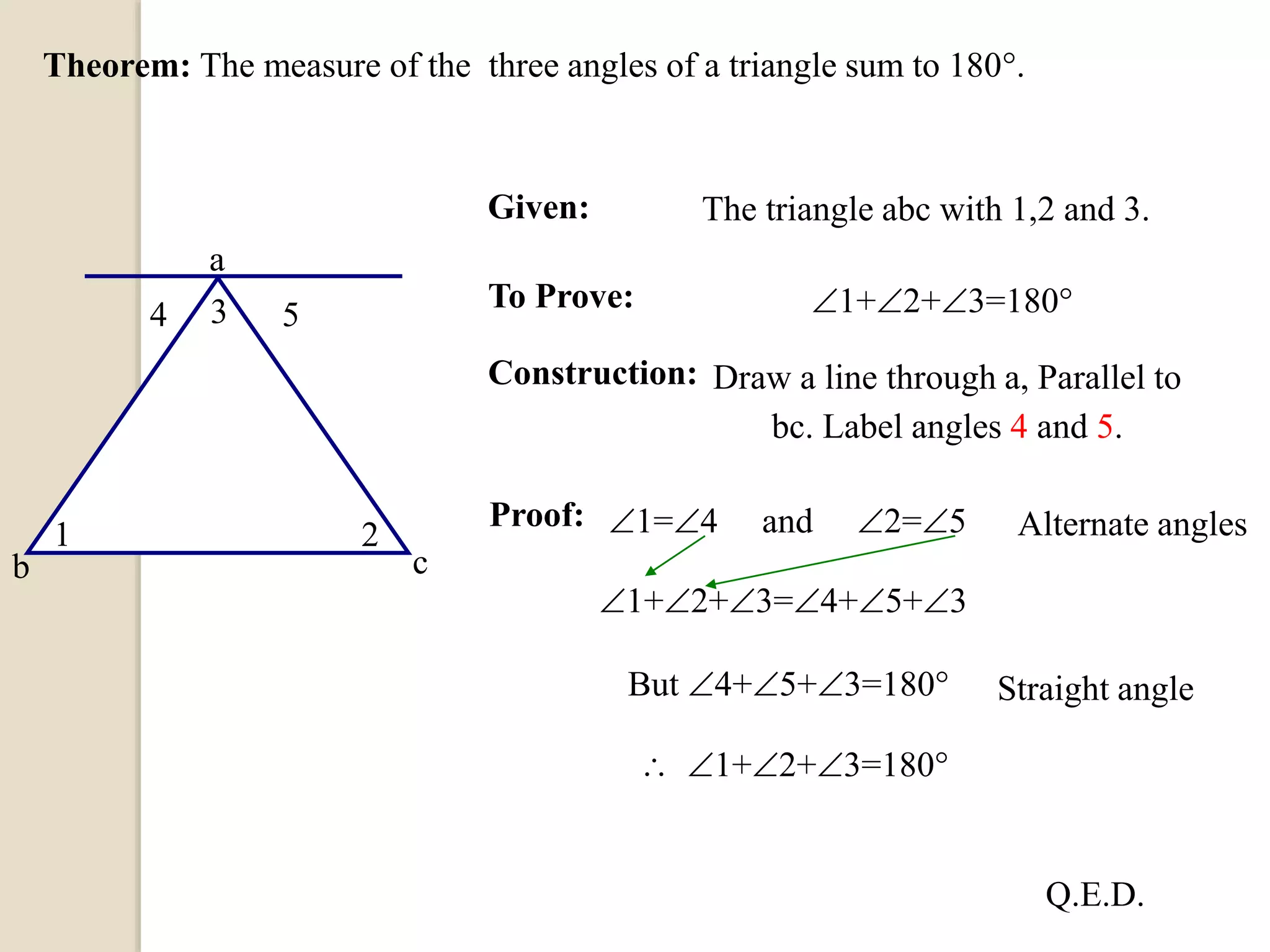
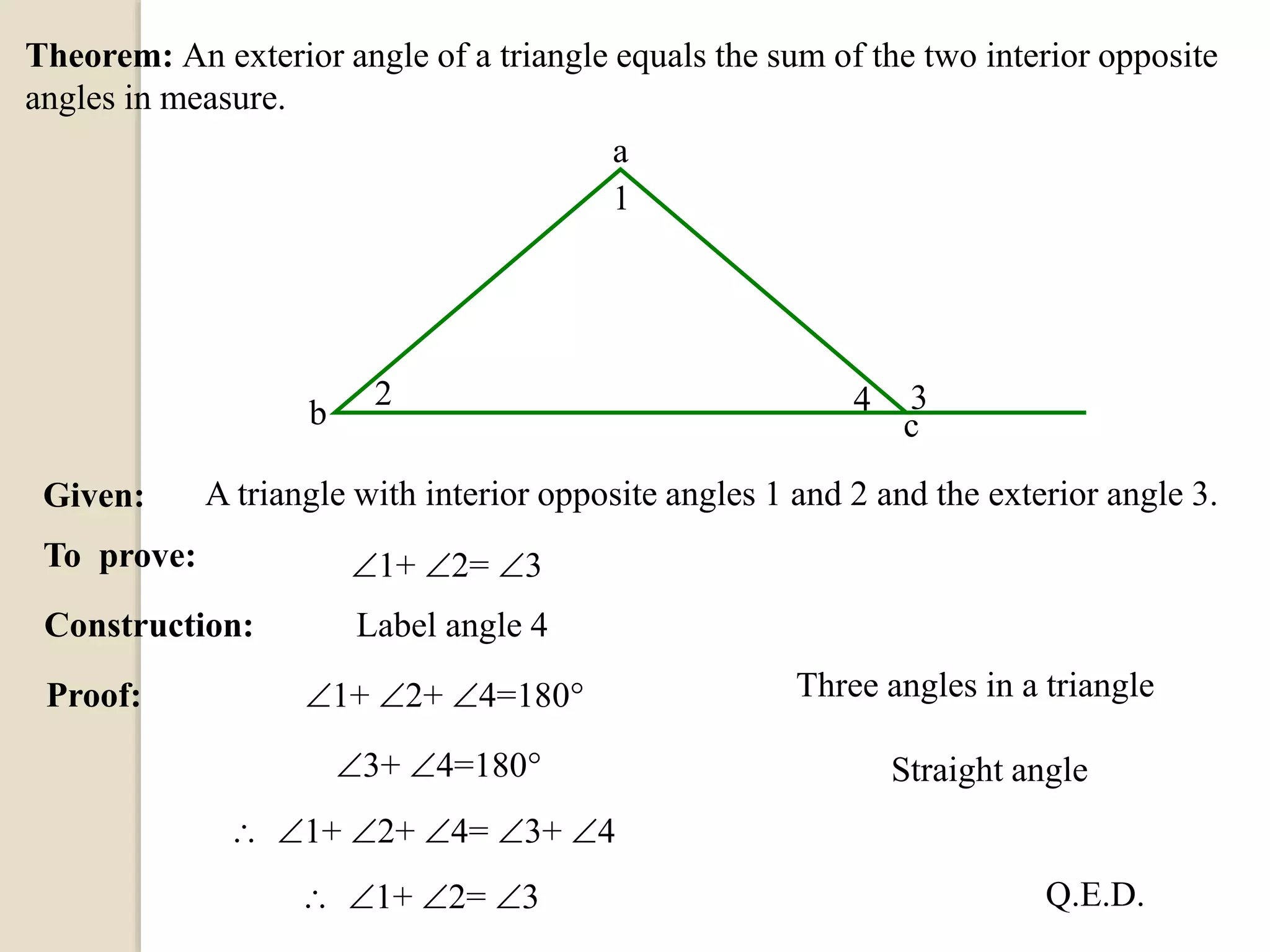
The document defines different types of angles and their properties. It explains what an angle is, how angles are named and measured. It discusses right angles, straight angles, acute angles, obtuse angles and reflex angles. It describes angles on a straight line, angles at a point, intersecting lines, parallel lines, perpendicular lines, vertically opposite angles, corresponding angles and alternate angles. It presents proofs of several theorems regarding the sum of interior and exterior angles of triangles.

1. Angle and Properties
For class VII
Prepared by
GOlam Robbani Ahmed

2. Angles
An angle is formed when two lines meet. The size
of the angle measures the amount of space
between the lines. In the diagram the lines ba and
bc are called the ‘arms’ of the angle, and the point
‘b’ at which they meet is called the ‘vertex’ of the
angle. An angle is denoted by the symbol  .An
angle can be named in one of the three ways:
a
c
b
.
.Amount of space
Angle

3. 1. Three letters
a
b
c
.
.
Using three letters, with the centre at the
vertex. The angle is now referred to as :
abc or cba.

4. 2. A number
c
b
.
.1
a
Putting a number at the vertex of the angle.
The angle is now referred to as 1.

5. 3. A capital letter
b
.
.B
a
c
Putting a capital letter at the vertex of the angle.
The angle is now referred to as B.

6. Right angle
A quarter of a revolution is called a right angle.
Therefore a right angle is 90.
Straight angle
A half a revolution or two right angles makes a
straight angle.
A straight angle is 180.
Measuring angles
We use the symbol to denote a right angle.

7. Acute, Obtuse and reflex Angles
Any angle that is less than 90 is called an
acute angle.
An angle that is greater than 90 but
less than 180 is called an obtuse
angle.
An angle greater than 180 is called a
reflex angle.

8. Angles on a straight line
Angles on a straight line add up to 180.
A + B = 180 .
Angles at a point
Angles at a point add up to 360.
A+ B + C + D + E = 360
A B
A
B
D
E
C

9. Pairs of lines:
Consider the lines L and K :
.p
L
K
Intersecting

10. Parallel lines
L
K
L is parallel to K
Written: LK
Parallel lines never meet and are usually indicated by arrows.
Parallel lines always remain the same distance apart.

11. Perpendicular
L is perpendicular to K
Written: L K
The symbol is placed where two lines meet to show that they are
perpendicular
L
K

12. Parallel lines and Angles
1.Vertically opposite angles
When two straight lines cross, four
angles are formed. The two angles that
are opposite each other are called
vertically opposite angles. Thus a and b
are vertically opposite angles. So also
are the angles c and d.
From the above diagram:
AB
C
D
A+ B = 180 …….. Straight angle
B + C = 180 ……... Straight angle
A + C = B + C ……… Now subtract c from both sides
A = B

13. 2. Corresponding Angles
The diagram below shows a line L and four other parallel lines intersecting it.
The line L intersects each of these lines.
L
All the highlighted angles are in corresponding positions.
These angles are known as corresponding angles.
If you measure these angles you will find that they are all equal.

14. In the given diagram the line L intersects two
parallel lines A and B. The highlighted angles
are equal because they are corresponding
angles.
The angles marked with are also
corresponding angles
. A
B
L
.
.
Remember: When a third line intersects two parallel lines the
corresponding angles are equal.

15. 3. Alternate angles
The diagram shows a line L intersecting two
parallel lines A and B.
The highlighted angles are between the parallel
lines and on alternate sides of the line L. These
shaded angles are called alternate angles and are
equal in size. Remember the Z shape.
A
B
L

16. Theorem: Vertically opposite angles are equal in measure.
Given:
To prove :
Construction:
Proof: Straight angle
Straight angle
 1=2
Label angle 3
1=2
Intersecting lines L and K, with vertically
opposite angles 1 and 2.
1+3=180
2+3=180
Q.E.D.
L
K
1 2
 1+3=3+2 .....Subtract 3 from both sides
3

17. Theorem: The measure of the three angles of a triangle sum to 180.
Given:
To Prove: 1+2+3=180
Construction:
Proof: 1=4 and 2=5 Alternate angles
1+2+3=4+5+3
But 4+5+3=180 Straight angle
 1+2+3=180
The triangle abc with 1,2 and 3.
4 5
a
b c
1 2
3
Q.E.D.
Draw a line through a, Parallel to
bc. Label angles 4 and 5.

18. Theorem: An exterior angle of a triangle equals the sum of the two interior opposite
angles in measure.
Given: A triangle with interior opposite angles 1 and 2 and the exterior angle 3.
To prove: 1+ 2= 3
Construction: Label angle 4
Proof: 1+ 2+ 4=180
3+ 4=180
Three angles in a triangle
 1+ 2+ 4= 3+ 4
Straight angle
 1+ 2= 3
a
b c
3
1
2 4
Q.E.D.