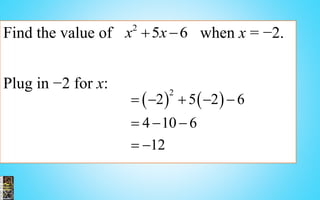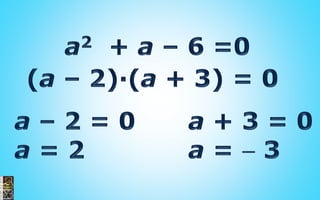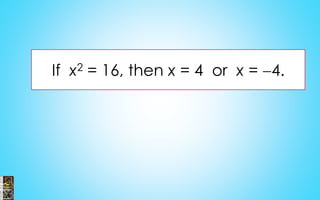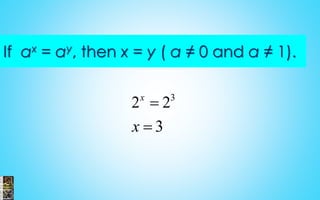1) The document discusses algebraic expressions and operations involving terms, monomials, polynomials, binomials, trinomials, and rational expressions. It also covers evaluating expressions, adding, subtracting, multiplying and dividing algebraic expressions.
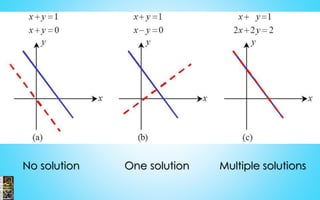
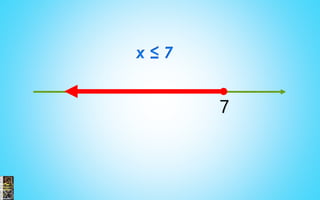
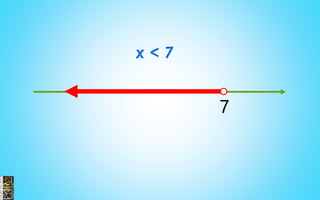
2) Procedures for solving equations, systems of equations, and inequalities are presented. This includes isolating variables, using substitution and elimination methods, solving quadratic and exponential equations, and determining the properties of roots.
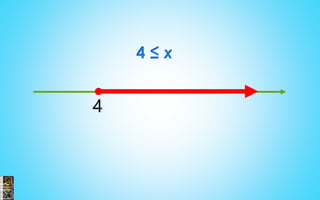
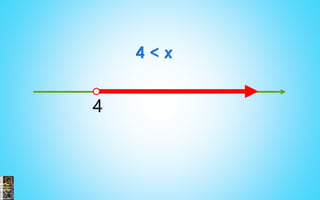
3) Examples are provided to illustrate solving linear, quadratic and rational equations as well as solving and graphing inequalities.