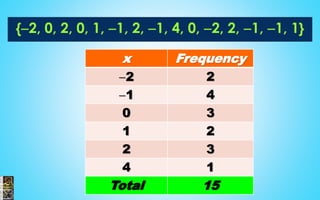
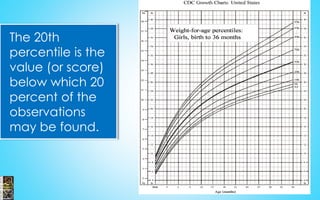
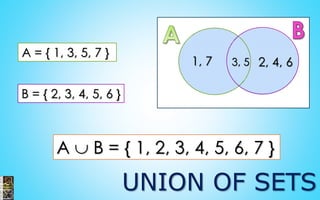
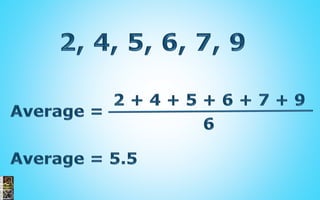- The document contains information about statistics including measures of central tendency, dispersion, probability, and counting methods.
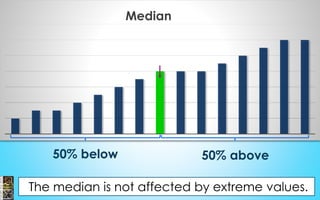
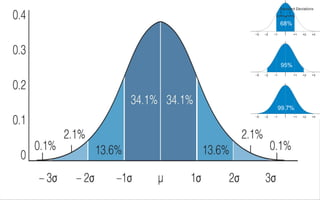
- It discusses topics like mean, median, mode, range, standard deviation, normal distribution, and the empirical rule.
- Probability concepts covered include independent and dependent events, the addition law of probabilities, and examples of calculating probabilities of various card draws.
- The final section discusses counting principles for permutations, combinations, and probability.