Uploaded byKareem Hossam
Material science 2
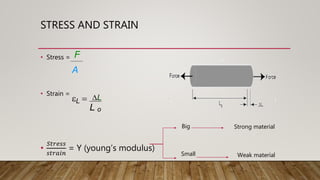
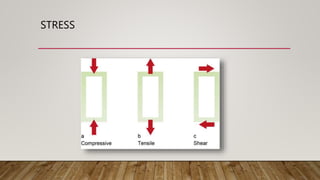
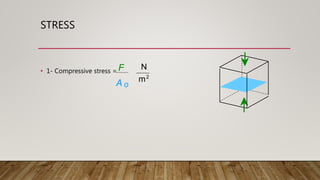
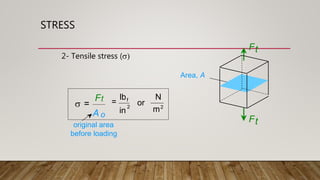
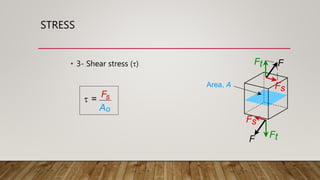
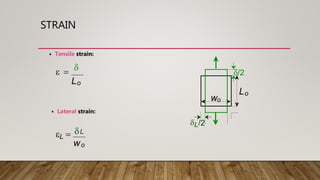
1) The document discusses various types of stress and strain including tensile stress, compressive stress, shear stress, tensile strain, and lateral strain. It defines stress as force over area and strain as the change in length over original length. 2) Young's modulus is defined as the ratio of stress to strain. Several examples are provided to demonstrate calculating stress, strain, and Young's modulus given different loading conditions and material properties. 3) Maximum stress that a material can withstand before breaking is discussed as well as an example of calculating the maximum weight a wire can support before breaking. 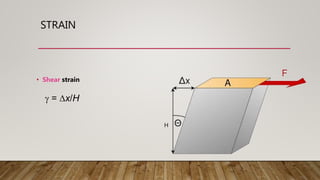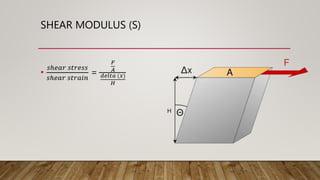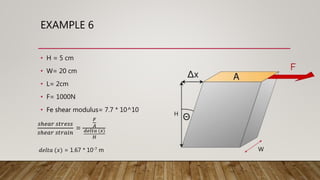4) Shear stress and modulus are defined and an example of calculating shear stress is given. 5) Bulk
More Related Content
Material science 2
- 1. MATERIAL SCIENCE ENG. KAREEM.H. MOKHTAR
- 2. STRESS AND STRAIN •Stress = • Strain = • 𝑆𝑡𝑟𝑒𝑠𝑠 𝑠𝑡𝑟𝑎𝑖𝑛 = Y (young’s modulus) F A eL = DL L o Big Small Weak material Strong material
- 3.
- 4. STRESS • 1- Compressivestress = F A o 2 m N
- 5. STRESS original area before loading Area,A Ft Ft s = Ft A o 2 f 2 m N or in lb = 2- Tensile stress (s)
- 6. STRESS • 3- Shearstress (t) Area, A Ft Ft Fs F F Fs t = Fs Ao
- 7. STRAIN e = d Lo d/2 dL/2 Lo wo •Lateral strain: eL = L wo d • Tensile strain:
- 8. STRAIN • Shear strain g= Dx/H H
- 9.
- 10. EXAMPLE 1 Givens Weight =1000N Area of the beam is 2cm x 2cm Lo = 1.75 m Find delta L Material Fe youngs modulus 𝑆𝑡𝑟𝑒𝑠𝑠 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 𝐿 𝐿𝑜 = 1000 2 𝑥 2 𝑥 10−4 ? 1.75 D
- 11. EXAMPLE 2 F Givens Weight= 50Kg Radius of the heel= 0.5 cm 30% of the woman's weight acts on the heel Solution • stress = F A o = 50 ∗ 0.3 ∗ 9.8 𝑝𝑖 4 ∗ 0.012 = 1871662 𝑁/𝑚2
- 12. EXAMPLE 4 Givens D= 1mm Lo=4m m= 500 kg Find the elongation young’s modulus (AL) = 7 * 10^10 N/m2 Solution young’s modulus= 𝑆𝑡𝑟𝑒𝑠𝑠 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 𝐿 𝐿𝑜 = 500∗9.8 𝑝𝑖 4 ∗ 10−6 ? 4 = 6.9* 1010
- 13. MAX STRESS (BREAKINGSTRESS) • It is the max stress a material can handle before it breaks
- 14. EXAMPLE 3 • Wouldthe wire breaks or not? • F/ A = 500 * 9.8 / pi*0.0005^2 • What is the maximum weight this wire could handle • StressMAX = mmax* g / A Mmax= 17.6 kg
- 15. SHEAR MODULUS (S) • 𝑠ℎ𝑒𝑎𝑟𝑠𝑡𝑟𝑒𝑠𝑠 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 𝑑𝑒𝑙𝑡𝑎 (𝑥) 𝐻 H
- 16. SHEAR STRESS • Itis used in cutting materials • The area used is the area that is going to be cut
- 17. EXAMPLE 6 • H= 5 cm • W= 20 cm • L= 2cm • F= 1000N • Fe shear modulus= 7.7 * 10^10 W H 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑒𝑠𝑠 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 𝑑𝑒𝑙𝑡𝑎 (𝑥) 𝐻 𝑑𝑒𝑙𝑡𝑎 (𝑥) = 1.67 * 10-7 m
- 18. EXAMPLE 8 Givens The diameterof the drilling bit= 4.2 cm Thickness of the sheet = 5mm Length of the sheet = 5 m Width of the sheet = 3 m Shear stress of steel = 4 x 10^8 Solution Shear stress= F/A F= 4 *10^8 * pi * 0.042*0.005 = 263893.8 N
- 19. BULK MODULUS 𝐵𝑢𝑙𝑘 𝑠𝑡𝑟𝑒𝑠𝑠 𝐵𝑢𝑙𝑘𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 − 𝑑𝑒𝑙𝑡𝑎 (𝑣) 𝑉𝑜 Compressibility = 1 𝐵𝑢𝑙𝑘 𝑚𝑜𝑑𝑢𝑙𝑢𝑠 The higher the bulk modulus the more force you need to Change the volume of the material
- 20. EXAMPLE 6 • ABowling ball made of steel sunk in an ocean, find the change in it’s volume if you know that the ocean is 10000 m in depth and the original volume of the ball is 1m^3 𝐵𝑢𝑙𝑘 𝑠𝑡𝑟𝑒𝑠𝑠 𝐵𝑢𝑙𝑘 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹 𝐴 𝑑𝑒𝑙𝑡𝑎 (𝑣) 𝑉𝑜 = Bulk modulus