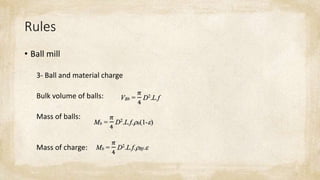1) Rittinger's law and Bond's law are used to calculate the time required to increase the specific surface area of a rock being crushed by 30%. The calculated time is 59 minutes. 2) Using the given work index, the theoretical power required to grind one ton of a material in a roller mill over 30 minutes is estimated to be 10 horsepower. 3) For a batch ball mill with given dimensions, specifications of the grinding media, and void ratios: (a) the recommended speed of revolution is 25 RPM, (b) the recommended charge of alumina balls is 1.7 tons, (c) the recommended charge of limestone is 679.9 kg.

1. Common Mechanical Operation
Section 5
Eng. Kareem H. Mokhtar

2. Rules
• Rittinger’s law
• Kick’s law
• Bond
• Db: at cumulative = 0.2

3. Rules
• Crushing rolls
• Ball mill
• 1- rotation speed
N: RPM, D: Mill diameter , d: ball diameter , Actual speed 65-75%
D: roll diameter, D2 : product diameter, D1: feed diameter

4. Rules
• Ball mill
2- Size of balls (db : ball diameter, mm & Db2: Bond diameter of the product)

5. Rules
• Ball mill
3- Ball and material charge
Bulk volume of balls:
Mass of balls:
Mass of charge:

6. Question 1
• Rock lumps equivalent to 2” spheres are crushed in a batch hammer
crusher run at constant power. If it takes 45 minutes to reduce the
feed to the screen analysis shown below, calculate the time required
to increase the specific surface by 30%, using Rittinger’s equation.
D mm 4.699 2.362 1.168 0.833 0.417 0.295 0.208 pan
xi 0.00 0.15 0.30 0.25 0.15 0.10 0.05 0.00

7. Answer 1
• Rittinger’s equation
• Dvs1 = 0.0508 m
• To get Dvs2
•
1
𝐷𝑣𝑠
=
𝑋𝑖
𝐷𝑝 𝑎𝑣
• Dvs2 = 0.00085 m
• (P/mk)*45 = 1156.8  (P/mk) = 25.7

8. • (P/mk)*t2 = (1/Dv3 – 1/Dv2)
• Sp. Area per unit volume =
𝑆𝑢𝑟𝑓𝑎𝑐𝑒 𝑎𝑟𝑒𝑎
𝑣𝑜𝑙𝑢𝑚𝑒
=
6 (𝑠ℎ𝑎𝑝𝑒 𝑓𝑎𝑐𝑡𝑜𝑟)
𝐷𝑝
• A3 = 1.3 A2  (1/Dvs3) = 1.3 (1/Dvs2)  Dvs3 = 0.00065 m
So t2 = 14 min
From the beginning = 45 + 14 = 59 min

9. Question 2
• The product from the previous crusher is finely ground using a roller
mill. The screen analysis of product is shown below. If the work index
is 12, estimate the theoretical power required to grind a one ton
batch in 30 minutes.
D mm 0.833 0.589 0.417 0.295 0.208 0.147 0.074 pan
xi 0.00 0.10 0.25 0.30 0.20 0.15 0.05 0.00

10. Answer 2
Workindex =12 , mass = 1 ton , time = 30 min
At cumulative = 0.2  Db1 = 2mm and Db2 = 0.5 mm
Dry process * 4/3
Pth = 7155 watt / 745.7 = 9.6 = 10 Hp

11. Question 3
• The length of a batch ball mill is equal to its diameter = 1.5 m. It uses 2”
diameter alumina balls to grind limestone pebbles. Estimate the following:
(a) A reasonable speed of revolution for the mill
(b) The charge of balls
(c) The rock feed charge
• Data:
• Specific gravity of alumina = 3
• Specific gravity of limestone = 2.85
• Porosity of ball charge = 0.45
• Percent voids between limestone particles = 50%

12. Answer
• Givens: L=D= 1.5m , alumina balls = 2”, density= 3000kg/m3
• Limestone density 2850 kg/m3
• Ball mill
• 1- rotation speed
• N= 35 RPM  actual RPM is 25 RPM
N: RPM, D: Mill diameter , d: ball diameter , Actual speed 65-75%

13. • B) Charge of ball
• 1.7 ton
• C) Charge of rock
• 679.9 kg

14. Question 4
• It is required to design a tube mill of length = 2.5 times the diameter
to grind crushed rock of bulk density = 1800 kg/m3 at a rate of 10 tons
per hour. To this aim, steel balls are used of void ratio = 0.5. It is
assumed that 40% of the mill will be occupied by balls and that the
charge will just fill the void space between balls. If the retention time
of rock stream inside the mill is 30 minutes, what are the dimensions
of the mill?
D= 2m and Length = 5 m

15. Question 5
• In the manufacture of water based paints, the ingredients (pigment +
adhesive) are suspended in water to form a slurry. The average
density of solids = 2300 kg/m3, and the solid content by weight is
25%. This slurry is to be ground in an available batch ball mill of
length = diameter = 1.25 m. Porcelain balls of 40 mm diameter are
used (Specific gravity = 2.6). They fill 50% of the mill and the void
ratio between these balls = 45%.
• Calculate the mass of slurry in the mill and the number of balls
required.

16. • To determine the mass of slurry
• The density of slurry:
• Assume 1 kg of slurry it will contain 0.25kg of solid and 0.75kg water
• Volume of solid= 0.25/2300 = 1.09 *10-4 m3
• Volume of water = 0.75/1000 = 7.5 *10-4 m3
• Density of slurry = mass/volume = 1/ (1.09 *10-4 + 7.5 *10-4 ) =
1164.65 kg/m3

17. • Mass of feed = (pi/4)*(1.25)2*1.25 * 0.5*1164.6*0.45 = 402 kg
• Mballs = 1096.8 kg
• To get the number of balls
• Total volume of balls = 1096.8/2600 = 0.42 m3
• Volume of one ball = (4/3)* pi* (0.02)3= 3.35 * 10-5 m3
• No. of balls = 0.42/(3.35 * 10-5 ) = 12537 balls