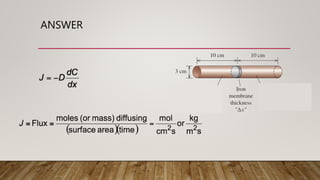
This document discusses diffusion through a membrane and solving related problems. It contains: 1) Information on Fick's first law of diffusion and the Arrhenius equation for calculating diffusion rates. 2) A sample problem calculating the number of nickel ions diffusing through MgO per second given parameters like thickness, temperature, and diffusion coefficient. 3) A multi-part problem designing an iron membrane thickness to allow less than 1% nitrogen loss per hour and 90% hydrogen passage per hour given gas concentrations and diffusion rates at 700C.

1. DIFFUSION-2
ENG. KAREEM H. MOKHTAR

2. ARRHENIUS EQUATION
• Rate = c e-E/RT
• Rate: rate of diffusion (m2/s
or jump per second)
• E: activation energy
• R: gas constant
• T: temperature
• ln(rate) = ln(c) – E/RT
• Straight line equation
Y= m x + cLn (rate)
1/T
Slope= -E/R

3. FICK’S FIRST LAW
• The rate at which atoms, ions, particles or other species diffuse in a material can
be measured by the flux J. Here we are mainly concerned with diffusion of ions
or atoms. The flux J is defined as the number of atoms passing through a plane
of unit area per unit time

4. SHEET 4
• Q6) 0.05 cm layer of magnesium oxide (MgO) is deposited between layers of
nickel (Ni) and tantalum (Ta) to provide a diffusion barrier that prevents reactions
between the two metals. At 1400°C, nickel ions diffuse through the MgO ceramic
to the tantalum. Determine the number of nickel ions that pass through the MgO
per second. At 1400°C, the diffusion coefficient of nickel ions in MgO is 9 * 10-12
cm2/s and the concentration of Ni on Ni/MgO surface equals 8.573 x 1022
atoms/cm3

5. ANSWER
• J =-D
𝑑𝑒𝑙𝑡𝑎 𝐶
𝐷𝑒𝑙𝑡𝑎 𝑥
•
𝑑𝑒𝑙𝑡𝑎 𝐶
𝐷𝑒𝑙𝑡𝑎 𝑥
=
0−8.573 𝑥 1022
0.05
= -1.715 * 1024 atoms/ cm3 .cm
• J= - (9 * 10-12 ) x( -1.715 * 1024 ) = 1.543*1013 𝑁𝑖 𝑎𝑡𝑜𝑚𝑠
𝑐𝑚2 𝑠
• Total Ni passing in one second = J
𝑁𝑖 𝑎𝑡𝑜𝑚𝑠
cm2 𝑠
x area (cm2) = 1.543*1013 x (2cm x
2cm)
• = 6.17 x 1013 Ni atoms/ s

6. SHEET 4
• Q7) An impermeable cylinder 3 cm in diameter and 10 cm long contains a gas
that includes 0.5 * 1020 N atoms per cm3 and 0.5 * 1020 H atoms per cm3 on one
side of an iron membrane . Gas is continuously introduced to the pipe to ensure a
constant concentration of nitrogen and hydrogen. The gas on the other side of
the membrane includes a constant 1 * 1018 N atoms per cm3 and 1 * 1018 H atoms
per cm3. The entire system is to operate at 700°C. Design an iron membrane
(BCC) that will

7. SHEET 4 – Q7
• allow no more than 1% of the nitrogen to be lost through the membrane each
hour
• allow 90% of the hydrogen to pass through the membrane per hour.
• Satisfy both later conditions
• given that for N D0 = 0.0047 cm2/s,, and E= 18300 cal/mol
• and for H D0 = 0.0012 cm2/s,, and E= 3600 cal/mol)

8. ANSWER

9. TO ALLOW NO MORE THAN 1% OF THE NITROGEN TO
BE LOST THROUGH THE MEMBRANE EACH HOUR
• The total number of nitrogen atoms in the container is
• 0.5 * 1020 x (pi/4) x 32 cm2 x 10 cm = 35.34 x 1020 N atom
• The maximum number of atoms to be lost = 1% from N per hour
• N atoms lost= 35.34 x 1020 N x 0.01 = 35.34 x 1018 N atoms per hour
J =
35.34 x 1018
3600 ∗32 ∗
pi
4
= 0.00139x 1018 N atoms per cm2 per
second

10. TO ALLOW NO MORE THAN 1% OF THE NITROGEN TO
BE LOST THROUGH THE MEMBRANE EACH HOUR
• Rate of diffusion (D) = c e-E/RT = 0.0047 x e-18300/1.98x973 =3.64x10-7
cm2/s
• dx=
−𝐷 ∗ 𝑑𝑐
𝐽
= −3.64 ∗ 10−7 ∗
1∗1018−0.5∗1020
0.00139 ∗1018 = 0.013 𝑐𝑚

11. ALLOW 90% OF THE HYDROGEN TO PASS
THROUGH THE MEMBRANE PER HOUR.
• H atom loss per hour = (0.90)(35.343 * 1020)= 31.80 * 1020
• J =
31.8 x 1020
3600 ∗32 ∗
pi
4
= 1.2 ∗ 1017 H atoms/ cm2 s
• D = 0.0012 e-3600/(1.98*973) = 1.86 x 10-4
• dx= ( -1.86* 10-4 * -49 * 1018 )/ 1.25 * 1017 = 0.073 cm

12. SATISFY BOTH LATER CONDITIONS
• An iron membrane with a thickness between 0.013 and 0.073 cm will be
satisfactory.