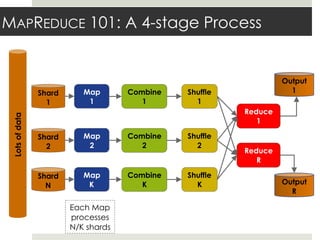
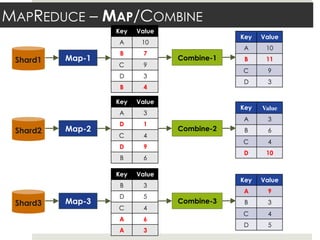
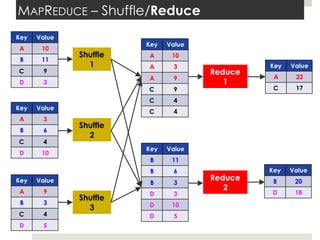
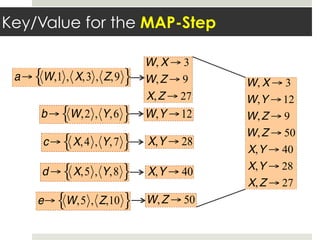
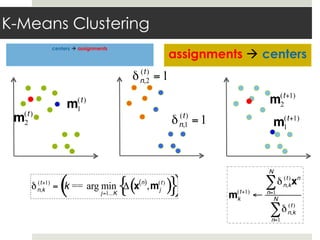
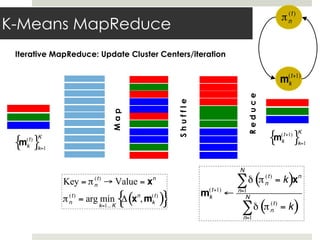
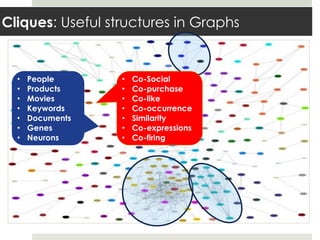
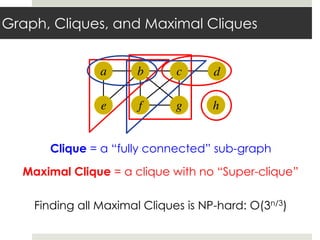
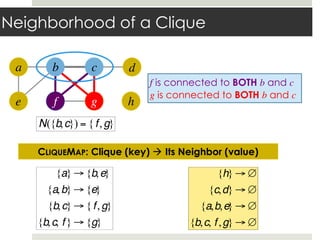
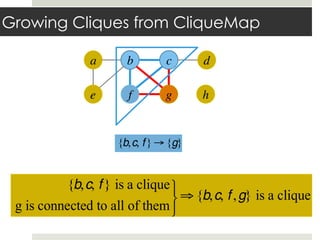
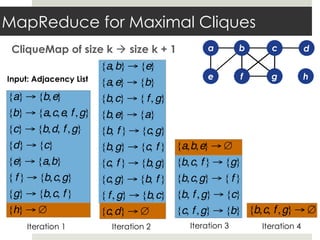
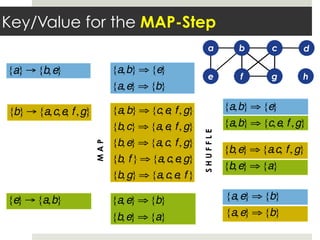
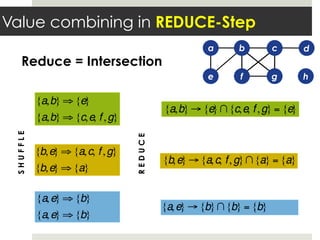
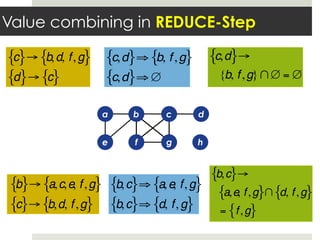
This document discusses parallelizing computation using MapReduce. It begins with an overview of MapReduce and how it works, breaking data into chunks that are processed in parallel by map tasks, and then combining results via reduce tasks. It then provides examples of using MapReduce to solve three problems: 1) calculating similarity between all pairs of documents, 2) parallelizing k-means clustering, and 3) finding all maximal cliques in a graph. For each problem it describes how to define the map and reduce functions to solve the problem in a data-parallel manner using MapReduce.

1. MapReduce and the
art of “Thinking Parallel”
Shailesh Kumar
Third Leap, Inc.

2. Three I’s of a great product!
Interface Intuitive |Functional | Elegant
Infrastructur
e
Storage |Computation |
Network
Intelligence Learn |Predict | Adapt |
Evolve

3. Drowning in Data, Starving for Knowledge
ATATTAGGTTTTTACCTACCC
AGGAAAAGCCAACCAACCTC
GATCTCTTGTAGATCTGTTCT
CTAAACGAACTTTAAAATCTG
TGTAGCTGTCGCTCGGCTG
CATGCCTAGTGCACCTACGC
AGTATAAACAATAATAAATTTT
ACTGTCGTTGACAAGAAACG
AGTAACTCGTCCCTCTTCTG
CAGACTGCTTATTACGCGAC
CGTAAGCTAC…

4. How BIG is Big Data?
600 million
tweets per DAY
100 hours per
MINUTE
800+ websites
per MINUTE
100 TB of data
uploaded DAILY
3.5 Billion
queries PER DAY
300 Million
Active customers
How BIG is BigData?

5. ▪ Better Sensors
▪ Higher resolution, Real-time, Diverse measurements, …
▪ Faster Communication
▪ Network infrastructure, Compression Technologies, …
▪ Cheaper Storage
▪ Cloud based storage, large warehouses, NoSQL databases
▪ Massive Computation
▪ Cloud computing, Mapreduce/Hadoop parallel processing paradigms
▪ Intelligent Decisions
▪ Advances in Machine Learning and Artificial Intelligence
How did we get here?

6. The Evolution of “Computing”

7. Parallel Computing Basics
▪ Data Parallelism (distributed computing)
▪ Lots of data ! Break it into “chunks”,
▪ Process each “chunk” of data in parallel,
▪ Combine results from each “chunk”
▪ MAPREDUCE = Data Parallelism
▪ Process Parallelism (data flow computing)
▪ Lots of stages ! Set up process graph
▪ Pass data through all stages
▪ All stages running in parallel on different data
▪ Assembly line = process parallelism

8. Agenda
MAPREDUCE Background
Problem 1 – Similarity between all pairs of documents!
Problem 2 – Parallelizing K-Means clustering
Problem 3 – Finding all Maximal Cliques in a Graph

9. MAPREDUCE 101: A 4-stage ProcessLotsofdata
Shard
1
Shard
N
Shard
2
Reduce
1
Reduce
R
Map
1
Map
2
Map
K
Combine
1
Combine
2
Combine
K
Shuffle
1
Shuffle
2
Shuffle
K
Output
1
Output
R
Each Map
processes
N/K shards

10. MAPREDUCE 101: An example Task
▪ Count total frequency of all words on the web
▪ Total number of documents > 20Billion
▪ Total number of unique words > 20Million
▪ Non-Parallel / Linear Implementation
for each document d on the Web
for each unique word w in d
DocCount w d( )= # times w occurred in d
WebCount w( ) += DocCount w d( )

11. MAPREDUCE – MAP/COMBINE
Shard1
Key Value
A 10
B 7
C 9
D 3
B 4
Key Value
A 10
B 11
C 9
D 3
Shard2
Key Value
A 3
D 1
C 4
D 9
B 6
Key Value
A 3
B 6
C 4
D 10
Shard3
Key Value
B 3
D 5
C 4
A 6
A 3
Map-1
Map-2
Map-3
Key Value
A 9
B 3
C 4
D 5
Combine-1
Combine-2
Combine-3

12. MAPREDUCE – Shuffle/Reduce
Key Value
A 10
B 11
C 9
D 3
Key Value
A 3
B 6
C 4
D 10
Key Value
A 9
B 3
C 4
D 5
Key Value
A 10
A 3
A 9
C 9
C 4
C 4
Key Value
B 11
B 6
B 3
D 3
D 10
D 5
Shuffle
1
Shuffle
2
Shuffle
3
Key Value
A 22
C 17
Key Value
B 20
D 18
Reduce
1
Reduce
2

13. Key Questions in MAPREDUCE
▪ Is the task really “data-parallelizable”?
▪ High dependence tasks (e.g. Fibonacci series)
▪ Recursive tasks (e.g. Binary Search)
▪ What is the key-value pair output for MAP step?
▪ Each map processes only one data record at a time
▪ It can generate none, one, or multiple key-value pairs
▪ How to combine values of a key in REDUCE step?
▪ The key for reduce is same as key for Map output
▪ The reduce function must be “order agnostic”

14. Other considerations
▪ Reliability/Robustness
▪ A processor or disk might go bad during the process
▪ Optimization/Efficiency
▪ Allocate CPU’s near data shards to reduce network overhead
▪ Scale/Parallelism
▪ Parallelization linearly proportional to number of machines
▪ Simplicity/Usability
▪ Just specify the Map task and the Reduce task and be done!
▪ Generality
▪ Lots of parallelizable tasks can be written in MapReduce
▪ With some creativity, many more than you can imagine!

15. Agenda
MAPREDUCE Background
Problem 1 – Similarity between all pairs of documents!
Problem 2 – Parallelizing K-Means clustering
Problem 3 – Finding all Maximal Cliques in a Graph

16. Similarity between all pairs of docs.
▪ Why bother?
▪ Document Clustering, Similar document search, etc.
▪ Document represented as a “Bag-of-Tokens”
▪ A weight associated with each tokens in vocabulary.
▪ Most weights are zero – Sparsity
▪ Cosine Similarity between two documents
di = w1
i
,w2
i
,...,wT
i
{ }, dj = w1
j
,w2
j
,...,wT
j
{ }
Sim di ,dj( )= wt
i
t=1
T
∑ × wt
j

17. Non-Parallel / Linear Implementation
For each document di
For each document dj ( j > i)
Sim di ,dj( )= wt
i
t=1
T
∑ × wt
j
Complexity = O D2
Tσ( )
σ = Sparsity factor =10−5
= Average Fraction of vocabulary per document
D = O(10B), T = O(10M )
Complexity = O 1020+7−5
( )= O 1022
( )

18. Toy Example for doc-doc similarity
A classic “Join”
Documents = W, X,Y, Z{ }, Words = a,b,c,d,e{ }
W → a,1 , b,2 , e,5{ }
X → a,3 , c,4 , d,5{ }
Y → b,6 , c,7 , d,8{ }
Z → a,9 , e,10{ }
Input W, X → Sim W, X( )= 3
W,Y → Sim W,Y( )= 12
W,Z → Sim W,Z( )= 59
X,Y → Sim X,Y( )= 68
X,Z → Sim X,Z( )= 27
Y,Z → Sim Y,Z( )= 0
Output

19. Reverse Indexing to the rescue
First convert the data to reverse index
a→ W,1 , X,3 , Z,9{ }
b→ W,2 , Y,6{ }
c→ X,4 , Y,7{ }
d → X,5 , Y,8{ }
e→ W,5 , Z,10{ }
W → a,1 , b,2 , e,5{ }
X → a,3 , c,4 , d,5{ }
Y → b,6 , c,7 , d,8{ }
Z → a,9 , e,10{ }

20. Key/Value for the MAP-Step
a→ W,1 , X,3 , Z,9{ }
W, X → 3
W,Z → 9
X,Z → 27
b→ W,2 , Y,6{ }
c→ X,4 , Y,7{ }
W,Y →12
e→ W,5 , Z,10{ }
d → X,5 , Y,8{ }
X,Y → 28
X,Y → 40
W,Z → 50
W, X → 3
W,Y →12
W,Z → 9
W,Z → 50
X,Y → 40
X,Y → 28
X,Z → 27

21. Value combining in REDUCE-Step
W, X → 3
W,Y →12
W,Z → 9
W,Z → 50
X,Y → 40
X,Y → 28
X,Z → 27
W, X → Sim W, X( )= 3
W,Y → Sim W,Y( )= 12
W,Z → Sim W,Z( )= 59
X,Y → Sim X,Y( )= 68
X,Z → Sim X,Z( )= 27
Y,Z → Sim Y,Z( )= 0

22. Agenda
MAPREDUCE Background
Problem 1 – Similarity between all pairs of documents!
Problem 2 – Parallelizing K-Means clustering
Problem 3 – Finding all Maximal Cliques in a Graph

23. assignments ! centers
K-Means Clustering
mk
(t+1)
←
δn,k
(t )
xn
n=1
N
∑
δn,k
(t)
n=1
N
∑
m1
(t+1)
m2
(t+1)
δn,2
(t )
= 1
δn,1
(t )
= 1
m1
(t )
m2
(t )
centers ! assignments
δn,k
(t+1)
= k == arg min
j=1...K
Δ x n( )
,mj
(t)
( ){ }( )

24. K-means clustering 101 – Non-parallel
E-Step – Update assignments from centers
M-Step – Update centers from cluster assignments
πn
(t)
← arg min
k=1...K
Δ xn
,mk
(t)
( ){ }
mk
(t+1)
←
δ πn
(t)
= k( )xn
n=1
N
∑
δ πn
(t)
= k( )
n=1
N
∑
O NKD( ):
N = Number of data points
K = Number of clusters
D = number of dimensions
⎧
⎨
⎪
⎩
⎪
O ND( ):
N = Number of data points
D = number of dimensions
⎧
⎨
⎩

25. K-Means MapReduce
mk
(t)
{ }k=1
K
Key = πn
(t)
→ Value = xn
πn
(t)
= arg min
k=1...K
Δ xn
,mk
(t)
( ){ } mk
(t+1)
←
δ πn
(t)
= k( )xn
n=1
N
∑
δ πn
(t)
= k( )
n=1
N
∑
mk
(t+1)
{ }k=1
K
πn
(t)
mk
(t+1)
Map
Shuffle
Reduce
Iterative MapReduce: Update Cluster Centers/iteration

26. Agenda
MAPREDUCE Background
Problem 1 – Similarity between all pairs of documents!
Problem 2 – Parallelizing K-Means clustering
Problem 3 – Finding all Maximal Cliques in a Graph

27. Cliques: Useful structures in Graphs
• People
• Products
• Movies
• Keywords
• Documents
• Genes
• Neurons
• Co-Social
• Co-purchase
• Co-like
• Co-occurrence
• Similarity
• Co-expressions
• Co-firing

28. guitarist
rock-music
guitar
song
musician
rock-band
singer
electric-guitar
singing
university
school
college
student
classroom
school-teacher
teacher
teacher-student-relationship
judge
lawsuit
trial
lawyerfalse-persecution
perjury
courtroom
Example Concepts in IMDB

29. Graph, Cliques, and Maximal Cliques
Clique = a “fully connected” sub-graph
Maximal Clique = a clique with no “Super-clique”
Finding all Maximal Cliques is NP-hard: O(3n/3)
a
e
b
f
c
g
d
h

30. Neighborhood of a Clique
a
e
b
f
c
g
d
h
f is connected to BOTH b and c
g is connected to BOTH b and c
N({b,c}) = {f,g}
CLIQUEMAP: Clique (key) ! Its Neighbor (value)
{a} → {b,e}
{a,b} → {e}
{b,c} → { f,g}
{b,c, f } → {g}
{h} → ∅
{c,d} → ∅
{a,b,e} → ∅
{b,c, f ,g} → ∅

31. Growing Cliques from CliqueMap
{b,c, f} → {g}
a
e
b
f
c
g
d
h
{b,c, f} is a clique
g is connected to all of them
⎫
⎬
⎭
⇒ {b,c, f,g} is a clique

32. MapReduce for Maximal Cliques
CliqueMap of size k ! size k + 1
{a,b} → {e}
{a,e} → {b}
{b,c} → { f,g}
{b,e} → {a}
{b, f } → {c,g}
{b,g} → {c, f }
{c, f } → {b,g}
{c, g} → {b, f }
{ f, g} → {b,c}
{c,d} → ∅
Iteration 2
{a,b,e} → ∅
{b,c, f } → {g}
{b,c,g} → { f }
{b, f ,g} → {c}
{c, f ,g} → {b}
Iteration 3
{b,c, f,g} → ∅
Iteration 4
{a} → {b,e}
{b} → {a,c,e, f ,g}
{c} → {b,d, f ,g}
{d} → {c}
{e} → {a,b}
{ f } → {b,c,g}
{g} → {b,c, f }
{h} → ∅
Iteration 1
Input: Adjacency List
a
e
b
f
c
g
d
h

33. Key/Value for the MAP-Step
a
e
b
f
c
g
d
h
{a} → {b,e} {a,b} ⇒ {e}
{a,e} ⇒ {b}
{e} → {a,b}
{b} → {a,c,e, f,g}
{a,e} ⇒ {b}
{b,e} ⇒ {a}
{a,b} ⇒ {c,e, f, g}
{b,c} ⇒ {a,e, f, g}
{b,e} ⇒ {a,c, f, g}
{b, f } ⇒ {a,c,e, g}
{b,g} ⇒ {a,c,e, f }
{a,e} ⇒ {b}
{a,e} ⇒ {b}
{a,b} ⇒ {e}
{a,b} ⇒ {c,e, f ,g}
{b,e} ⇒ {a.c, f,g}
{b,e} ⇒ {a}
SHUFFLE
MAP

34. Value combining in REDUCE-Step
a
e
b
f
c
g
d
h
{a,e} ⇒ {b}
{a,e} ⇒ {b}
{a,b} ⇒ {e}
{a,b} ⇒ {c,e, f ,g}
{b,e} ⇒ {a,c, f ,g}
{b,e} ⇒ {a}
SHUFFLE
{a,b} → {e}∩{c,e, f,g} = {e}
{b,e} → {a,c, f,g}∩{a} = {a}
{a,e} → {b}∩{b} = {b}
REDUCE
Reduce = Intersection

35. Value combining in REDUCE-Step
a
e
b
f
c
g
d
h
c,d{ }⇒ b, f ,g{ }
c,d{ }⇒ ∅
c{ }→ b,d, f,g{ }
d{ }→ c{ }
b,c{ }⇒ a,e, f,g{ }
b,c{ }⇒ d, f,g{ }
b{ }→ a,c,e, f,g{ }
c{ }→ b,d, f ,g{ }
c,d{ }→
{b, f ,g}∩∅ = ∅
b,c{ }→
a,e, f ,g{ }∩ d, f ,g{ }
= f ,g{ }

36. “Art of Thinking Parallel” is about
▪ Transforming the Input Data appropriately
▪ e.g. Reverse Indexing (doc-doc similarity)
▪ Breaking the problem into smaller ones
▪ e.g. Iterative MapReduce (clustering)
▪ Designing the Map step - Key/Value output
▪ e.g. CliqueMaps in Maximal Cliques
▪ Design the Reduce step – Combine values of key
▪ e.g. Intersections in Maximal Cliques