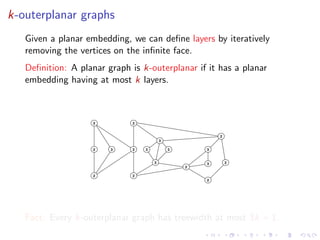
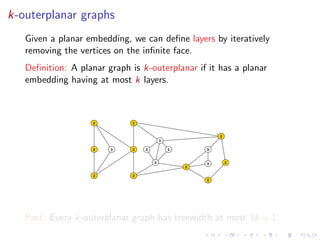
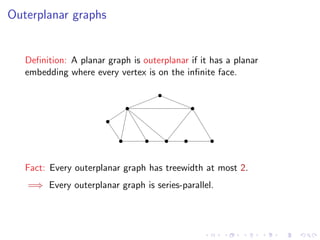
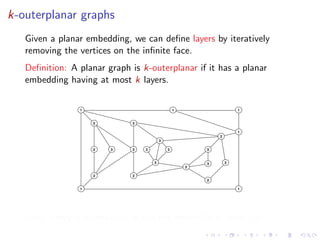
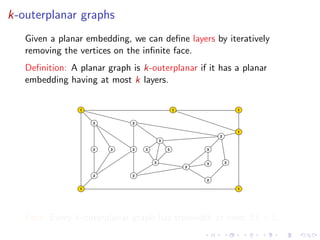
The document discusses applications of graphs with bounded treewidth. It covers the following key points: 1) Courcelle's theorem shows that many NP-complete graph problems can be solved in linear time for graphs of bounded treewidth using monadic second-order logic. This includes problems like independent set, coloring, and Hamiltonian cycle. 2) The treewidth of a graph is closely related to its largest grid minor - graphs with large treewidth contain large grid minors. There are polynomial relationships between treewidth and largest grid minor for planar graphs. 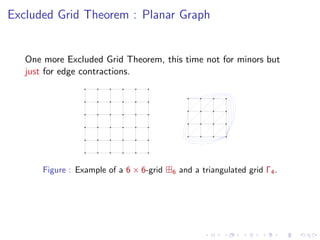3) Planar graphs have bounded treewidth if and only if they exclude some grid configuration as a contraction. This helps characterize planar graphs of bounded treewidth

1. Treewidth 2: Applications
Saket Saurabh
The Institute of Mathematical Sciences, India
ASPAK 2014, March 3-8

2. Introduction and definition DONE
Part I: Algorithms for bounded treewidth graphs. DONE
Part II: Graph-theoretic properties of treewidth.
Part III: Applications for general graphs.
Part IV: Algorithm for finding treewidth
Part V: Irrelevant Vertices – Planar Vertex Deletion.

3. Applications
Algorithms for graphs of bounded treewidth find many
applications, for example in
Graph Minors
Exact Algorithms
Approximation Schemes
Parameterized Algorithms
Kernelization
Databases
CSP’s

4. Application I: Parameterized Algorithms
Extended Monadic Second Order Logic (EMSO) A logical language
on graphs consisting of the following:
Logical connectives ∧, ∨, →, ¬, =, =
quantifiers ∀, ∃ over vertex/edge variables
predicate adj(u, v ): vertices u and v are adjacent
predicate inc(e, v ): edge e is incident to vertex v
∈, ⊆ for vertex/edge sets
Example: The formula
∃C ⊆ V ∀v ∈ C ∃u1 , u2 ∈ C (u1 = u2 ∧ adj(u1 , v ) ∧ adj(u2 , v )) is
true . . .if graph G (V , E ) has a cycle.

5. Application I: Parameterized Algorithms
Extended Monadic Second Order Logic (EMSO) A logical language
on graphs consisting of the following:
Logical connectives ∧, ∨, →, ¬, =, =
quantifiers ∀, ∃ over vertex/edge variables
predicate adj(u, v ): vertices u and v are adjacent
predicate inc(e, v ): edge e is incident to vertex v
∈, ⊆ for vertex/edge sets
Example: The formula
∃C ⊆ V ∀v ∈ C ∃u1 , u2 ∈ C (u1 = u2 ∧ adj(u1 , v ) ∧ adj(u2 , v )) is
true . . .if graph G (V , E ) has a cycle.

6. Application I: Parameterized Algorithms
Extended Monadic Second Order Logic (EMSO) A logical language
on graphs consisting of the following:
Logical connectives ∧, ∨, →, ¬, =, =
quantifiers ∀, ∃ over vertex/edge variables
predicate adj(u, v ): vertices u and v are adjacent
predicate inc(e, v ): edge e is incident to vertex v
∈, ⊆ for vertex/edge sets
Example: The formula
∃C ⊆ V ∀v ∈ C ∃u1 , u2 ∈ C (u1 = u2 ∧ adj(u1 , v ) ∧ adj(u2 , v )) is
true . . .if graph G (V , E ) has a cycle.

7. Courcelle’s Theorem
Courcelle’s Theorem: If a graph property can be expressed in
EMSO with formula ϕ of size |ϕ|, then for every fixed w ≥ 1, there
is an algorithm running in time f (|ϕ|, w ) · n for testing this
property on graphs having treewidth at most w .
Independent Set, Dominating Set, q Coloring, Max Cut, Odd Cycle
Transversal, Hamiltonian Cycle, Partition into Triangles, Feedback
Vertex Set, Vertex Disjoint Cycle Packing and million other
problems are FPT parameterized by the treewidth.

8. Courcelle’s Theorem
Courcelle’s Theorem: If a graph property can be expressed in
EMSO with formula ϕ of size |ϕ|, then for every fixed w ≥ 1, there
is an algorithm running in time f (|ϕ|, w ) · n for testing this
property on graphs having treewidth at most w .
Independent Set, Dominating Set, q Coloring, Max Cut, Odd Cycle
Transversal, Hamiltonian Cycle, Partition into Triangles, Feedback
Vertex Set, Vertex Disjoint Cycle Packing and million other
problems are FPT parameterized by the treewidth.

9. Properties of treewidth
Fact: treewidth ≤ 2 if and only if graph
is subgraph of a series-parallel graph

10. Properties of treewidth
Fact: treewidth ≤ 2 if and only if graph
is subgraph of a series-parallel graph
Fact: For every k ≥ 2, the treewidth of
the k × k grid is exactly k.

11. Properties of treewidth
Fact: treewidth ≤ 2 if and only if graph
is subgraph of a series-parallel graph
Fact: For every k ≥ 2, the treewidth of
the k × k grid is exactly k.
Fact: Treewidth does not increase if we delete edges, delete
vertices, or contract edges.
=⇒ If F is a minor of G , then the treewidth of F is at most the
treewidth of G .

12. Properties of treewidth
Fact: treewidth ≤ 2 if and only if graph
is subgraph of a series-parallel graph
Fact: For every k ≥ 2, the treewidth of
the k × k grid is exactly k.
Fact: Treewidth does not increase if we delete edges, delete
vertices, or contract edges.
=⇒ If F is a minor of G , then the treewidth of F is at most the
treewidth of G .
The treewidth of the k-clique is k − 1.

13. Obstruction to Treewidth
Figure : Example of a 6 × 6-grid
6
and a triangulated grid Γ4 .
Another, extremely useful obstructions to small treewidth, are
grid-minors. Let t be a positive integer. The t × t-grid t is a
graph with vertex set {(x, y ) | x, y ∈ {1, 2, . . . , t}}. Thus t has
exactly t 2 vertices. Two different vertices (x, y ) and (x , y ) are
adjacent if and only if |x − x | + |y − y | ≤ 1. The border of t is
the set of vertices with coordinates (1, y ), (t, y ), (t, 1), and (x, t),
where x, y ∈ {1, 2, . . . , t}

14. As we already have seen, if a graph contains large grid as a minor,
its treewidth is also large.

15. As we already have seen, if a graph contains large grid as a minor,
its treewidth is also large.
What is much more surprising, is that the converse is also true,
every graph of large treewidth contains a large grid as a minor.

16. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]

17. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]
It was open for many years whether a polynomial relationship could
be established between the treewidth of a graph G and the size of
its largest grid minor.

18. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]
It was open for many years whether a polynomial relationship could
be established between the treewidth of a graph G and the size of
its largest grid minor.
Theorem (Excluded Grid Theorem, Chekuri and Chuzhoy)
Let t ≥ 0 be an integer. There exists a universal constant c, such
that every graph of treewidth at least c · t 99 contains t as a
minor.

19. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]

20. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]
It was open for many years whether a polynomial relationship could
be established between the treewidth of a graph G and the size of
its largest grid minor.

21. Excluded Grid Theorem
Fact: [Excluded Grid Theorem] If the treewidth of G is at least
2
k 4k (k+2) , then G has a k × k grid minor.
[Robertson and Seymour ]
It was open for many years whether a polynomial relationship could
be established between the treewidth of a graph G and the size of
its largest grid minor.
Theorem (Excluded Grid Theorem, Chekuri and Chuzhoy)
Let t ≥ 0 be an integer. There exists a universal constant c, such
that every graph of treewidth at least c · t 99 contains t as a
minor.

22. Excluded Grid Theorem A : Planar Graph
Much better relations. We have two theorems:
Theorem (Planar Excluded Grid Theorem)
Let t ≥ 0 be an integer. Every planar graph G of treewidth at
least 9 t, contains t as a minor. Furthermore, there exists a
2
polynomial-time algorithm that for a given planar graph G either
outputs a tree decomposition of G of width 9 t or constructs a
2
minor model of t in G .

23. Excluded Grid Theorem : Planar Graph
One more Excluded Grid Theorem, this time not for minors but
just for edge contractions.
Figure : Example of a 6 × 6-grid
6
and a triangulated grid Γ4 .

24. Excluded Grid Theorem : Planar Graph
One more Excluded Grid Theorem, this time not for minors but
just for edge contractions.
Figure : Example of a 6 × 6-grid
6
and a triangulated grid Γ4 .
For an integer t > 0 the graph Γt is obtained from the grid t by
adding for every 1 ≤ x, y ≤ t − 1, the edge (x, y ), (x + 1, y + 1),
and making the vertex (t, t) adjacent to all vertices with x ∈ {1, t}
and y ∈ {1, t}.

25. Excluded Grid Theorem : Planar Graph
Figure : Example of a 6 × 6-grid
6
and a triangulated grid Γ4 .
Theorem
For any connected planar graph G and integer t ≥ 0, if
tw(G ) ≥ 9(t + 1), then G contains Γt as a contraction.
Furthermore there exists a polynomial-time algorithm that given G
either outputs a tree decomposition of G of width 9(t + 1) or a set
of edges whose contraction result in Γt .

26. Excluded Grid Theorem : Planar Graph
One more Excluded Grid Theorem, this time not for minors but
just for edge contractions.
Theorem
For any connected planar graph G and integer t ≥ 0, if
tw(G ) ≥ 9(t + 1), then G contains Γt as a contraction.
Furthermore there exists a polynomial-time algorithm that given G
either outputs a tree decomposition of G of width 9(t + 1) or a set
of edges whose contraction result in Γt .

27. Excluded Grid Theorem : Planar Graph
One more Excluded Grid Theorem, this time not for minors but
just for edge contractions.
Theorem
For any connected planar graph G and integer t ≥ 0, if
tw(G ) ≥ 9(t + 1), then G contains Γt as a contraction.
Furthermore there exists a polynomial-time algorithm that given G
either outputs a tree decomposition of G of width 9(t + 1) or a set
of edges whose contraction result in Γt .
Can we have such theorems for general
graphs?

28. Outerplanar graphs
Definition: A planar graph is outerplanar if it has a planar
embedding where every vertex is on the infinite face.

29. Outerplanar graphs
Definition: A planar graph is outerplanar if it has a planar
embedding where every vertex is on the infinite face.
Fact: Every outerplanar graph has treewidth at most 2.
=⇒ Every outerplanar graph is series-parallel.

30. k-outerplanar graphs
Given a planar embedding, we can define layers by iteratively
removing the vertices on the infinite face.
Definition: A planar graph is k-outerplanar if it has a planar
embedding having at most k layers.
1
1
2
1
2
1
2
3
2
3
2
3
3
3
3
3
2
2
2
2
2
1
1
Fact: Every k-outerplanar graph has treewidth at most 3k + 1.

31. k-outerplanar graphs
Given a planar embedding, we can define layers by iteratively
removing the vertices on the infinite face.
Definition: A planar graph is k-outerplanar if it has a planar
embedding having at most k layers.
1
1
2
1
2
1
2
3
2
3
2
3
3
3
3
3
2
2
2
2
2
1
1
Fact: Every k-outerplanar graph has treewidth at most 3k + 1.

32. k-outerplanar graphs
Given a planar embedding, we can define layers by iteratively
removing the vertices on the infinite face.
Definition: A planar graph is k-outerplanar if it has a planar
embedding having at most k layers.
2
2
2
3
2
3
2
3
3
3
3
3
2
2
2
2
2
Fact: Every k-outerplanar graph has treewidth at most 3k + 1.

33. k-outerplanar graphs
Given a planar embedding, we can define layers by iteratively
removing the vertices on the infinite face.
Definition: A planar graph is k-outerplanar if it has a planar
embedding having at most k layers.
2
2
2
3
2
3
2
3
3
3
3
3
2
2
2
2
2
Fact: Every k-outerplanar graph has treewidth at most 3k + 1.

34. k-outerplanar graphs
Given a planar embedding, we can define layers by iteratively
removing the vertices on the infinite face.
Definition: A planar graph is k-outerplanar if it has a planar
embedding having at most k layers.
3
3
3
3
3
3
3
Fact: Every k-outerplanar graph has treewidth at most 3k + 1.

35. Shifting Techniques

36. Building Blocks of the Technique
r
For vertex v of a graph G and integer r ≥ 1, we denote by Gv the
subgraph of G induced by vertices within distance r from v in G .

37. Building Blocks of the Technique
r
For vertex v of a graph G and integer r ≥ 1, we denote by Gv the
subgraph of G induced by vertices within distance r from v in G .
Lemma
Let G be a planar graph, v ∈ V (G ) and r ≥ 1. Then
r
tw(Gv ) ≤ 18(r + 1).
Proof.
On board.

38. Building Blocks of the Technique
r
For vertex v of a graph G and integer r ≥ 1, we denote by Gv the
subgraph of G induced by vertices within distance r from v in G .
Lemma
Let G be a planar graph, v ∈ V (G ) and r ≥ 1. Then
r
tw(Gv ) ≤ 18(r + 1).
Proof.
On board.
18(r + 1) in the above proof can be made 3r + 1.
Lemma
Let v be a vertex of a planar graph G and let Li , be the vertices of
G at distance i, 0 ≤ i ≤ n, from v . Then for any i, j ≥ 0, the
treewidth of the subgraph Gi,i+j induced by vertices in
Li ∪ Li+1 ∪ · · · ∪ Li+ j does not exceed 3j + 1.
Proof.
On board.

39. Intuition
The idea behind the shifting technique is as follows.
Pick a vertex v of planar graph G and run breadth-first search
(BFS) from v .
For any i, j ≥ 0, the treewidth of the subgraph Gi,i+j induced
by vertices in levels i, i + 1, . . . , i + j of BFS does not exceed
3j + 1.
Now for an appropriate choice of parameters, we can find
a“shift” of “windows”, i.e. a disjoint set of a small number of
consecutive levels of BFS, “covering” the solution. Because
every window is of small treewidth, we can employ the
dynamic programing or the power of Courcelle’s theorem to
solve the problem.
We will see two examples.

40. Intuition
The idea behind the shifting technique is as follows.
Pick a vertex v of planar graph G and run breadth-first search
(BFS) from v .
For any i, j ≥ 0, the treewidth of the subgraph Gi,i+j induced
by vertices in levels i, i + 1, . . . , i + j of BFS does not exceed
3j + 1.
Now for an appropriate choice of parameters, we can find
a“shift” of “windows”, i.e. a disjoint set of a small number of
consecutive levels of BFS, “covering” the solution. Because
every window is of small treewidth, we can employ the
dynamic programing or the power of Courcelle’s theorem to
solve the problem.
We will see two examples.

41. Intuition
The idea behind the shifting technique is as follows.
Pick a vertex v of planar graph G and run breadth-first search
(BFS) from v .
For any i, j ≥ 0, the treewidth of the subgraph Gi,i+j induced
by vertices in levels i, i + 1, . . . , i + j of BFS does not exceed
3j + 1.
Now for an appropriate choice of parameters, we can find
a“shift” of “windows”, i.e. a disjoint set of a small number of
consecutive levels of BFS, “covering” the solution. Because
every window is of small treewidth, we can employ the
dynamic programing or the power of Courcelle’s theorem to
solve the problem.
We will see two examples.

42. Intuition
The idea behind the shifting technique is as follows.
Pick a vertex v of planar graph G and run breadth-first search
(BFS) from v .
For any i, j ≥ 0, the treewidth of the subgraph Gi,i+j induced
by vertices in levels i, i + 1, . . . , i + j of BFS does not exceed
3j + 1.
Now for an appropriate choice of parameters, we can find
a“shift” of “windows”, i.e. a disjoint set of a small number of
consecutive levels of BFS, “covering” the solution. Because
every window is of small treewidth, we can employ the
dynamic programing or the power of Courcelle’s theorem to
solve the problem.
We will see two examples.

43. Subgraph Isomorphism
Subgraph Isomorphism: given graphs H and G , find a copy of
H in G as subgraph. Parameter k := |V (H)|.
EMSO formula of size k O(1) for Subgraph Isomorphism exists.
This now using Courcelle’s Theorem implies that we have
f (k, w ) · n time algorithm for Subgraph Isomorphism on
graphs of treewidth w .

44. Subgraph Isomorphism
Subgraph Isomorphism: given graphs H and G , find a copy of
H in G as subgraph. Parameter k := |V (H)|.
EMSO formula of size k O(1) for Subgraph Isomorphism exists.
This now using Courcelle’s Theorem implies that we have
f (k, w ) · n time algorithm for Subgraph Isomorphism on
graphs of treewidth w .

45. Subgraph Isomorphism
Subgraph Isomorphism: given graphs H and G , find a copy of
H in G as subgraph. Parameter k := |V (H)|.
EMSO formula of size k O(1) for Subgraph Isomorphism exists.
This now using Courcelle’s Theorem implies that we have
f (k, w ) · n time algorithm for Subgraph Isomorphism on
graphs of treewidth w .

46. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

47. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

48. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

49. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

50. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

51. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

52. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

53. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

54. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

55. Baker’s shifting strategy
Subgraph Isomorphism for planar graphs: given planar graphs H and
G , find a copy of H in G as subgraph. Parameter k := |V (H)|.
Layers of the planar
graph:
(as in the definition of
k-outerplanar):
For a fixed 0 ≤ s < k + 1, delete every layer Li with i = s
(mod k + 1)
The resulting graph is k-outerplanar, hence it has treewidth at most
3k + 1.
Using the f (k, w ) · n time algorithm for Subgraph Isomorphism,
the problem can be solved in time f (k, 3k + 1) · n.
We do this for every 0 ≤ s < k + 1: for at least one value of s, we
do not delete any of the k vertices of the solution =⇒ we find a
copy of H in G if there is one.
Subgraph Isomorphism for planar graphs is FPT parameterized
by k := |V (H)|.

56. Bisection
For a given n-vertex graph G , weight function w : V (G ) → N and
integer k, the task is to decide if there is a partition of V (G ) into
sets V1 and V2 of weights w (V (G ))/2 and w (V (G )/2 and
such that the number of edges between V1 and V2 is at most k. In
other words, we are looking for a balanced partition (V1 , V2 ) with
a (V1 , V2 )-cut at most k.

57. Bisection
For a given n-vertex graph G , weight function w : V (G ) → N and
integer k, the task is to decide if there is a partition of V (G ) into
sets V1 and V2 of weights w (V (G ))/2 and w (V (G )/2 and
such that the number of edges between V1 and V2 is at most k. In
other words, we are looking for a balanced partition (V1 , V2 ) with
a (V1 , V2 )-cut at most k.
Lemma
Bisection is solvable in time 2t · nO(1) on an n-vertex given
together with its tree decomposition of width t.
Theorem
Bisection on planar graphs is solvable in time 2O(k) · nO(1) .
Proof.
On board.

58. Approximation schemes
Definition: A polynomial-time approximation scheme (PTAS) for a
problem P is an algorithm that takes an instance of P and a
rational number ε > 0,
always finds a (1 + ε)-approximate solution,
the running time is polynomial in n for every fixed ε > 0.
2
Typical running times: 21/ε · n, n1/ε , (n/ε)2 , n1/ε .
Some classical problems that have a PTAS:
Independent Set for planar graphs
TSP in the Euclidean plane
Steiner Tree in planar graphs
Knapsack

59. Baker’s shifting strategy for EPTAS
Fact: There is a 2O(1/ε) · n time PTAS for Independent Set for
planar graphs.
Let D := 1/ε. For a fixed 0 ≤ s < D, delete every layer Li
with i = s (mod D)
The resulting graph is D-outerplanar, hence it has treewidth
at most 3D + 1 = O(1/ε).
Using the O(2w · n) time algorithm for Independent Set,
the problem can be solved in time 2O(1/ε) · n.
We do this for every 0 ≤ s < D: for at least one value of s,
we delete at most 1/D = ε fraction of the solution =⇒ we
get a (1 − ε)-approximate solution.

60. Bidimensionality