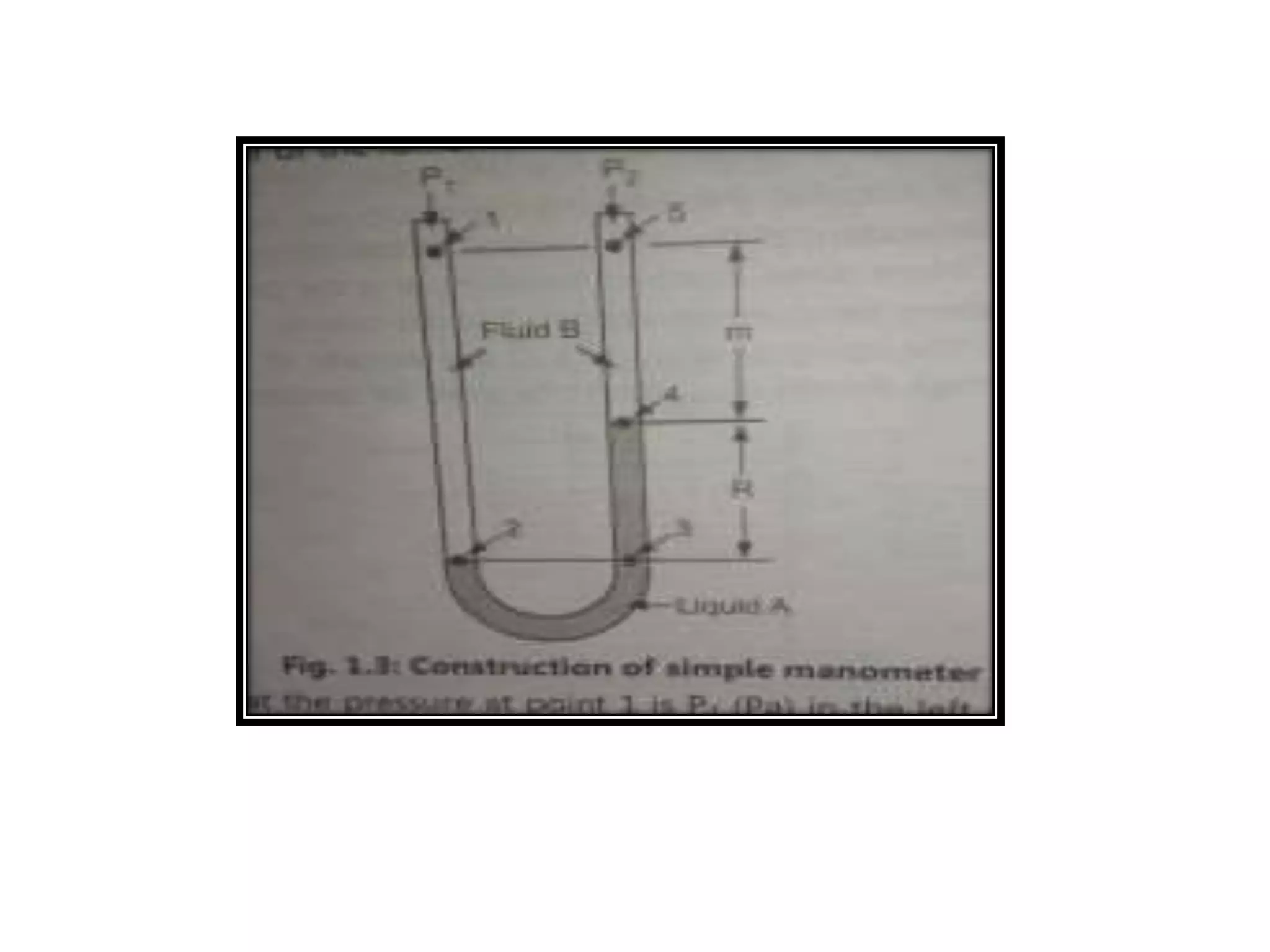
Manometers are devices used to measure pressure differences. There are three main types: simple manometers, differential manometers, and inclined tube manometers. A simple manometer uses a U-shaped tube filled with two immiscible liquids of different densities. By measuring the difference in liquid levels, the pressure difference between the two arms of the tube can be determined. This pressure difference depends on the density difference of the liquids and gravitational acceleration. Inclined manometers modify the simple design by inclining one limb of the tube, amplifying small pressure readings and making them easier to measure.

1. Manometer are device used to measure the pressure difference values.
Types of Manometer
1.Simple Manometer
2.Differential Manometer
3.Inclined tube manometer
Manometer

3. A simple manometer is a tube gauge for measuring high as well as
negative pressures.
It is the simplest form, having a U shaped bent tube, one end of
which is attached to the gauge point and the other end is open to
the atmosphere.
The construction of a simple manometer is shown in Fig.
The U shaped glass tube is filled with a liquid (A) of density,
ρA, kg/m3.
Above liquid A, the tube arms are filled with a lighter liquid B of
density ρB, kg/m.

4. Both the liquids are immiscible and the junction interface is clearly
visible. Generally, liquid A is mercury which is 13.6 times denser
than water and therefore, suitable for measuring high pressures also.
When two different pressures are applied to the arms of manometer,
the liquid A shows a movement so that the meniscus in both the arms
is at different levels. Consider various This manom
points (1 to 5) in the center of the lumen of U tube at different
distances as shown in Fig. 1.3.

5. Let us suppose that the pressure at point 1 is P1 (Pa) in the left arm of the figure and
at point 5 is P2 (Pa) in the right arm of the figure. pressure at
point 2 can be written as:
pressure at point 2 = P1+h.ρ.g................................1
Here h is height of liquid above the point 2 i.e. (m+R)and density is .gB
So
Pressure at point 2= P1+(m+R).ρB.g.......................................2
Pressure at points 2 and 3 are at same level,pressure at point 3 is
Pressure at point 3= Pressure at points 2=P1 +(m+R).ρB.g............3
Now pressure at point 4 in terms of P2 can be written
Pressure at point 4= P2+m.ρB.g.......................................4

6. In another form, the pressure at point 4 can also be written in terms of
P1 from the left
arm as:
Pressure at point 4 = P1+(m+R).ρB.g - RρA.g.............5
Since both the points are same, both these equations 4 and 5 should be
equal,
Hence, the pressure at point 4 can be re-written as:
P1 +(m + R). ρB.g-R. ρA.g = P2 + m. ρB.g
P1- P2 = m. ρB.g - (m + R). ρB.g + R. ρA.g
∆P = m. ρB.g -m ρB.g -R ρB.g + R. ρA.g
∆P =R.(ρA- ρB ).g
Thus the value of ∆P is independent of the distance m and dimension of
U tube with a condition that P1 and P2 are measured in the same
horizontal plane

7. Inclined Manometer
It is a kind of modified simple manometer used to measure
small difference in pressure.
In this type, one limb of the manometer is inclined in such
a way that for a very small value of actual reading R, the
meniscus moves a considerable distance (inclined reading)
so that it can be noted easily. The inclined distance is equal
to the actual reading R divided by the sine of angle of
inclination α (sin α). Thus by making α small, the value of
inclined reading R, can be increased.
∆P = P1- P2 = Ri(ρa - ρ B).g
∆ P = P1- P2 = (R/sin α) (ρa - ρ B).g