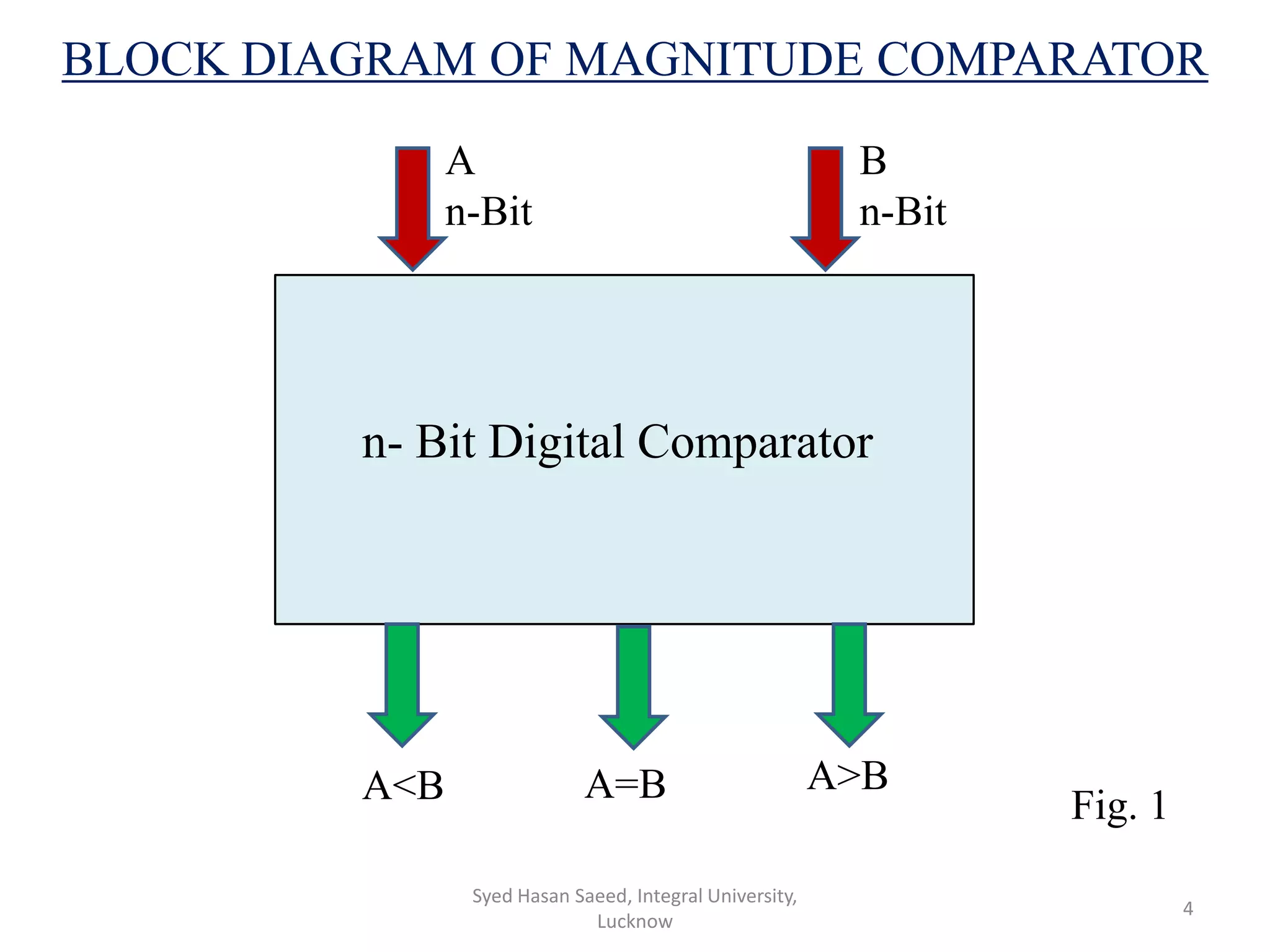
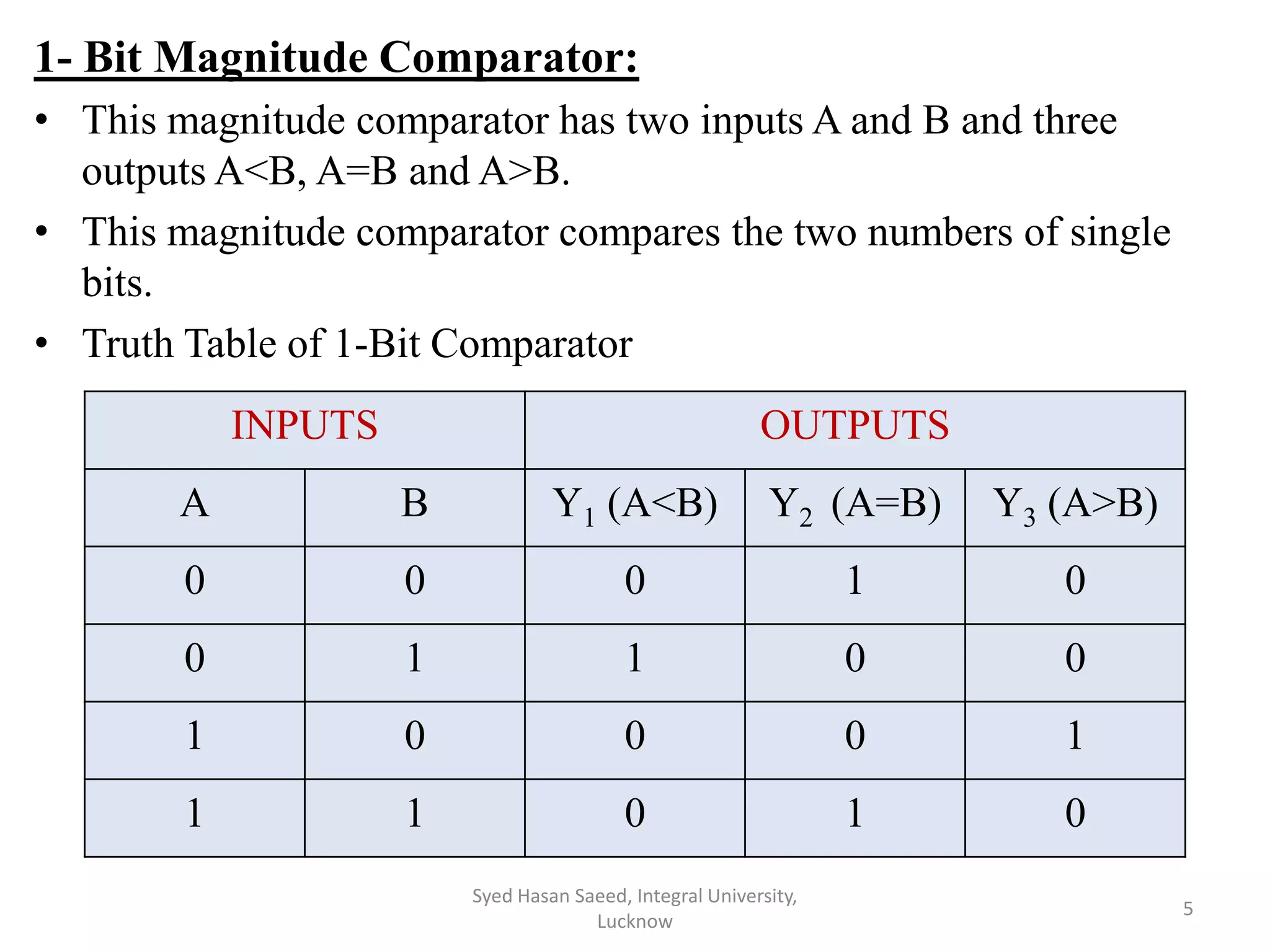
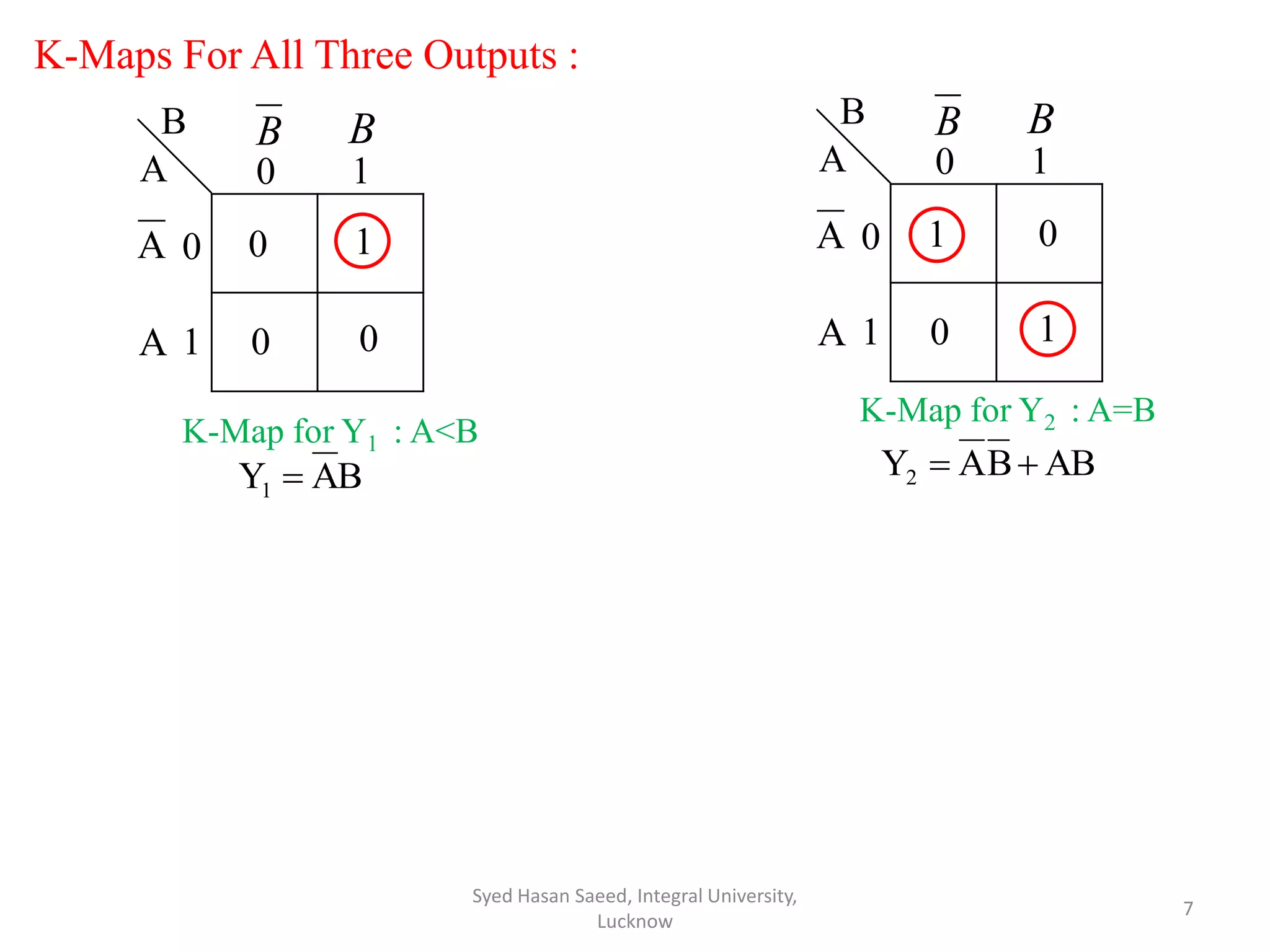
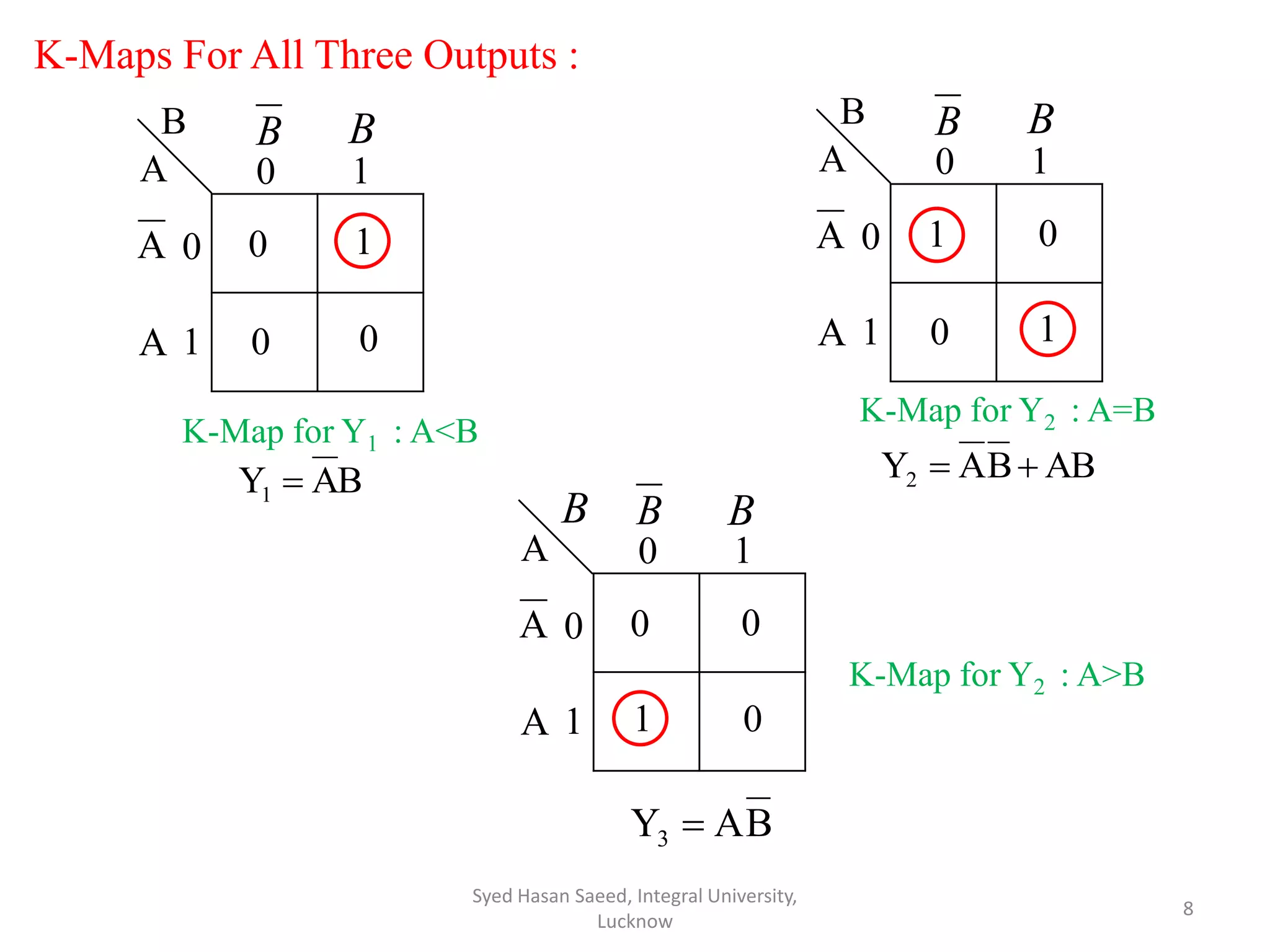
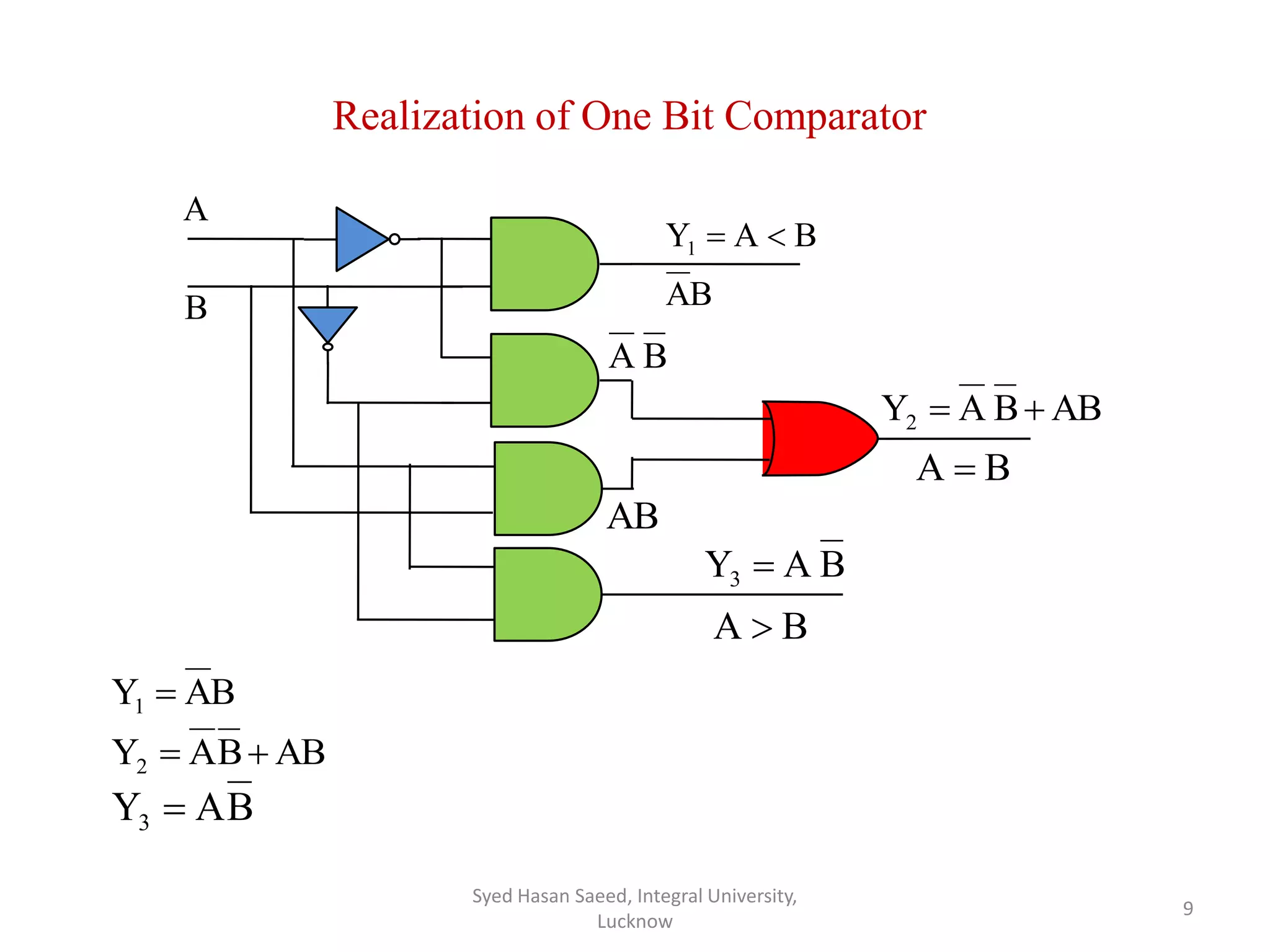
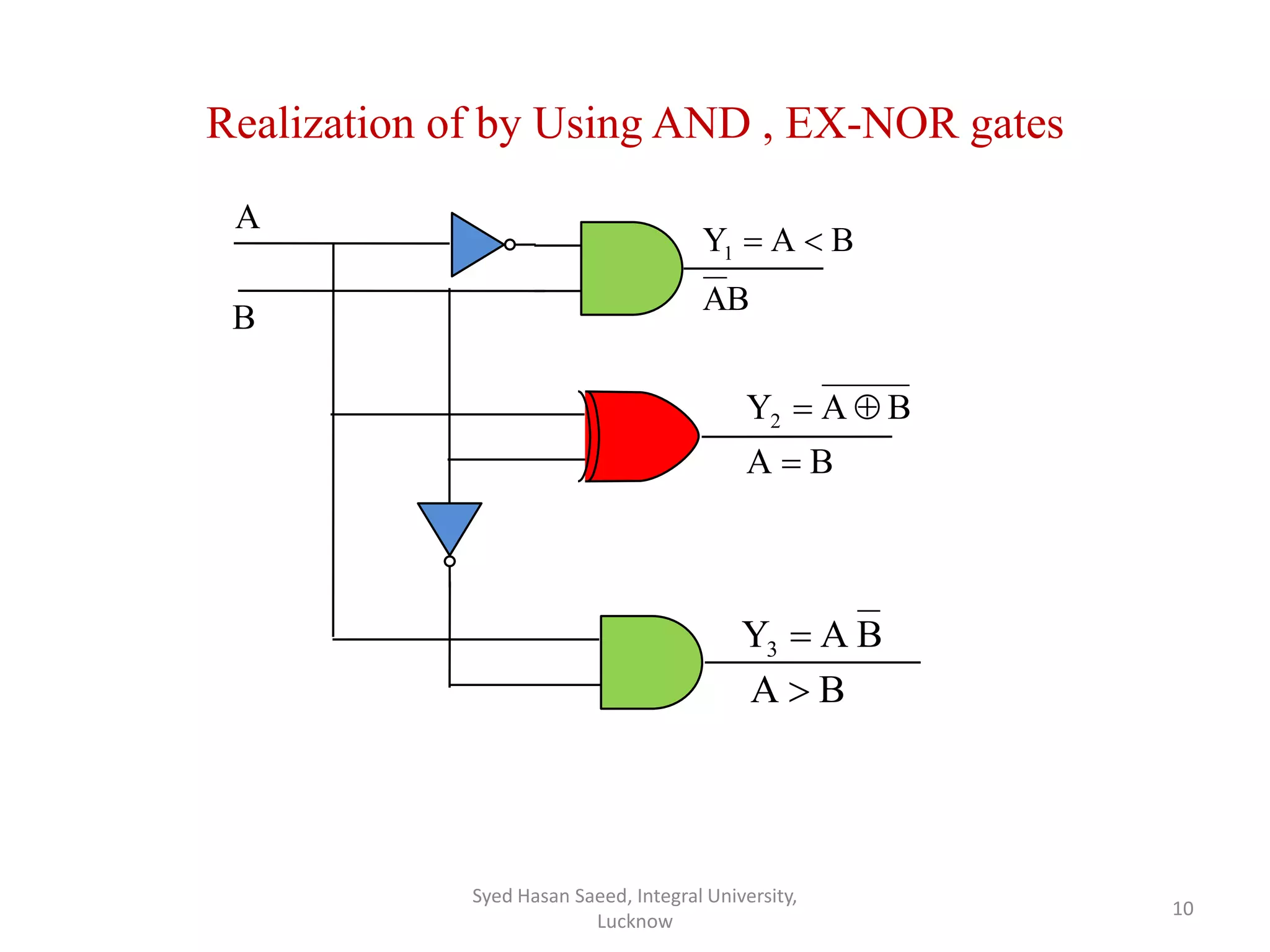
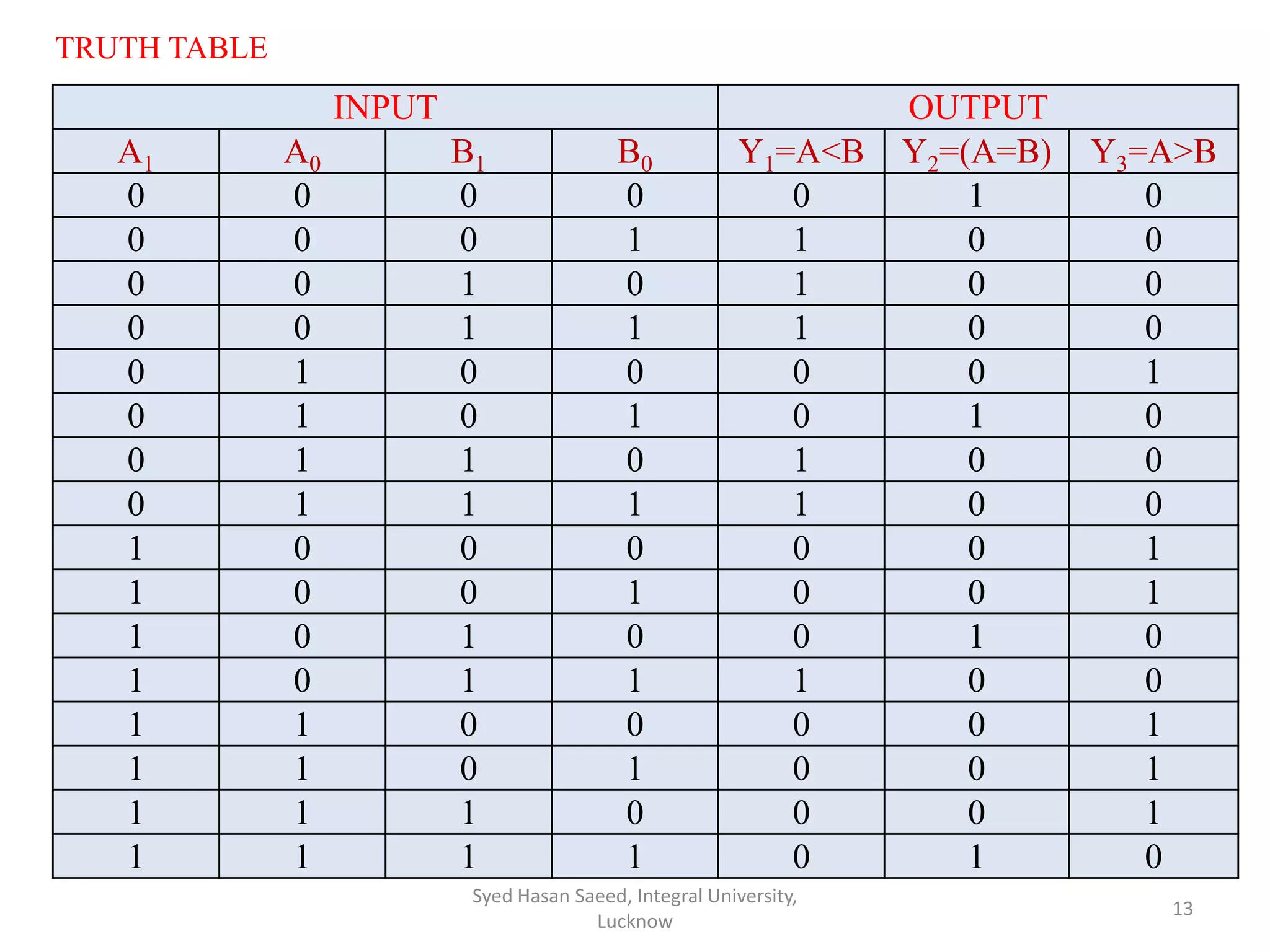
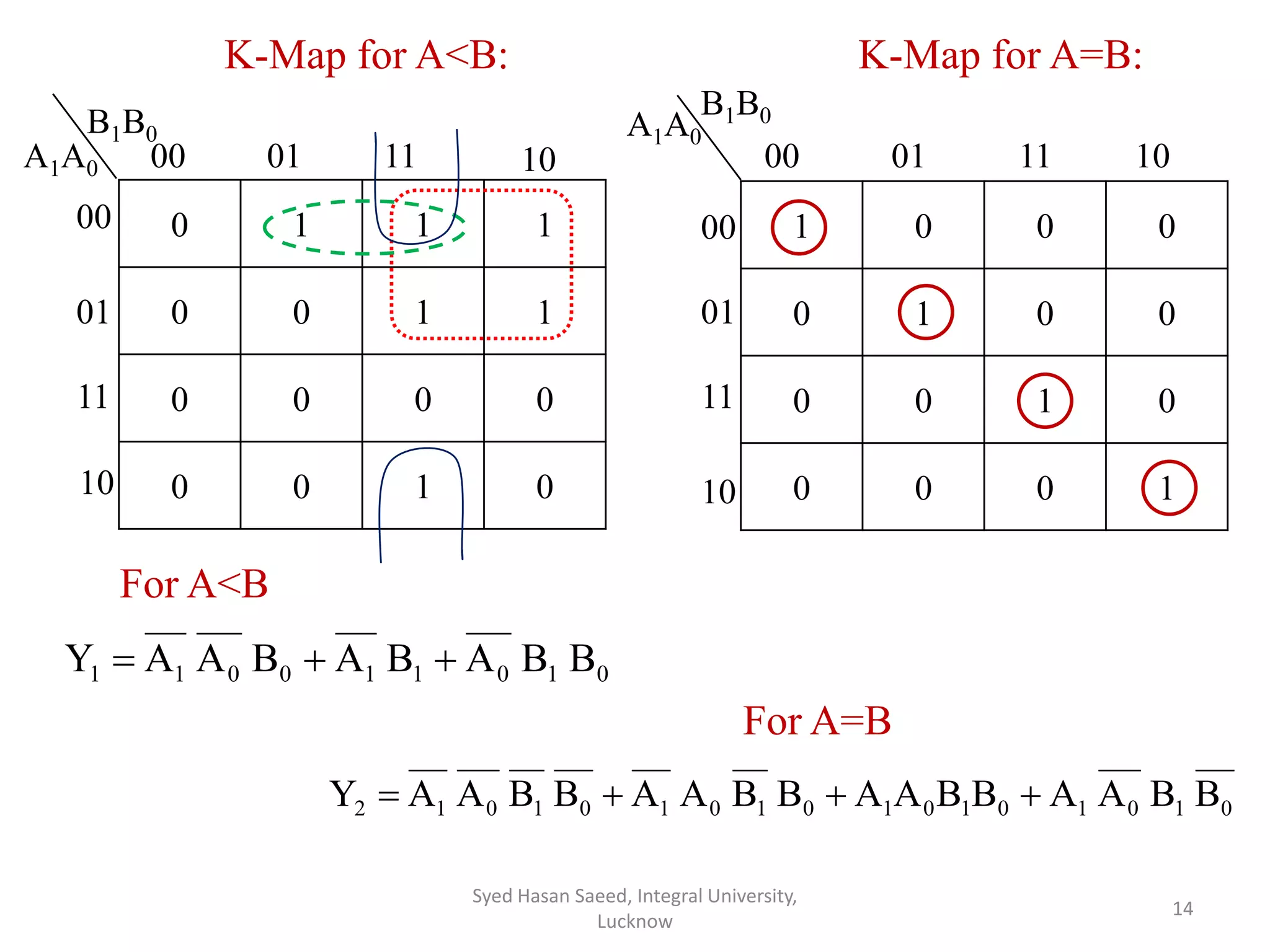
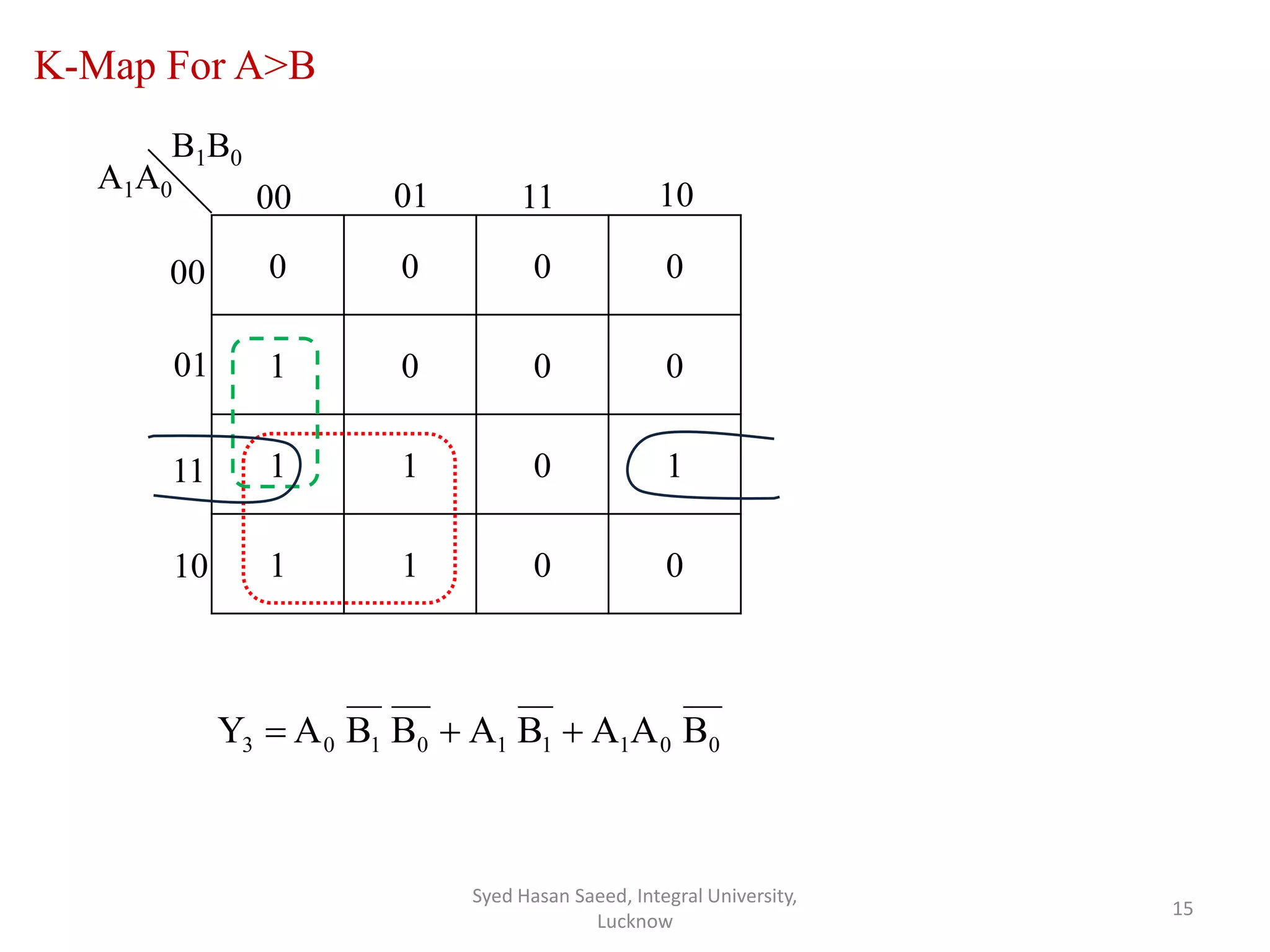
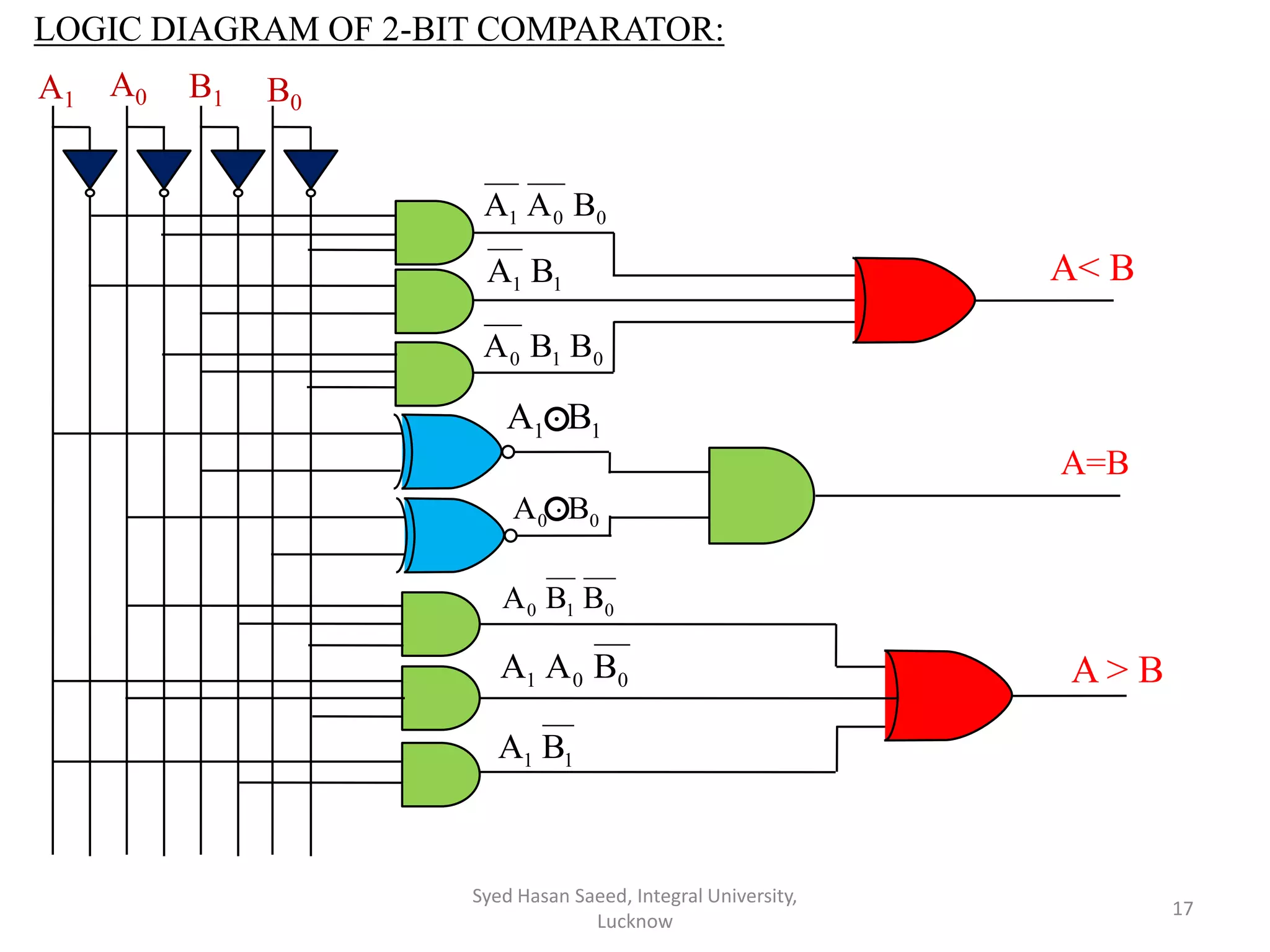
The document discusses magnitude comparators, which are digital circuits used to compare the values of two binary numbers. There are two types: identity comparators and magnitude comparators. Magnitude comparators have three outputs - A>B, A=B, and A<B to indicate the relationship between the inputs. The document then discusses the design and implementation of 1-bit and 2-bit magnitude comparators using logic gates like AND and XOR. Truth tables and K-maps are used to derive the logic expressions for the three outputs in each case. Finally, the logic diagram of a 2-bit magnitude comparator is presented.

1. MAGNITUDE COMPARATOR
Syed Hasan Saeed, Integral University,
Lucknow
2

2. MAGNITUDE COMPARATOR: DIGITAL COMPARATOR
• It is a combinational logic circuit.
• Digital Comparator is used to compare the value of two binary
digits.
• There are two types of digital comparator (i) Identity Comparator
(ii) Magnitude Comparator.
• IDENTITY COMPARATOR: This comparator has only one output
terminal for when A=B, either A=B=1 (High) or A=B=0 (Low)
• MAGNITUDE COMPARATOR: This Comparator has three output
terminals namely A>B, A=B, A<B. Depending on the result of
comparison, one of these output will be high (1)
• Block Diagram of Magnitude Comparator is shown in Fig. 1
Syed Hasan Saeed, Integral University,
Lucknow
3

3. BLOCK DIAGRAM OF MAGNITUDE COMPARATOR
Syed Hasan Saeed, Integral University,
Lucknow
4
n- Bit Digital Comparator
A
n-Bit
B
n-Bit
A<B A=B A>B
Fig. 1

4. 1- Bit Magnitude Comparator:
• This magnitude comparator has two inputs A and B and three
outputs A<B, A=B and A>B.
• This magnitude comparator compares the two numbers of single
bits.
• Truth Table of 1-Bit Comparator
Syed Hasan Saeed, Integral University,
Lucknow
5
INPUTS OUTPUTS
A B Y1 (A<B) Y2 (A=B) Y3 (A>B)
0 0 0 1 0
0 1 1 0 0
1 0 0 0 1
1 1 0 1 0

5. K-Maps For All Three Outputs :
Syed Hasan Saeed, Integral University,
Lucknow
6
A
B
0 1
0
1
0
0 0
1
B B
A
A
B
A
Y1 
K-Map for Y1 : A<B

6. K-Maps For All Three Outputs :
Syed Hasan Saeed, Integral University,
Lucknow
7
A
B
0 1
0
1
0
0 0
1
B B
A
A
B
A
Y1 
K-Map for Y1 : A<B
A
B
0 1
0
1
1
0 1
0
B B
A
A
AB
B
A
Y2 

K-Map for Y2 : A=B

7. K-Maps For All Three Outputs :
Syed Hasan Saeed, Integral University,
Lucknow
8
A
B
0 1
0
1
0
0 0
1
B B
A
A
B
A
Y1 
K-Map for Y1 : A<B
A
B
0 1
0
1
1
0 1
0
B B
A
A
AB
B
A
Y2 

K-Map for Y2 : A=B
A 0 1
0
1
0
1
0
B
B
A
A
B
0
B
A
Y3 
K-Map for Y2 : A>B

8. Realization of One Bit Comparator
Syed Hasan Saeed, Integral University,
Lucknow
9
B
A
B
A
Y1 

A
B
AB
B
A
AB
B
A
Y2 

B
A
Y3 
B
A 
B
A 
B
A
Y1 
AB
B
A
Y2 

B
A
Y3 

9. Realization of by Using AND , EX-NOR gates
Syed Hasan Saeed, Integral University,
Lucknow
10
B
A
B
A
Y1 

B
A
B
A
Y2



B
A
Y3 
B
A 
A
B

10. 2-Bit Comparator:
• A comparator which is used to compare two binary numbers each of two
bits is called a 2-bit magnitude comparator.
• Fig. 2 shows the block diagram of 2-Bit magnitude comparator.
• It has four inputs and three outputs.
• Inputs are A0 ,A1,B0 and B1 and Outputs are Y1, Y2 and Y3
Syed Hasan Saeed, Integral University,
Lucknow
11
A0
A1
B1
B0
Y1
Y2
Y3
2-Bit Comparator
Fig. 2
A
B
Input Output

11. GREATER THAN (A>B)
LESS THAN (A<B)
Similarly,
1. If A1= B1=1 and A0= 0, B0=1, then A<B
2. If A1= B1= 0 and A0= 0, B0=1 then A<B
Syed Hasan Saeed, Integral University,
Lucknow
12
A1 A0 B1 B0
1 0 0 1
1 1 1 0
0 1 0 0
1. If A1= 1 and B1= 0 then A>B
2. If A1 and B1 are same, i.e A1=B1=1 or A1=B1=0 and A0=1, B0=0
then A>B

12. INPUT OUTPUT
A1 A0 B1 B0 Y1=A<B Y2=(A=B) Y3=A>B
0 0 0 0 0 1 0
0 0 0 1 1 0 0
0 0 1 0 1 0 0
0 0 1 1 1 0 0
0 1 0 0 0 0 1
0 1 0 1 0 1 0
0 1 1 0 1 0 0
0 1 1 1 1 0 0
1 0 0 0 0 0 1
1 0 0 1 0 0 1
1 0 1 0 0 1 0
1 0 1 1 1 0 0
1 1 0 0 0 0 1
1 1 0 1 0 0 1
1 1 1 0 0 0 1
1 1 1 1 0 1 0
Syed Hasan Saeed, Integral University,
Lucknow
13
TRUTH TABLE

13. K-Map for A<B: K-Map for A=B:
Syed Hasan Saeed, Integral University,
Lucknow
14
0 1 1 1
0 0 1 1
0 0 0 0
0 0 1 0
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
00 01
00
01
11
10
11 10 00 01 11 10
00
01
11
10
A1A0
A1A0
B1B0
B1B0
For A<B
For A=B
0
1
0
1
1
0
0
1
1 B
B
A
B
A
B
A
A
Y 


0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
2 B
B
A
A
B
B
A
A
B
B
A
A
B
B
A
A
Y 




14. K-Map For A>B
Syed Hasan Saeed, Integral University,
Lucknow
15
0 0 0 0
1 0 0 0
1 1 0 1
1 1 0 0
00 01 11 10
00
01
11
10
A1A0
B1B0
0
0
1
1
1
0
1
0
3 B
A
A
B
A
B
B
A
Y 



15. For A=B From K-Map
Syed Hasan Saeed, Integral University,
Lucknow
16
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
2 B
B
A
A
B
B
A
A
B
B
A
A
B
B
A
A
Y 



)
B
(A
)
B
A
(
Y
)
B
A
B
A
(
)
B
A
B
A
(
Y
)
B
A
B
A
(
B
A
)
B
A
B
A
(
B
A
Y
0
0
1
1
2
0
0
0
0
1
1
1
1
2
1
1
1
1
0
0
1
1
1
1
0
0
2











16. LOGIC DIAGRAM OF 2-BIT COMPARATOR:
Syed Hasan Saeed, Integral University,
Lucknow
17
A1 A0 B1 B0
A< B
A=B
A > B
0
0
1 B
A
A
1
1 B
A
0
1
0 B
B
A
1
1 B
A
0
0
1 B
A
A
0
1
0 B
B
A
1
1 B
A 
0
0 B
A 

17. THANK YOU
Syed Hasan Saeed, Integral University,
Lucknow
18

18. Quick Quiz (Poll 1)
• If two numbers are not equal then binary
variable will be ____________
a) 0
b) 1
c) A
d) B

19. Quick Quiz (Poll 2)
• Comparators are used in ____________
a) Memory
b) CPU
c) Motherboard
d) Hard drive