Magical

魔法陣
原案 : fura2
解答 : fura2
解説 : fura2

問題概要
● こんな感じの魔法陣の青い部分の面積を求めよ

解法
● 二種類あります

解法 1
● まず、多角形が三角形のときを考える

● f(r) := ( 三角形と半径 r の円の共通部分の面積 )
とする
f(r)

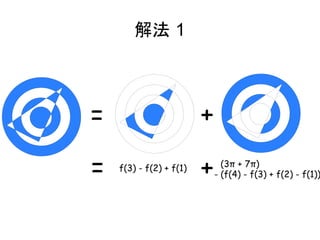
解法 1

= +
= f(3) - f(2) + f(1)
+ (3π + 7π)
- (f(4) - f(3) + f(2) - f(1))

解法 1
● 一般の単純多角形のとき

●
多角形を三角形分割すれば、三角形の場合に帰
着できる
– サイズが小さいので、三角形分割は計算量が悪い方法
でやってもいい。O(n3 log n) くらいまでなら何でもOK
– 一応、理論上は O(n) でできるらしい

解法 2
● 適当な点 c を中心として、偏角方向に平面走査す
る
– イベント点は、多角形の頂点、円と多角形の交点

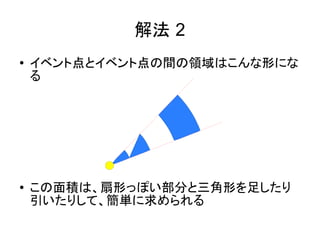
解法 2
● イベント点とイベント点の間の領域はこんな形にな
る

● この面積は、扇形っぽい部分と三角形を足したり
引いたりして、簡単に求められる

解法 2
● 中心 c の選び方について
– 扇形っぽい部分の面積を求めやすくするため、c は半
径 1 の円の内部にとるのがいい
– c を原点とすると、扇形っぽい部分が本当に扇形になる
けど、多角形の頂点が原点にあるケースがコーナー
ケースになりうるので注意

提出状況
● AC Rate
– 0 % (0/2)

● First Acceptance
– Onsite: なし
– All: なし

Recommended